Digitale Werkzeuge in der Schule/Basiswissen Analysis/Steckbriefaufgaben: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 360: | Zeile 360: | ||
1. Gleichung I * (-2) von Gleichung II abziehen. | 1. Gleichung I * (-2) von Gleichung II abziehen. | ||
2. Gleichung I *(4) von Gleichung III abziehen. | 2. Gleichung I * (4) von Gleichung III abziehen. | ||
3. Gleichung II * (\frac{46}{31}) von Gleichung III abziehen. | 3. Gleichung II * (<math> \frac{46}{31} </math>) von Gleichung III abziehen. | ||
4. z aus der Gleichung III berechnen. | 4. z aus der Gleichung III berechnen. | ||
| Zeile 393: | Zeile 393: | ||
{{Lösung versteckt| Die Matrix sollte in eine obere rechte Dreiecksmatrix umgeschrieben werden. | Tipp 2| Tipp 2 ausblenden}} | {{Lösung versteckt| Die Matrix sollte in eine obere rechte Dreiecksmatrix umgeschrieben werden. | Tipp 2| Tipp 2 ausblenden}} | ||
{{Lösung versteckt| <math> x=\frac{7}{2}</math>,<math>y=-7</math>, <math> z=1 </math>, <math> v=\frac{5}{2} </math> |Lösung |Lösung ausblenden}} | {{Lösung versteckt| | ||
1.Gleichung I * (-2) von Gleichung II abziehen. | |||
2.Gleichung I * (-3) von Gleichung III abziehen. | |||
3. Gleichung II * (<math> \frac{-16}{3} </math>) von Gleichung III abziehen. | |||
4. Gleichung II * (<math> \frac{2}{3} </math>) zu Gleichung IV addieren. | |||
5. Gleichung III * (<math> \frac{1}{13} </math>) von Gleichung IV abziehen. | |||
6. v aus Gleichung IV berechnen. | |||
7. v in Gleichung III einsetzen und nach z auflösen. | |||
8. v und z in Gleichung II einsetzten und nach y auflösen. | |||
9. v,z und y in Gleichung I einsetzen und nach x auflösen. | |||
Endgültige Lösung: | |||
<math> x=\frac{7}{2}</math>,<math>y=-7</math>, <math> z=1 </math>, <math> v=\frac{5}{2} </math> |Lösung |Lösung ausblenden}} | |||
|Farbe= #F19E4F|3= Arbeitsmethode}} | |Farbe= #F19E4F|3= Arbeitsmethode}} | ||
Version vom 25. Mai 2020, 18:56 Uhr
Das Einsetzungsverfahren
Aufgaben zum Einsetzungsverfahren
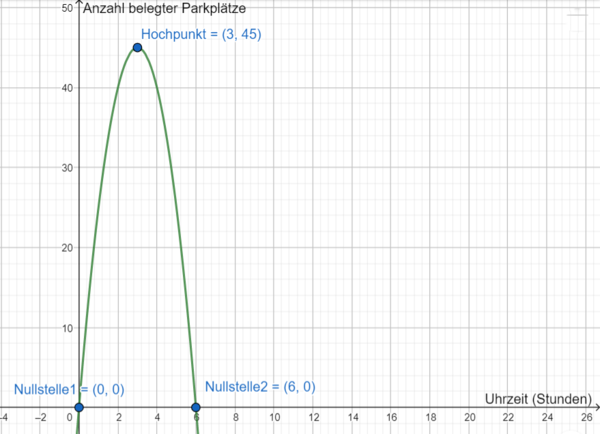
Quadratische Funktionen im Sachzusammenhang
Das Gauß-Verfahren
Aufgaben zum Gauß-Verfahren
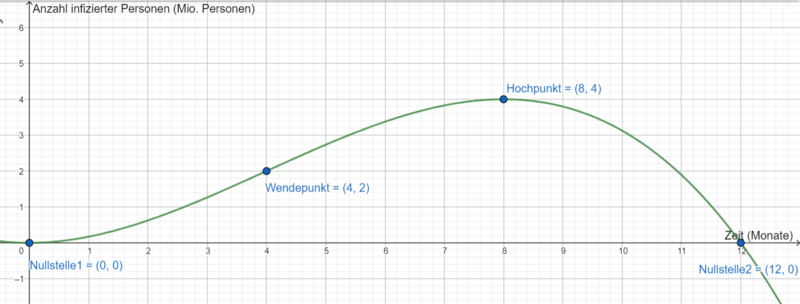
Kubische Funktionen im Sachzusammenhang