Digitale Werkzeuge in der Schule/Basiswissen Analysis/Steckbriefaufgaben

Info

In diesem Lernpfadkapitel lernst du Steckbriefaufgaben kennen. In Steckbriefaufgaben geht es darum, aus den Eigenschaften einer Funktion deren Funktionsterm und Funktionsgraphen herzuleiten.

• In Aufgaben, die orange gefärbt sind, kannst du Gelerntes wiederholen und vertiefen.
• Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit.
• Und Aufgaben mit grüner Hinterlegung sind Knobelaufgaben.
• Aufgaben, die mit einem ⭐ gekennzeichnet sind, sind nur für den LK gedacht.

Damit übst du das Modellieren und Mathematisieren , indem du mithilfe mathematischer Kenntnisse und Fertigkeiten Lösungen innerhalb mathematischer Modelle erarbeitest. Dazu ist das Lösen von Gleichungssystemen mit mehr als einer Variablen notwendig. Du stellst lineare Gleichungssysteme in Matrix-Vektor-Schreibweise dar, löst sie mithilfe geeigneter Verfahren und interpretierst ihre Lösungsmenge.

Wir empfehlen dir, dich bereits mit den Eigenschaften von Funktionen und der lokalen Änderungsrate beschäftigt zu haben, wenn du mit dieser Seite beginnst.

Das Einsetzungsverfahren

Das Einsetzungsverfahren

Das Einsetzungsverfahren kannst du verwenden, um ein Gleichungssystem mit zwei Variablen zu lösen. Dabei versuchst du zuerst eine Variable allein auf eine Seite zu bringen und diese Gleichung dann in die zweite Gleichung einzusetzen.

Schau dir folgendes Gleichungssystem an:

$\begin{array}{rlll} &I\quad& &3x& + &5y& &=& &58&\\ &II\quad& &x& + &2& &=& &y& \\ \end{array}$

Die Gleichung $II$ ist bereits nach der Variable $y$ aufgelöst. Die linke Seite der Gleichung fügen wir nun statt $y$ in die die Gleichung $I$ ein. Das sieht folgendermaßen aus:

$3x + 5 \cdot (x + 2) = 58$

1. Wir vereinfachen

$3x + 5x + 10 = 58$

2. Und stellen nach $x$ um

$8x = 48$

3. Dann teilen wir durch den Vorfaktor, hier 8 und es ergibt sich

$x = 6$

4. Das können wir nun in eine der beiden Gleichungen einsetzen und nach $y$ umstellen. Gleichung $II$ eignet sich dafür natürlich am besten. Es gilt:

$\begin{array}{rlll} &II\quad&&& x + 2 &=& y &\mid x = 6 \, \textrm{einsetzen} \\ &&&\Rightarrow& 6 + 2 &=& y \\ &&&\Rightarrow& y &=& 8 \\ \end{array}$

Du verwendest dieses Verfahren bei Gleichungssystemen mit 2 Variablen. Dabei stellst du die eine Gleichung nach einer Variable um und setzt diese dann in die andere Gleichung ein. Nun kannst du vorgehen wie bei einer Gleichung mit nur einer Variable.

Aufgaben zum Einsetzungsverfahren

Gleichungssysteme mit dem Einsetzungsverfahren lösen

Aufgabe a) ist etwas einfacher als Aufgabe b).

a)

$\begin{array}{rlll} &I\quad& &7x& + &3y& &=& &50&\\ &II\quad& && &18y& &=& &6& \\ \end{array}$

$x=7$,$y=\frac{1}{3}$

b)

$\begin{array}{rlll} &I\quad& &3x& + &6y& &=& &6&\\ &II\quad& &-2x& + &12y& &=& &0& \\ \end{array}$

Stelle I nach $y$ um und setzte diese in II ein, um $y$ zu eliminieren.

$x=\frac{3}{2}$,$y=\frac{1}{4}$

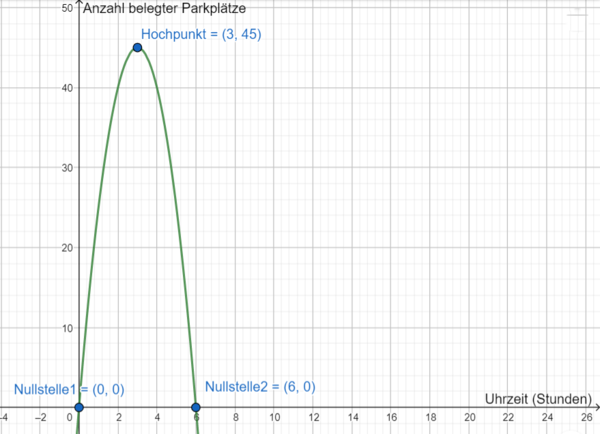
Quadratische Funktionen im Sachzusammenhang

Elternsprechtag

Jedes halbe Jahr veranstaltet eine Schule einen Elternsprechtag von 12 Uhr bis 18 Uhr. Den Eltern stehen auf dem Lehrerparkplatz aber nur eine begrenzte Anzahl an Parkplätzen zur Verfügung, sodass die Schulleitung rechtzeitig entscheiden muss, ob noch weitere Parkplätze angemietet werden müssen. Sie geht davon aus, dass der erste Parkplatz erst nach Beginn des Elternsprechtages belegt wird und spätestens um 18 Uhr das letzte Auto den Parkplatz verlassen hat. Diesen Elternsprechtag stehen den Eltern 50 Parkplätze zur Verfügung. Eine Zählung um 13 Uhr ergibt, dass bereits die Hälfte der zur Verfügung stehenden Parkplätze belegt ist.

a) Die Anzahl belegter Parkplätze lässt sich in Abhängigkeit zur Uhrzeit (mit $t$ in Stunden, wobei $t = 0$ 12 Uhr repräsentiert) durch eine quadratische Funktion der Form $f(t) = at^2 + bt + c$ beschreiben. Löse zunächst den unteren Lückentext.

b) Stelle mit Hilfe von Aufgabe a) die Gleichung von $f$ auf. Mit unterem Applet kannst du dein Ergebnis selbstständig überprüfen.

$f(t) = -5t^2 + 30t$

$\begin{array}{rlll} f(t) &=& at^2 + bt + c \\ \end{array}$



$\begin{array}{rlll} &&f(0) &=& 0 \\ &\Leftrightarrow& a \cdot 0^2 + b \cdot 0 + c &=& 0 \\ &\Leftrightarrow& c &=& 0 \\ \end{array}$



$\Rightarrow f(t) = at^2 + bt$



$\begin{array}{rlll} &&f(1) &=& 25 \\ &\Leftrightarrow& a \cdot 1^2 + b \cdot 1 &=& 25 \\ &\Leftrightarrow& a + b &=& 25 \\ \end{array}$



$\begin{array}{rlll} &&f(6) &=& 0 \\ &\Leftrightarrow& a \cdot 6^2 + b \cdot 6 &=& 0 \\ &\Leftrightarrow& 36a + 6b &=& 0 \\ \end{array}$





Insgesamt erhalten wir also folgendes Gleichungssystem:

$\begin{array}{rlll} &I\quad& a + b &=& 25 \\ &II\quad& 36a + 6b &=& 0 \\ \end{array}$

Dieses Gleichungssystem lösen wir mit dem Einsetzungsverfahren:

Als erstes stellen wir Gleichung $I$ nach $a$ um und erhalten

$\begin{array}{rlll} &I\quad& a = 25 - b \\ \end{array}$

Setzen wir diese (umgeformte) Gleichung $I$ in Gleichung $II$ ein, erhalten wir

$\begin{array}{rlll} &II\quad&&& 36a + 6b &=& 0 &\mid a = 25 - b \, \textrm{einsetzen} \\ &&&\Rightarrow& 36 \cdot (25 - b) + 6b &=& 0 &\mid \textrm{Ausmultiplizieren} \\ &&&\Rightarrow& 900 - 36b + 6b &=& 0 \\ &&&\Rightarrow& 900 - 30b &=& 0 &\mid + 30b \\ &&&\Rightarrow& 30b &=& 900 &\mid : 30 \\ &&&\Rightarrow& b &=& 30 \\ \end{array}$

Setzen wir $b = 30$ in die (umgeformte) Gleichung $I$ ein, erhalten wir

$\begin{array}{rlll} &I&&& a &=& 25 - b &\mid b = 30 \, \textrm{einsetzen} \\ &&&\Rightarrow& a &=& 25 - 30 \\ &&&\Rightarrow& a &=& -5 \\ \end{array}$

und damit insgesamt

$f(t) = -5t^2 + 30t$

c) Entscheide, ob die 50 Parkplätze für die gesamte Dauer des Elternsprechtages ausreichend sind oder zusätzliche Parkplätze angemietet werden müssen.

Damit die Parkplätze ausreichen, dürfen maximal 50 Parkplätze zu einer bestimmten Uhrzeit belegt sein. Hat die Funktion einen Hochpunkt mit einem Funktionswert kleiner gleich 50, so ist sie nirgendwo größer als dort.

$\begin{array}{rlll} &\textrm{notwendige} \, \textrm{Bedingung:}& f'(t) &=& 0 \\ &\textrm{hinreichende} \, \textrm{Bedingung:}& f''(t) &<& 0 \\ \end{array}$

Der Graph der Funktion $f$ hat den Hochpunkt $(3 | 45)$. Die maximale Anzahl belegter Parkplätze ist also um 15 Uhr nachzuweisen. Zu der Zeit sind 45 Parkplätze belegt, sodass die vorhandenen 50 Parkplätze ausreichen.

$\begin{array}{rlll} f(t) &=& -5t^2 + 30t \\ f'(t) &=& -10t + 30 \\ f''(t) &=& -10 \\ \end{array}$

$\begin{array}{rlll} \textrm{Notwendige Bedingung:} && f'(t) &=& 0 \\ &\Leftrightarrow& -10t + 30 &=& 0 &\mid + 10t\\ &\Leftrightarrow& 10t &=& 30 &\mid : 10 \\ &\Leftrightarrow& t &=& 3 \\ \end{array}$



$\begin{array}{rlll} \textrm{Hinreichende Bedingung:} &&f'(3) &=& 0 &&\textrm{und} \\ &&f''(3) &=& -10 &<& 0 \end{array}$

$f(3)=-5 \cdot 3^2 + 30 \cdot 3 = 45$

d) Skizziere nun den Graphen von $f$ anhand der Informationen auf einem Blatt. Beachte hierbei die geeignete Beschriftung der Koordinatenachsen. Für welchen Zeitraum ist dieser Graph als mathematische Modellierung der Parkplatzsituation geeignet?

Da die Funktionswerte von $f$ für $t < 0$ und $t > 6$ negativ sind, ist der Graph nur für $0 \leq t \leq 6$ als mathematische Modellierung der Parkplatzsituation geeignet.

Das Gauß-Verfahren

Das Gauß-Verfahren

Das Gauß-Verfahren verwendest du bei Gleichungssystemen mit 2 oder mehr Variablen. Dabei versuchst du die Gleichungen so zu vereinfachen, dass eine obere Dreiecksmatix entsteht.

Schaue dir folgende Gleichungen an:

$\begin{array}{rlll} &I\quad& &3x& + &5y& + &4z& &=& &6&\\ &II\quad& &2x& + &1y& + &7z& &=& &15& \\ &III\quad& &1x& + &2y& + &3z& &=& &5& \\ \end{array}$

1. Um die $x$-Variable in Gleichung $II$ zu eliminieren rechnen wir $II + (-2) \cdot III$:

$\begin{array}{rlll} &I\quad& &3x& + &5y& + &4z& &=& &6&\\ &II\quad& && - &3y& + &1z& &=& &5& \\ &III\quad& &1x& + &2y& + &3z& &=& &5& \\ \end{array}$

In Matrix-Vektor-Schreibweise:

$\begin{pmatrix} 3 & 5 & 4& 6 \\ 0 & -3 & 1 & 15 \\ 1 & 2 & 3 & 5\end{pmatrix}$

2. Um die $x$-Variable in Gleichung $III$ zu eliminieren rechnen wir $III \cdot (-3) + I$:

$\begin{array}{rlll} &I\quad& &3x& + &5y& + &4z& &=& &6&\\ &II\quad& && - &3y& + &1z& &=& &5& \\ &III\quad& && - &1y& - &5z& &=& &-9& \\ \end{array}$

In Matrix-Vektor-Schreibweise:

$\begin{pmatrix} 3 & 5 & 4& 6 \\ 0 & -3 & 1 & 15 \\ 0 & -1 & -5 & -9\end{pmatrix}$

3. Nun soll auch die $y$-Variable in Gleichung $III$ eliminiert werden. Dazu rechnen wir $III \cdot (-3) + II$

Unsere Gleichungen sehen nun folgendermaßen aus:

$\begin{array}{rlll} &I\quad& &3x& + &5y& + &4z& &=& &6&\\ &II\quad& && - &3y& + &1z& &=& &5& \\ &III\quad& && && + &16z& &=& &32& \\ \end{array}$

In Matrix-Vektor-Schreibweise:

$\begin{pmatrix} 3 & 5 & 4& 6 \\ 0 & -3 & 1 & 15 \\ 0 & 0 & 16 & 32\end{pmatrix}$

Wir können Gleichung $III$ nun nach $z$ auflösen. Dann setzen wir den $z$-Wert in Gleichung $II$ ein und lösen nach $y$ auf. Zuletzt setzten wir jeweils den berechneten $y$- und $z$-Wert in Gleichung $I$ ein und lösen nach $x$ auf. Wir erhalten so unsere dritte Variable.

Es folgt also:

$z=2$, $y=-1$, $x=1$

Du verwendest dieses Verfahren bei Gleichungssystemen mit 2 oder mehr Variablen. Dabei stellst du die Gleichungen so um, das in einer Gleichung nur eine Variable, in der zweiten Gleichung zwei Variablen und in der dritten Gleichung alle drei Variablen vorkommen. Das bezeichnet man auch als obere Dreiecksmatrix. Nun kannst du mit der ersten Gleichung so vorgehen wie bei einer Gleichung mit nur einer Variable und die Lösung dann in die zweite Gleichung einsetzen. Die Lösung dieser Gleichung setzt du dann in die letzte Gleichung ein. Bei vier Gleichungen mit vier Variablen gehst du analog vor.

Aufgaben zum Gauß-Verfahren

Gleichungssysteme mit dem Gauß-Verfahren lösen

Die Schwierigkeit der Aufgaben steigt von oben nach unten.

a)

$\begin{array}{rlll} &I\quad& &1x& + &12y& + &6z& &=& &-2&\\ &II\quad& &-2x& + &7y& + &18z& &=& &24,5& \\ &III\quad& &4x& + &2y& + &24z& &=& &-31& \\ \end{array}$

Schreibe die Gleichungen in die Matrix-Vektor-Schreibweise um.

Eliminiere zuerst die $x$-Variable in der zweiten Zeile.

Deine Matrix sollte in folgende Form umgeschrieben werden. $\begin{pmatrix} a & b & c & d \\ 0 & e & f & g \\ 0 & 0 & h & i \end{pmatrix}$.

$x=-9$,$y=7$, $z=\frac{1}{6}$

b) ⭐

$\begin{array}{rlll} &I\quad& &3x& + &4y& - &5z& + &6v& &=& &-7,5&\\ &II\quad& &6x& + &5y& - &6z& + &5v& &=& &-7,5& \\ &III\quad& &9x& - &4y& + &2z& + &3v& &=& &69& \\ &IV\quad& && &2y& - &3z& + &1v& &=& &-14,5& \end{array}$

Schreibe die Gleichungen in die Matrix-Vektor-Schreibweise um.

Eliminiere zuerst den $x$-Wert in Gleichung $II$.

Die Matrix sollte in eine obere rechte Dreiecksmatrix umgeschrieben werden.

$x=\frac{7}{2}$,$y=-7$, $z=1$, $v=\frac{5}{2}$

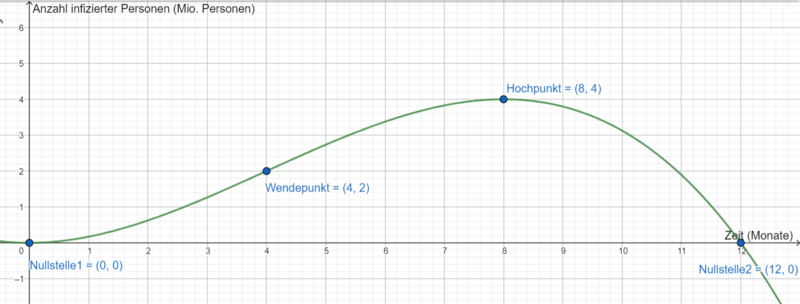
Kubische Funktionen im Sachzusammenhang

Virusinfektion

Anmerkung: alle unteren Angaben sind frei erfunden

Im Januar befällt ein neuartiges Virus Deutschland. Mittlerweile ist es Oktober und du suchst im Internet nach Informationen über die Infektionszahlen. Dort triffst du auf folgende Informationen:

• Im Dezember des Vorjahres befinden sich noch keine infizierten Personen in Deutschland
• Im April leben 2.000.000 infizierte Personen in Deutschland
• Im August leben 4.000.000 infizierte Personen in Deutschland
• Durch entsprechende Maßnahmen ist die Zahl infizierter Personen ab August rückläufig

a) Die Anzahl infizierter Personen lässt sich durch eine kubische Funktion (Funktion dritten Grades) der Form $f(t) = at^3 + bt^2 + ct + d$ beschreiben. Löse zunächst unteren Lückentext.

b) Stelle mit Hilfe von Aufgabe a) die Gleichung von $f$ auf. Mit unterem Applet kannst du dein Ergebnis selbstständig überprüfen.

$f(t) = -\frac{1}{64} t^3 + \frac{3}{16} t^2 = \frac{1}{64} (-t^3 + 12t^2)$

$\begin{array}{rlll} f(t) &=& at^3 + bt^2 + ct + d \\ f'(t) &=& 3at^2 + 2bt + c \\ \end{array}$



$\begin{array}{rlll} &&f(0) &=& 0 \\ &\Leftrightarrow& a \cdot 0^3 + b \cdot 0^2 + c \cdot 0 + d &=& 0 \\ &\Leftrightarrow& d &=& 0 \\ \end{array}$



$\Rightarrow f(t) = at^3 + bt^2 + ct$



$\begin{array}{rlll} &&f(4) &=& 2 \\ &\Leftrightarrow& a \cdot 4^3 + b \cdot 4^2 + c \cdot 4 &=& 2 \\ &\Leftrightarrow& 64a + 16b + 4c &=& 2 \\ \end{array}$



$\begin{array}{rlll} &&f(8) &=& 4 \\ &\Leftrightarrow& a \cdot 8^3 + b \cdot 8^2 + c \cdot 8 &=& 4 \\ &\Leftrightarrow& 512a + 64b + 8c &=& 4 \\ \end{array}$



$\begin{array}{rlll} &&f'(8) &=& 0 \\ &\Leftrightarrow& 3a \cdot 8^2 + 2b \cdot 8 + c &=& 0 \\ &\Leftrightarrow& 192a + 16b + c &=& 0 \\ \end{array}$





Insgesamt erhalten wir also folgendes Gleichungssystem:

$\begin{array}{rlll} &I\quad& &64a& + &16b& + &4c& &=& &2& \\ &II\quad& &512a& + &64b& + &8c& &=& &4& \\ &III\quad& &192a& + &16b& + &1c& &=& &0& \\ \end{array}$

Dieses Gleichungssystem lösen wir mit dem Gauß-Verfahren:

$II - 8 \cdot I$

$\begin{array}{rlll} &I\quad& &64a& + &16b& + &4c& &=& &2& \\ &II\quad& && - &64b& - &24c& &=& &-12& \\ &III\quad& &192a& + &16b& + &1c& &=& &0& \\ \end{array}$



$III - 3 \cdot I$

$\begin{array}{rlll} &I\quad& &64a& + &16b& + &4c& &=& &2& \\ &II\quad& && - &64b& - &24c& &=& &-12& \\ &III\quad& && - &32b& - &11c& &=& &-6& \\ \end{array}$



$III - \frac{1}{2} \cdot II$

$\begin{array}{rlll} &I\quad& &64a& + &16b& + &4c& &=& &2& \\ &II\quad& && - &64b& - &24c& &=& &-12& \\ &III\quad& && && &21c& &=& &0& \\ \end{array}$



Gleichung $III$ liefert uns nun

$\begin{array}{rlll} &III\quad&&& 21c &=& 0 &\mid : 21 \\ &&&\Rightarrow& c &=& 0 \\ \end{array}$

Setzen wir $c = 0$ in Gleichung $II$ ein, erhalten wir

$\begin{array}{rlll} &II\quad&&& -64b + 24c &=& -12 &\mid c = 0 \, \textrm{einsetzen} \\ &&&\Rightarrow& -64b + 24 \cdot 0 &=& -12 \\ &&&\Rightarrow& -64b &=& -12 &\mid : (-64) \\ &&&\Rightarrow& b &=& \frac{3}{16} \\ \end{array}$

Setzen wir $c = 0$ und $b = \frac{3}{16}$ in Gleichung $I$ ein, erhalten wir

$\begin{array}{rlll} &I\quad&&& 64a + 16b + 4c &=& 2 &\mid c = 0 \, \textrm{und} \, b = \frac{3}{16} \, \textrm{einsetzen}\\ &&&\Rightarrow& 64a + 16 \cdot \frac{3}{16} + 4 \cdot 0 &=& 2 \\ &&&\Rightarrow& 64a + 3 &=& 2 &\mid -3 \\ &&&\Rightarrow& 64a &=& -1 &\mid : 64 \\ &&&\Rightarrow& a &=& -\frac{1}{64} \\ \end{array}$



und damit insgesamt

$f(t) = -\frac{1}{64} t^3 + \frac{3}{16} t^2 = \frac{1}{64} (-t^3 + 12t^2)$

c) Wissenschaftler behaupten, dass die milden Temperaturen im Frühling dafür sorgen, dass sich der temperaturempfindliche Virus optimal ausbreiten kann und deshalb die stärkste Zunahme infizierter Personen im Frühling nachzuweisen ist. Prüfe diese Behauptung anhand der Informationen.

Der Wendepunkt ist der Punkt der stärksten Zunahme (oder stärksten Abnahme) des Funktionsgraphen, der an dieser Stelle sein Krümmungsverhalten ändert.

$\begin{array}{rlll} &\textrm{notwendige} \, \textrm{Bedingung:}& f''(t) &=& 0 \\ &\textrm{hinreichende} \, \textrm{Bedingung:}& f'''(t) &\neq& 0 \\ \end{array}$

Der Graph der Funktion $f$ hat einen Wendepunkt bei $t = 4$. Die stärkste Zunahme infizierter Personen ist also im April (bzw. im Frühling) nachzuweisen. Die Behauptung ist demnach richtig.

$\begin{array}{rlll} f(t) &=& -\frac{1}{64} t^3 + \frac{3}{16} t^2 \\ f'(t) &=& -\frac{3}{64} t^2 + \frac{3}{8} t \\ f''(t) &=& -\frac{3}{32} t + \frac{3}{8} \\ f'''(t) &=& -\frac{3}{32} \\ \end{array}$

$\begin{array}{rlll} \textrm{Notwendige} \, \textrm{Bedingung:} && f''(t) &=& 0 \\ &\Leftrightarrow& -\frac{3}{32} t + \frac{3}{8} &=& 0 &\mid +\frac{3}{32} t\\ &\Leftrightarrow& \frac{3}{32} t &=& \frac{3}{8} &\mid :\frac{3}{32} \\ &\Leftrightarrow& t &=& 4 \\ \end{array}$

$\begin{array}{rlll} \textrm{Hinreichende} \, \textrm{Bedingung:} &&f''(4) &=& 0 &&\textrm{und} \\ &&f'''(4) &=& -\frac{3}{32} &\neq& 0 \end{array}$

d) Skizziere nun den Graphen von $f$ anhand der Informationen auf einem Blatt. Beachte hierbei die geeignete Beschriftung der Koordinatenachsen. Für welchen Zeitraum ist dieser Graph als mathematische Modellierung der Virusinfektion geeignet?

Da die Funktionswerte von $f$ für $t > 12$ negativ sind, ist der Graph nur für $0 \leq t \leq 12$ als mathematische Modellierung der Virusinfektion geeignet. Inwiefern der Graph für das vorherige Jahr geeignet ist, lässt sich anhand der Informationen nicht eindeutig feststellen. Der Graph zeigt jedoch, dass zu einem bestimmten Zeitpunkt vor dem beobachteten Jahr unendlich viele infizierte Personen in Deutschland leben, was offensichtlich nicht möglich ist.

Bearbeite den Lückentext