Digitale Werkzeuge in der Schule/Basiswissen Analysis/Optimierungsprobleme

Info

In diesem Kapitel kannst du etwas zum Thema Optimierungsprobleme lernen.

In Aufgaben, die orange gefärbt sind, kannst du Gelerntes wiederholen und vertiefen.

Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit.

Und Aufgaben mit grüner Hinterlegung sind Knobelaufgaben.

Aufgaben, die mit einem ⭐ gekennzeichnet sind, sind nur für den LK gedacht.

In diesem Kapitel erklären wir dir zunächst, was Optimierungsprobleme sind. Dabei werden wir wichtige Begriffe wiederholen.

Anschließend kannst du selbstständig Aufgaben bearbeiten.

Viel Erfolg!

Einführung: Optimierungsprobleme

Was sind Optimierungsprobleme?

Optimierungsprobleme , oder auch Extremwertprobleme, beschreiben eine Aufgabenform, bei der nach dem optimalen Wert einer Funktion gefragt wird. Dieser optimale Wert ist oftmals ein Extremwert, also ein Maximum oder ein Minimum.

Die Berechnung erfolgt dabei im Sachzusammenhang, es wird also beispielsweise nach dem minimalen Volumen einer Schachtel gefragt, die man mit einem Blatt Papier falten kann, oder nach dem maximalen Flächeninhalt eines Grundstücks, das man mit einer bestimmten Meterzahl an Zaunteilen einzäunen kann.

Die Funktion, deren Extremwert es zu bestimmen gilt, muss also noch ermittelt werden.

Vorgehen beim Lösen von Optimierungsproblemen

So löst du Optimierungsprobleme

Bei Optimierungsproblemen geht es stets darum, dass eine bestimmte Größe optimiert werden soll. So wird z. B. eine optimale Verpackung für Reis oder die optimale Anzahl an Zahnpasten gesucht, die in einen Karton passen - es geht also um eine Anwendungssituation. Das Ergebnis eines Optimierungsproblems ist daher auch meist kein exakter Wert sondern ein Näherungswert. Dieser muss natürlich sinnvoll gewählt sein.

Zur Lösung eines Optimierungsproblems muss man zunächst die Aufgabe genau lesen und verstehen. Hierbei kann man sich die folgenden Fragen stellen: Worum geht es? Welche Größen kommen vor und wie hängen sie zusammen? Welche Größe soll nun optimiert, also maximiert oder minimiert werden?

Der optimale Wert bedeutet mathematisch, den Extremwert einer Funktion zu bestimmen. Du musst also das Optimierungsproblem als Funktion ausdrücken und dabei die anderen Größen miteinbeziehen. Mit dieser Funktion kannst du dann den optimalen Wert bestimmen.

Aufgabe 1: Beispiel

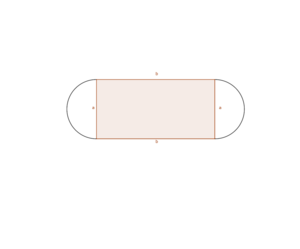
Ein Sportplatz mit einer 400-m-Laufbahn soll so angelegt werden, dass das Fußballfeld möglichst groß ist. Die seitlichen Kurven des Sportplatzes sollen Halbkreise sein.

a) Für welche Länge und für weiche Breite wird das Fußballfeld im Inneren des Sportplatzes maximal?

b) Wie groß ist das Fußballfeld?

Rechenweg

Gegeben ist die Länge der Laufbahn um den Sportplatz herum, also der Umfang des Sportplatzes. Maximiert werden soll die Größe des Fussballfeldes, also der rechteckige Flächeninhalt $A$ innerhalb des Sportplatzes.

Die Formel zum Flächeninhalt ist $A=2=a \cdot b$. Über die Größen selbst weißt du ebenfalls etwas durch den Umfang: $U=2 \cdot a+\pi\cdot b$. Stelle die Formel für den Umfang nun nach $a$ um und erhalte: $a=\frac{400-\pi \cdot b}{2}$

Setze nun deine Formel für $a$ in den Flächeninhalt ein. So erhälst du die folgende Zielfunktion:

$A(b)=\frac{400-\pi \cdot b}{2} \cdot b=\frac{-\pi \cdot b^2}{2}+200 \cdot b$ Für diese Funktion kann $b$ nur zwischen $0$ und $200$ liegen, also $0<b<200$

Nun musst du den optimalen Wert berechnen. Gesucht ist hier das Maximum. Bilde dazu die Ableitungen:

1. $A'(b)= -\pi \cdot b + 200 \cdot b$
2. $A''(b) = - \pi$

Mit der notwendigen Bedingung $A'(b)=0$ erhälst du dann $b=\frac{200}{pi} = 63,66$. Mit der hinreichenden Bedingung folgt $A''(b)=-\pi \neq 0$, somit erfüllt $b$ alle Bedingungen.

Berechne nun $a$ und den Flächeninhalt:

1. $a=\frac{400-\pi \cdot \frac{200}{pi}}{2} = 100$ und
2. $A = 100 \cdot 63,66 = 6366 m$

Lösung

a) Der Flächeninhalt des Fussballfeldes wird für eine Breite von $63,66m$ und eine Höhe von $100m$ maximal.

b) Der Flächeninhalt wird auf $6366 m$ maximiert.

Aufgabe 2: Das optimale Paket

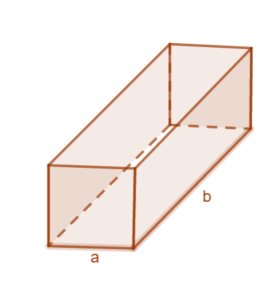
Eine Kartonfabrik stellt quaderförmige Pakete mit quadratischen Seitenflächen ($a$) her. Damit die Pakete nicht zu unhandlich werden, sollen noch zwei Bedingungen erfüllt sein:

• Die Länge ($b$) soll nicht größer als $200cm$ sein.
• Länge ($b$) plus Umfang einer quadratischen Seitenfläche soll $360cm$ groß sein.
  

a) Ermittle die Abmessungen des Pakets mit dem größten Volumen.

b) Gebe das maximale Volumen an.

Tipp zum Aufstellen der Zielfunktion

Rechne Höhe ($a$) $*$ Breite ($a$) $*$ Länge ($b$), um das Volumen eines Quaders (Paketes) zu ermitteln.

Tipp für eine geeignete Nebenbedingung

Nutze die zweite Bedingung, stelle eine Gleichung auf und stelle diese nach $b$ um.

Zweite Bedingung: Länge ($b$) plus Umfang einer quadratischen Seitenfläche soll $360cm$ groß sein. Den Umfang einer quadratischen Seitenfläche erhältst du, indem du $4*a$ rechnest.

Tipp zur Bestimmung der Definitionsmenge

Die Definitionsmenge für die Zielfunktion $V(a)$ ergibt sich aus der Bedingung für die Länge ($b$). Die Länge muss zum einen größer gleich $0$ und zum anderen kleiner gleich $200$ sein. Also gelten die folgenden zwei Ungleichungen, die du einfach nach a auflösen kannst. $0$$\leq$$360-4*a$ und

$200$$\geq$$360-4*a$.

Lösung der Aufgabe

Zielfunktion aufstellen: Um das Volumen des Paktes zu errechnen, verwenden wir die folgende Funktion, die von den Variablen $a$ und $b$ abgängig ist: $V(a,b) = a * a * b = a^2 *b$.

Nebenbedingung aufstellen: Durch die zweite Bedingung können wir die folgende Gleichung aufstellen. $b + 4*a = 360$. Die Gleichung stellen wir nach $b$ um und erhalten: $b = 360 - 4*a$. Nun können wir $b$ in die Zielfunktion $V(a,b)$ einsetzen, welche dann durch noch von der Variable $a$ abhängt. Wir schreiben dann für die Funktion $V(a)$ und erhalten $V(a) = -4*a^3 + 360 a^2$.

Definitionsmenge angeben: Wir wollen nun eine Definitionsmenge für die Funktion $V(a)$ angeben. Diese erhalten wir, indem wir uns die Bedingung für die Länge ($b$) anschauen. Offensichtlich muss die Länge größer gleich $0$ sein. Es gilt also: $360 - 4*a \geq 0$. Durch das Umstellen nach $a$ folgt:$a \leq 90$. Außerdem muss die Länger kleiner gleich $200 cm$ sein. Es gilt also: <$360 - 4*a \leq 200$. Durch das Umstellen nach $a$ folgt: $a \geq 40$. Insgesamt ergibt das also $40 \leq a \leq 90$.

Nun sollen die Extremstellen von $V(a)$bestimmt werden.

$V'(a) = -12a^2 + 720a$

$V''(a) = -24a + 720$.

Notw. Bedingung: $V'(a) = 0$.

$-12a^2 + 720a = 0$ (Klammere das $a$ aus und wende den Satz vom Nullprodukt an. Alternativ kannst du auch die pq-Formel anwenden) $(-12a + 720)a = 0$

$-> a=0$ oder $-12a + 720 = 0$. Da $a \geq 40$ muss $-12a + 720 = 0$ gelten, also $a = 60$.

Durch das Einsetzen von $a = 60$ in $V''(a)$ folgt, dass $V(a)$ an dieser Stelle einen Hochpunkt besitzt.

Breite und Höhe sind also $60 cm$. Die Länge ergibt sich durch das einsetzen von $a = 60$ in $b = 360 - 4*a$. $b = 120 cm$.

Das Volumen bestimmen: Wir berechnen nun das Volumen des optimalen Paketes, indem wir $60 * 60 * 120$ berechnen.

Das maximale Volumen beträgt also $432 000 cm^3$.

Aufgabe 3: Die optimale Pommestüte

Leon möchte aus einem kreisförmigen Stück Papier mit dem Radius $s=10cm$ eine Pommestüte formen.

Dazu schneidet er den Kreis längs eines Radius ein. Nun versucht Leon die Pommestüte so zu formen, sodass das Volumen der Pommestüte maximal ist, damit auch möglichst viele Pommes hineinpassen.

Was ist das maximale Volumen der Pommestüte?

Tipp zur Erfassung des Problems

Beachte, dass der Radius des Stücks Papier $s=10cm$ der Mantellinie $s$ des Kegels entspricht.

Tipp zur Bestimmung des Volumens

Das Volumen der Pommestüte errechnet man mit der Formel $V(r,h)=\frac{1}{3}\pi*r^2*h$.

Tipp für eine geeignete Nebenbedingung

Mit Hilfe vom Satz des Pythagoras kannst du $s^2$ bestimmen. Durch geeignetes Umstellen nach $r^2$ erhältst du schließlich eine geeignete Nebenbedingung.

Lösung

Leon möchte aus einem kreisförmigen Stück Papier eine Pommestüte formen, in der möglichst viele Pommes hineinpassen. Zu optimieren ist also das Volumen $V(r,h)=\frac{1}{3} \cdot\pi\cdot r^2 h$ der Pommestüte.

Rollt Leon das Stück Papier nicht, so ist ist das Volumen $V = 0$. Rollte Leon das Stück Papier ganz zusammen, so ist $s = h = 10$.

Gegeben ist die Mantellinie mit $s=10$ der Pommestüte. Außerdem ist das Volumen der Pommestüte von den Variablen $r$(Radius) und $h$(Höhe) abhängig. Mit dem Satz des Pythagoras ergibt sich $r^2 + h^2 = 10^2$. Stelle diese Gleichung nun nach $r$ um und erhalte $r^2 = 100 - h^2$.

Setze diesen Ausdruck nun für $r^2$ in die Formel für das Volumen ein. Du erhälst folgende Zielfunktion: $V(h)= \frac{1}{3} \pi (100-h^2)h = -\frac{1}{3} \pi h^3 + \frac{100}{3} \pi h$.

Für diese Funktion kann $h$ nur zwischen $0$ und $10$ liegen, also $0<h<10$.

Da es sich um eine Anwendungssituation handelt, reicht ein guter Näherungswert.

Die Ableitungsfunktion lautet $V'(h)=- \pi*h^2 + \frac{100}{3} * \pi$.

Das maximale Volumen der Pommestüte beträgt ca. $403cm^3$

Globales Extremum und Randextremum

Merke

Der größte Funktionswert unter allen Funktionswerten in der Definitionsmenge heißt globales Maximum. Der kleinste Funktionswert unter allen Funktionswerten in der Definitionsmenge heißt globales Minimum.

Ein globales Extremum an einer Randstelle der Definitionsmenge heißt Randextremum.

Übung

Aufgabe 4

Gegeben ist der Graph einer Funktion $f$ mit $f(x)=(x-3)^2+2,5$ im Intervall $[0,3]$. Ein achsenparalleles Rechteck wird so gelegt, dass ein Eckpunkt der Koordinatenursprung ist und der gegenüberliegende Eckpunkt auf dem Graphen von f liegt.

Welches der möglichen Rechtecke hat den größten Flächeninhalt?

Lösung

Mit $x,y$ in $cm$ berechnen wir den Flächeninhalt mit der Funktion $A(x,y)=x*y$.

Die Nebenbedingung ist die angegebene Funktion $f(x)=f(x)=(x-3)^2+2,5$.

Setzt man nun die Nebenbedingung in die Funktion $A(x,y)$ ein, so erhalten wir $A(x)=x^3-6x^2+11x$. Die Funktion heißt nun $A(x)$, da sie nur noch von der Unbekannte $x$ abhängt.

Nun lässt sich mit Hilfe der notwendigen Bedingung $A'(x)=0$ und der hinreichenden Bedingung für Hochpunkte $A''(x) < 0$ die Stelle des lokalen Hochpunktes bestimmen. Anschließend setzen wir $x$ in die Ausgangsfunktion $A(x)$ ein und erhalten nun den lokalen Hochpunkt $HP(1,59|7,14)$.

Zuletzt prüfen wir noch die Randpunkte.

$A(0)=0$ und $A(3)=7,5$.

Damit liegt der globale Hochpunkt an der Stelle $x=3$.

Der Flächeninhalt ist also am größten, wenn der zweite Eckpunkt des achsenparallelen Rechteckes an die Stelle $x=3$ gelegt wird. Der Flächeninhalt beträgt dann $7,5cm^2$

Optimierungsprobleme & Funktionenscharen

Berechnung von Extremwerten im Fall einer Funktionenschar

In bestimmten Fällen kann es vorkommen, dass die erhaltene Funktion nicht nur von einer Variable $x$ abhängt, sondern außerdem von einem Parameter $a$.

In diesem Fall ändert sich die Vorgehensweise bei der Berechnung des Extremwertes zwar nicht, allerdings ist das erhaltene Ergebnis dann abhängig von a.

Aufgabe 5 ⭐

Gegeben ist die Funktionenschar $f_t(x)=x^2-4x-t^2-2t$.

Für welchen Wert von $t$ liegt der Tiefpunkt der Funktionenschar am höchsten?

Tipp 1

Die zu optimierende Größe ist der Funktionswert am Tiefpunkt der Funktion.

Berechne also zunächst den Tiefpunkt der Funktion in Abhängigkeit von $t$.

Lösung

Ableiten der Funktion ergibt:

$f'(x)=2x-4$ $f''(x)= 2$

Für ein Minimum muss gelten: $f'(x)=0$ und $f''(x)>0$.

$f'(x)=0$

$<=> 2x-4=0$

$<=> 2x=4$

$<=> x=2$

$f''(2) = 2 > 0 =>$ Minimum

Setze nun $x=2$ in $f(x)$ ein, um den Funktionswert am Minimum zu bestimmen:

$f(2)=2^2-4*2-t^2-2t$

$<=> f(2)=4-8-t^2-2t$

$<=> f(2)=-4-t^2-2t$

Bezeichnen wir den Funktionswert am Tiefpunkt mit einer neuen Gleichung $g$, so ergibt sich also:

$g(t)=-4-t^2-2t$.

Tipp 2

Gesucht ist das $t$, für das der Funktionswert maximal ist, also das Maximum der Funktion $g(t)$.

Tipp 3

Prüfe die hinreichende Bedingung: $g'(t)=0$ und $g''(t)<0$.

Gesamtlösung

Die zu optimierende Größe ist der Funktionswert am Tiefpunkt der Funktion.

Berechne also zunächst den Tiefpunkt der Funktion in Abhängigkeit von $t$:

Ableiten der Funktion ergibt:

$f'(x)=2x-4$ $f''(x)= 2$

Für ein Minimum muss gelten: $f'(x)=0$ und $f''(x)>0$.

$f'(x)=0$

$<=> 2x-4=0$

$<=> 2x=4$

$<=> x=2$

$f''(2) = 2 > 0 =>$ Minimum

Setze nun $x=2$ in $f(x)$ ein, um den Funktionswert am Minimum zu bestimmen:

$f(2)=2^2-4*2-t^2-2t$

$<=> f(2)=4-8-t^2-2t$

$<=> f(2)=-4-t^2-2t$

Bezeichnen wir den Funktionswert am Tiefpunkt mit einer neuen Gleichung $g$, so ergibt sich also:

$g(t)=-4-t^2-2t$.

Gesucht ist das $t$, für das der Funktionswert maximal ist, also das Maximum der Funktion $g(t)$.

Bilde zunächst wieder die Ableitungen $g'(t)$ und $g''(t)$:

$g'(t)=-2t-2$

$g''(t)=-2$

Bei einem Maximum muss gelten: $g'(t)=0$ und $g''(t)<0$.

$g'(t)=0$

$<=>-2t-2=0$

$<=>-2t=2$

$<=>t=-1$

$g''(-1)=-2<0 =>$ Maximum

Der Funktionswert des Tiefpunktes ist also für $t=-1$ maximal.