Digitale Werkzeuge in der Schule/Basiswissen Analysis/Steckbriefaufgaben: Unterschied zwischen den Versionen
Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 49: | Zeile 49: | ||
|1= | |1= Den Schnittpunkt einer Funktion mit der y-Achse nennt man '''<math>y</math>-Achsenabschnitt'''. Ist <math>y_s</math> der <math>y</math>-Achsenabschnitt einer Funktion <math>f</math>, liegt der Punkt <math>P_y(0|y_s)</math>, dessen x-Wert gleich <math>0</math> ist, auf dem Funktionsgraphen von <math>f</math>. | ||
Den <math>y</math>-Achsenabschnitt errechnest Du, indem Du in den Funktionsterm für <math>x</math> 0 einsetzt: <math>f(0)=y_s</math>. | |||
| Zeile 66: | Zeile 66: | ||
|3= Beispiel verbergen}} | |3= Beispiel verbergen}} | ||
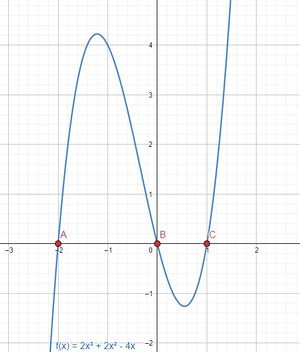
Der <math>y</math>-Achsenabschnitt ist immer gleich dem letzten Koeffizienten der Funktion, welcher nicht mit <math>x</math> multipliziert wird. Sie lässt sich also immer aus der Funktionsgleichung ablesen. | |||
|2= Schnittpunkte mit der y-Achse | |2= Schnittpunkte mit der y-Achse | ||
| Zeile 154: | Zeile 154: | ||
|3= Beispiel}} | |3= Beispiel}} | ||
{{Box|1= Extrema und | {{Box|1= Extrema und Wendepunkte | ||
|2= {{Lösung versteckt | |2= {{Lösung versteckt | ||
|1= Mit einem '''Extremwert''' bezeichnet man ein lokales oder globales Maximum (Hochpunkt) oder Minimum (Tiefpunkt). Nimmt der Funktionswert <math>f(x)</math> an einer Stelle <math>x</math> den größten bzw. kleinsten Wert innerhalb eines Intervalles um <math>x</math> an, so spricht man von einem lokalen Maximum bzw. lokalem Minimum. Ist der Funktionswert bei <math>x</math> der größte bzw. kleinste Wert für den gesamten Definitionsbereich der Funktion, so nennt man ihn globales Maximum bzw. globales Minimum. | |1= Mit einem '''Extremwert''' bezeichnet man ein lokales oder globales Maximum (Hochpunkt) oder Minimum (Tiefpunkt). Nimmt der Funktionswert <math>f(x)</math> an einer Stelle <math>x</math> den größten bzw. kleinsten Wert innerhalb eines Intervalles um <math>x</math> an, so spricht man von einem lokalen Maximum bzw. lokalem Minimum. Ist der Funktionswert bei <math>x</math> der größte bzw. kleinste Wert für den gesamten Definitionsbereich der Funktion, so nennt man ihn globales Maximum bzw. globales Minimum. | ||
Version vom 3. Mai 2020, 15:06 Uhr
Allgemeine Hinweise
Eigenschaften von ganzrationalen Funktionen
In diesem Abschnitt werden wir kurz die Eigenschaften von ganzrationalen Funktionen wiederholen. Solltest du das Kapitel Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung noch nicht bearbeitet haben, empfehlen wir dir, dich zuerst damit vertraut zu machen. Wenn du dich fit fühlst beim Thema Funktionseigenschaften, kannst du die Wiederholung überspringen und dein Wissen im Quiz im unteren Bereich dieses Abschnitts testen.
Quiz
Einführung
Auf dieser Seite lernst Du, wie Du Gleichungssysteme mit mehr als einer Variablen lösen kannst. Falls Du dir noch unsicher bist, wie man eine Gleichung mit nur einer Variable löst, versuche folgendes Beispiel zu lösen. Falls Du das aber noch kannst, dann überspringe das Beispiel gerne.
Das Einsetzungsverfahren
Aufgaben zum Einsetzungsverfahren
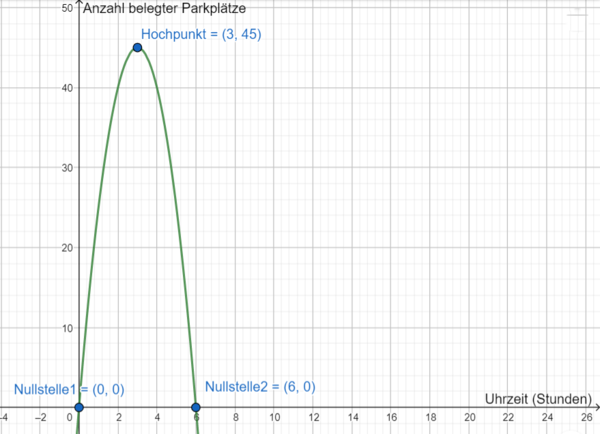
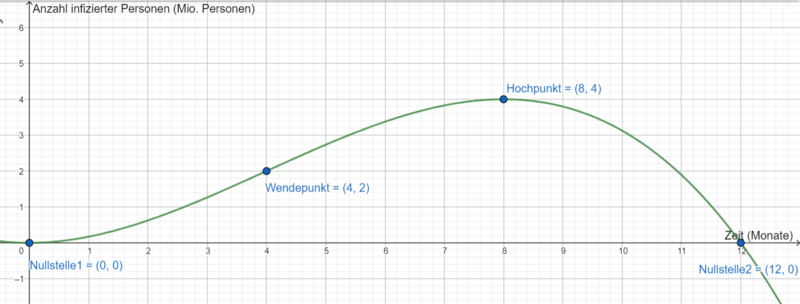
Quadratische Funktionen im Sachzusammenhang
Das Gauß-Verfahren
Aufgaben zum Gauß-Verfahren
Kubische Funktionen im Sachzusammenhang