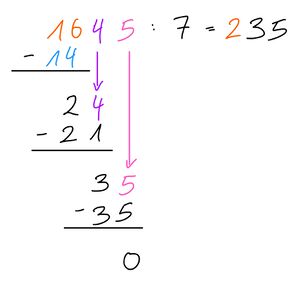|
|
| Zeile 351: |
Zeile 351: |
|
| |
|
| 1) Wir rechnen von hinten nach vorne | | 1) Wir rechnen von hinten nach vorne |
| | |
| 2) Beginne mit der rechten Ziffer der hinteren Zahl (der Einerstelle) und multipliziere sie mit jeder Ziffer der vorderen Zahl | | 2) Beginne mit der rechten Ziffer der hinteren Zahl (der Einerstelle) und multipliziere sie mit jeder Ziffer der vorderen Zahl |
| [[Datei:Schriftliches Multiplizieren.jpg|mini]] | | [[Datei:Schriftliches Multiplizieren.jpg|mini]]|Arbeitsmethode |
| |Arbeitsmethode | | | Farbe = {{Farbe|grün|dunkel}} |
| |Farbe = {{Farbe|grün|dunkel}} | |
| }} | | }} |
|
| |
|
Version vom 14. Mai 2024, 11:29 Uhr
Info
Zahlen begegnen dir jeden Tag: Mitglieder einer AG, Besucher im Stadion, verkaufte Handys. Das sind „natürliche“ Zahlen. Wenn du loszählst, 0, 1, 2, 3 und so weiter, erhältst du die natürlichen Zahlen.
In diesem Lernpfadkapitel widmen wir uns den natürlichen Zahlen.
In diesem Kapitel wiederholst du, ...
- ... schriftliches addieren und subtrahieren natürlicher Zahlen
- ... Fachbegriffe und Rechengesetze für die Addition und Subtraktion
- ... schriftliches multiplizieren und dividieren natürlicher Zahlen
- ... Fachbegriffe und Rechengesetze für die Multiplikation und Division
Bei den Aufgaben unterscheiden wir folgende Typen:
- In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
- Aufgaben in pinker Farbe sind Aufgaben mittlerer Schwierigkeit.
- Und Aufgaben mit lilanem Streifen sind Knobelaufgaben.
Viel Erfolg!
Schriftliches Addieren und Subtrahieren von natürlichen Zahlen
(*) Aufgabe 1: Zahlenmauer
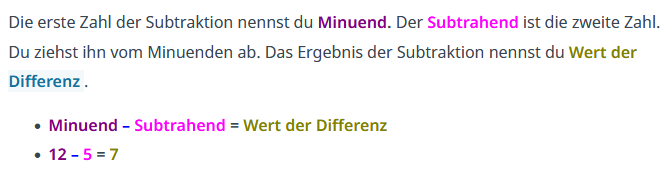
Fachbegriffe und Rechengesetze
(**) Aufgabe 2: Fachbegriffe zur Addition und Subtraktion
Merksatz zu Fachbegriffen
(**) Aufgabe 3: Die Rechengesetze
Merksatz Vertauschungsgesetz (Kommutativgesetz)
Das Vertauschungsgesetz (Kommutativgesetz) besagt: Beim Addieren kannst du die Summanden vertauschen. Das Ergebnis bleibt gleich. Beispiel: 83 + 92 =92 + 83
Vorsicht bei der Subtraktion
Untersuche das Vertauschen bei der Subtraktion.
Beispiel:
100 - 50 + 45 = 95
100 - 45 + 50 = 105
Also ist 100 - 50 + 45 nicht das gleiche wie 100 - 45 + 50.
Beim
Subtrahieren kannst du
Minuend und
Subtrahend nicht vertauschen. Das Vertauschen von Subtrahend und Minuend führt nicht zum richtigen Ergebniss.
Merksatz Verbindungsgesetz (Assoziativgesetz)
Das Verbindungsgesetz (Assoziativgesetz) besagt: Beim Addieren kannst du beliebig Klammern setzen oder weglassen. Das Ergebnis bleibt gleich. (Hinweis: Du rechnest zuerst die Klammer wegen Klammer vor Punkt vor Strich aus).
Beispiel:
26 + 73 + 37 = (26 + 73) + 37
26 + 73 + 37 = 26 + (73 + 37)
Vorsicht bei der Subtraktion
Untersuche das Setzen von Klammern bei der Subtraktion.
Beispiel:
(123 - 73) - 27 = 50 - 27 = 23
123 - (73 - 27) = 123 - 46 = 77
Also ist (123 - 73) - 27 nicht das gleiche wie 123 - (73 - 27).
Beim
Subtrahieren kannst du
nicht beliebig Klammern setzen. Das Setzen von Klammern bei der Subtraktion führt zu unterschiedlichen Ergebnisse.
Addition von natürlichen Zahlen
(*) Aufgabe 4: Schriftliches Addieren mit großen Zahlen
Merksatz zur schriftlichen Addition
Die schriftliche Addition hilft dir, größere und mehrere Zahlen zu addieren.
Schreibe die Zahlen immer stellengerecht untereinander:
Einer unter Einer, Zehner unter Zehner, ...
Es gibt zwei verschiedene Arten der schriftlichen Addition:
- Die Addition ohne Übertrag
- Die Addition mit Übertrag
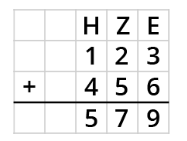
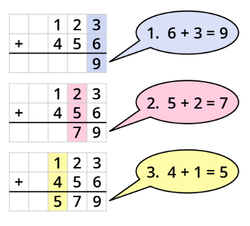
Die Addition ohne Übertrag
Du beginnst mit der Addition rechts.
Beispiel:
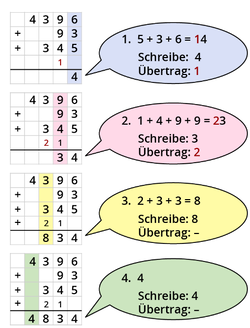
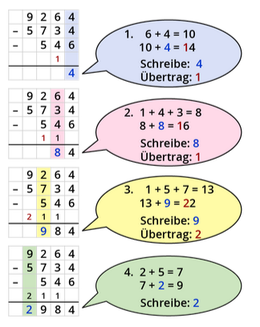
Die Addition mit Übertrag
Du beginnst wieder rechts mit der Addition.
Beispiel:
Subtraktion von natürlichen Zahlen
(*) Aufgabe 5: Schriftliches Subtrahieren
(**) Aufgabe 6: Schriftliches Subtrahieren mit großen Zahlen
Merksatz zur schriftlichen Subtraktion
Die schriftliche Subtraktion hilft dir, größere und mehrere Zahlen zu subtrahieren.
Schreibe die Zahlen immer stellengerecht untereinander:
Einer unter Einer, Zehner unter Zehner, ...
Es gibt zwei verschiedene Arten der schriftlichen Subtraktion:
- Die Subtraktion ohne Übertrag
- Die Subtraktion mit Übertrag
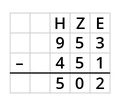
Die Subtraktion ohne Übertrag
Du beginnst mit der Subtraktion rechts. Die untere Zahl wird dabei zur oberen Zahl ergänzt.
Beispiel:
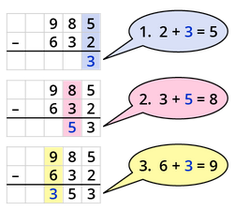
Die Subtraktion mit Übertrag
Du beginnst wieder rechts mit der Subtraktion.
Beispiel:
Gemischte Aufgaben (Addition, Subtraktion, Fachbegriffe)
Hinweis: Verfahren bei Textaufgaben
Suche bei Anwendungsaufgaben nach Signalwörtern. Übersetze den Text in eine Rechnung, rechne aus und schreibe einen Antwortsatz in dein Heft.
Diese Signalwörter sagen dir, dass du subtrahierst:
- vermindert
- weniger
- Abnahme
- wegnehmen
- verringern
- abziehen
Diese Signalwörter sagen dir, dass du addierst:
- vermehrt
- mehr
- Zuwachs
- dazu
- hinzufügen
(**) Aufgabe 7: Waffelverkauf
Die 6b hat 120 € in der Klassenkasse. Mit einem Waffelverkauf hat die 6b 48 € verdient. Für ihr Sommerfest gibt die Klasse 80 € für Getränke und Essen aus. Wie viel Geld hat die 6b nach dem Sommerfest in der Klassenkasse?
Rechnung: 120 + 48 - 80 = 168 - 80 = 88
Die 6b hat nach dem Sommerfest 88 € in der Klassenklasse.
Aysen trainiert und läuft dreimal in der Woche. Am Montag läuft sie 2 km, am Mittwoch 3 km, aber am Freitag nur 800 m. Wie viel ist sie am Ende der Woche gelaufen?
Wenn in einer Aufgabe Zahlen mit verschiedenen Einheiten vorkommen, wandelst du die Einheiten so um, dass du nur noch eine Einheit hast. Dann kannst du wie gewohnt rechnen.
(***) Aufgabe 9: Knobelaufgabe
Schriftliches Multiplizieren und Dividieren von natürlichen Zahlen
(*) Aufgabe 1: Multiplikation Pferderennen
(*) Aufgabe 2: Division Zuordnen
Fachbegriffe und Rechengesetze
Merksatz zu den Fachbegriffen der Multiplikation und Division
Multiplizieren oder "mal rechnen" bedeutet, dass du eine Zahl immer wieder dazu nimmst. Zum Beispiel, wenn du 3•4 rechnest, bedeutet das, dass du die Zahl 3 vier Mal nimmst und zusammenzählst. Also: 3 + 3 + 3+ 3 = 12. Das ist das Ergebnis von 3•4. Das Produkt ist das Ergebnis einer Multiplikation und das Vielfache ist das Ergebnis der Multiplikation einer Zahl mit einer anderen ganzen Zahl.
Division oder "geteilt durch rechnen" bedeutet, dass du etwas in gleich große Teile aufteilst. Stell dir vor, du hast 12 Gummibärchen und möchtest sie auf 3 Freunde aufteilen. Du würdest 12 durch 3 teilen, um herauszufinden, wie viele Gummibärchen jeder Freund bekommt. In diesem Fall würden alle 3 Freunde Gummibärchen bekommen, weil 12 ÷ 3 = 4. Das ist die Division! Es hilft uns, Dinge fair aufzuteilen. Der Divisor ist die Zahl, durch die du teilst und der Quotient ist das Ergebnis, wenn du Zahlen miteinander teilst. Achtung: Du darfst nicht durch Null teilen!
(*) Aufgabe 3: Fachbegriffe zur Multiplikation und Division
(**) Aufgabe 4: Fachbegriffe zur Multiplikation und Division
Merksatz Vertauschungsgesetz (Kommutativgesetz)
Das Vertauschungsgesetz (Kommutativgesetz) besagt: Beim Multiplizieren kannst du die Faktoren vertauschen. Das Ergebnis bleibt gleich. Beispiel: 
Vorsicht bei der Division
Untersuche das Vertauschen bei der Division.
Beispiel:

Also ist  nicht das gleiche wie
nicht das gleiche wie  .
.
Beim
Dividieren kannst du
Dividend und
Divisor nicht vertauschen. Das Vertauschen von Dividend und Divisor führt nicht zum richtigen Ergebniss.
Merksatz Verbindungsgesetz (Assoziativgesetz)
Das Verbindungsgesetz (Assoziativgesetz) besagt: Beim Multiplizieren kannst du beliebig Klammern setzen oder weglassen. Das Ergebnis bleibt gleich. (Hinweis: Du rechnest zuerst die Klammer wegen Klammer vor Punkt vor Strich aus).
Beispiel:



Vorsicht bei der Division
Untersuche das Setzen von Klammern bei der Division.
Beispiel:


Also ist  nicht das gleiche wie
nicht das gleiche wie  .
.
Beim
Dividieren kannst du
nicht beliebig Klammern setzen. Das Setzen von Klammern bei der Division führt zu unterschiedlichen Ergebnisse.
Multiplikation von natürlichen Zahlen
Merksatz schriftliches Multiplizieren
Für schriftliches Multiplizieren werden wir unsere Faktoren in Einer, Zehner und Hunderter (ggf. auch Tausender und höher, falls die Aufgabe dies verlangt) zerlegen. Die schriftliche Multiplikation basiert dann darauf, die einzelnen Ziffern zu multiplizieren und die Ergebnisse schließlich zu addieren.
Wichtig:
1) Wir rechnen von hinten nach vorne
2) Beginne mit der rechten Ziffer der hinteren Zahl (der Einerstelle) und multipliziere sie mit jeder Ziffer der vorderen Zahl
(*) Aufgabe 5: Schriftliches Multiplizieren mit Zahlen bis Tausend
Multipliziere schriftlich mithilfe der App. Wenn kein Übertrag vorhanden ist, trage eine 0 an dieser Stelle ein.
(***) Aufgabe 6: Schriftliches Multiplizieren mit großen Zahlen
Multipliziere schriftlich mithilfe der App.
Division von natürlichen Zahlen
Merksatz schriftliches Dividieren
Vorgehen:
1)Du teilst die Ziffer der linken Zahl durch die rechte Zahl (Divisor ) und schreibst das Ergebnis hinter das Gleichheitszeichen.
2) Du multiplizierst das Teilergebnis mit dem Divisor und schreibst es mit Minus unter linke Zahl.
3) Du subtrahierst (Minus-Rechnen)
4) Du holst die weiteren Ziffern "herunter" und wiederholst die Schritte
(*) Aufgabe 7: Schriftliches Dividieren mit Zahlen bis Tausend
Dividiere schriftlich mithilfe der App.
(**) Aufgabe 8: Schriftliches Dividieren mit großen Zahlen
Dividiere schriftlich mithilfe der App.
Gemischte Aufgaben (Multiplikation, Division, Fachbegriffe)
Hinweis: Verfahren bei Textaufgaben
Suche bei Anwendungsaufgaben nach Signalwörtern. Übersetze den Text in eine Rechnung, rechne aus und schreibe einen Antwortsatz in dein Heft.
Diese Signalwörter sagen dir, dass du multiplizierst:
- ...mal so viel
- das ...-fache
- multiplizieren
- verdoppeln
- vervielfachen
- je
Diese Signalwörter sagen dir, dass du dividierst:
- aufteilen
- halbieren
- austeilen
- durch
- dividieren
(**) Aufgabe 9: Erkennen von Signalwörtern der Multiplikation und Division
(**) Aufgabe 10: Ein Ausflug zum Möhnesee
Tom, Karl, Tina, Cleo, Max, Sophia und Sarah wollen sich für einen Ausflug zum Möhnesee im Sauerland ein Schlauchboot kaufen. Für das Schlauchboot müssen sie zusammen 371€ bezahlen. Den Preis möchten die Freunde untereinander aufteilen. Wie viel muss jede bzw. jeder zahlen?
Rechnung: 
Jede bzw. jeder muss 53€ bezahlen.
(**) Aufgabe 11: Schulkinder
Eine Schuldirektorin erzählt euch über die Veränderungen der Anzahl der Schulkinder in ihrer Schule.
Sie berichtet, dass zur Zeit insgesamt 412 Schulkinder die erste und zweite Klasse besuchen. Das sind nur halb so viele Schulkinder wie vor 6 Jahren. Die dritte und vierte Klasse besuchen derzeit 378 Schulkinder. Das sind dreimal so viele Schulkinder wie vor 6 Jahren.
Wie viele Schulkinder besuchten vor 6 Jahren die erste und zweite Klasse und die dritte und vierte Klasse?
Das Gegenteil von der "Hälfte" ist das "Doppelte".
Rechnung:


Vor 6 Jahren besuchten die erste und zweite Klasse insgesamt 824 Schulkinder und die dritte und vierte Klasse insgesamt 126 Schulkinder.
(***) Aufgabe 12: Wer wird Multiplikations- und Divisionsmeister?