Digitale Werkzeuge in der Schule/Kleine Lernstandserhebung zur Doppeljahrgangsstufe 5/6/Natürliche Zahlen/Natürliche Zahlen schriftlich addieren und subtrahieren: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Kleine Lernstandserhebung zur Doppeljahrgangsstufe 5/6 | Natürliche Zahlen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 146: | Zeile 146: | ||
{{Box | {{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz Vertauschungsgesetz (Kommutativgesetz)|Das '''Vertauschungsgesetz (Kommutativgesetz)''' besagt: Beim Addieren kannst du die Summanden vertauschen. Das Ergebnis bleibt gleich. '''Beispiel'''<nowiki>: 83 + 92 =92 + 83</nowiki> | ||
| | |||
'''''Vorsicht bei der Subtraktion''''' | |||
Untersuche das Vertauschen bei der Subtraktion. | |||
'''Beispiel''': | |||
<nowiki>100 - 50 + 45 = 95 </nowiki> | |||
<nowiki>100 - 45 + 50 = 105 </nowiki> | |||
''' | Also ist 100 - 50 + 45 '''nicht '''das gleiche wie 100 - 45 + 50. | ||
Beim '''''Subtrahieren '''''kannst du '''Minuend''' und '''Subtrahend''' '''nicht''' vertauschen. Das Vertauschen von Subtrahend und Minuend führt nicht zum richtigen Ergebniss.|Hervorhebung2 | |||
}}{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz Verbindungsgesetz (Assoziativgesetz)|Das '''Verbindungsgesetz (Assoziativgesetz)''' besagt: Beim Addieren kannst du beliebig Klammern setzen oder weglassen. Das Ergebnis bleibt gleich. (Hinweis: Du rechnest zuerst die Klammer wegen Klammer vor Punkt vor Strich aus). | |||
'''Beispiel''': | |||
<nowiki>26 + 73 + 37 = (26 + 73) + 37 </nowiki> | |||
<nowiki>26 + 73 + 37 = 26 + (73 + 37)</nowiki> | |||
''' | '''''Vorsicht bei der Subtraktion''''' | ||
Untersuche das Setzen von Klammern bei der Subtraktion. | |||
'''Beispiel''': | |||
<nowiki>(123 - 73) - 27 = 50 - 27 = 23 </nowiki> | |||
<nowiki>123 - (73 - 27) = 123 - 46 = 77 </nowiki> | |||
Also ist (123 - 73) - 27 '''nicht '''das gleiche wie 123 - (73 - 27). | |||
''' | Beim '''''Subtrahieren '''''kannst du '''nicht '''beliebig Klammern setzen. Das Setzen von Klammern bei der Subtraktion führt zu unterschiedlichen Ergebnisse.|Hervorhebung2 | ||
}} | |||
Version vom 16. April 2024, 09:21 Uhr
Info
In diesem Lernpfadunterkapitel wiederholst du...
- natürliche Zahlen schriftlich zu addieren und subtrahieren
- Fachbegriffe, Rechengesetze sowie Rechenvorteile zur Addition und Subtraktion
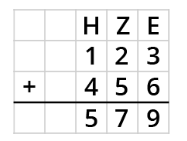
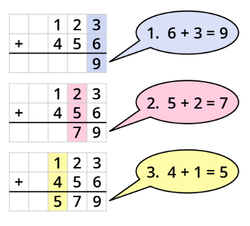
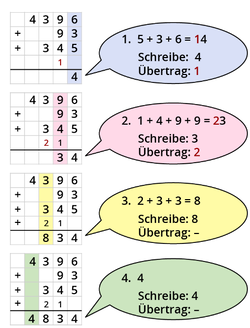
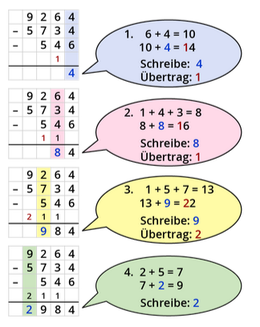
Addition von natürlichen Zahlen
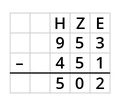
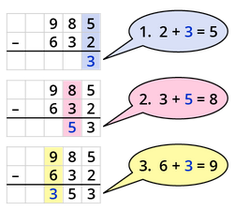
Subtraktion von natürlichen Zahlen
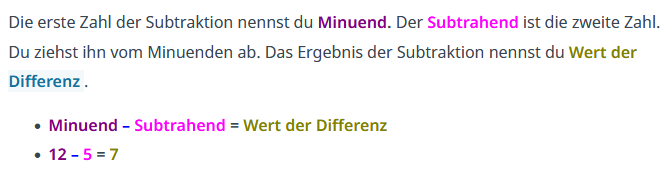
Fachbegriffe und Rechengesetze
Gemischte Aufgaben