Digitale Werkzeuge in der Schule/Wie Funktionen funktionieren/Quadratische Funktionen: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 23: | Zeile 23: | ||
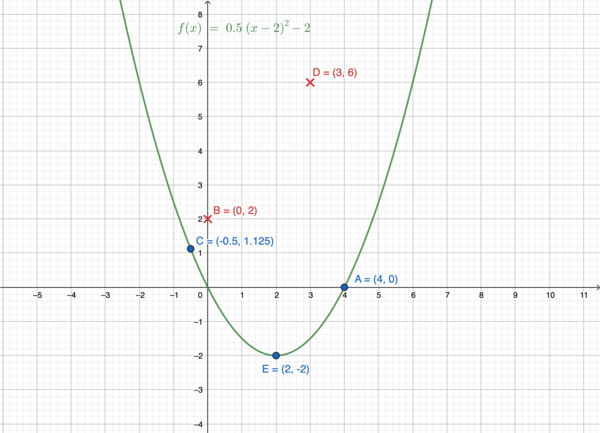
Gegeben sei die Funktion <math>f(x)=-0.5(x-2)^2-2</math><br /> | Gegeben sei die Funktion <math>f(x)=-0.5(x-2)^2-2</math><br /> | ||
Liegen folgende Punkte auf dem Graphen? | '''Liegen folgende Punkte auf dem Graphen? Zeichne den zugehörigen Graphen und die Punkte A-E in dein Heft.''' | ||
<math>A=(4,0)</math><br /><br /> | <math>A=(4,0)</math><br /><br /> | ||
| Zeile 33: | Zeile 33: | ||
{{Lösung versteckt| 1= Du kannst einfach prüfen, ob ein Punkt auf dem Graphen liegt: Setze den x-Wert in die Funktionsgleichung ein und berechne den zugehörigen y-Wert| 2=Tipp 1 | 3=schließen}} | {{Lösung versteckt| 1= Du kannst einfach prüfen, ob ein Punkt auf dem Graphen liegt: Setze den x-Wert in die Funktionsgleichung ein und berechne den zugehörigen y-Wert| 2=Tipp 1 | 3=schließen}} | ||
{{Lösung versteckt| 1= Du hast Probleme beim Zeichnen des Graphen? Der Lückentext in Aufgabe 1 hilft dir weiter.| 2=Tipp 2 | 3=schließen}} | {{Lösung versteckt| 1= Du hast Probleme beim Zeichnen des Graphen? Der Lückentext in Aufgabe 1 hilft dir weiter.| 2=Tipp 2 | 3=schließen}} | ||
Version vom 1. Mai 2019, 09:37 Uhr
Scheitelpunktform
Wir schauen uns die Funktion an. Funktionen dieser Art heißen qua dra tisch e Funktionen. Der Graph einer solchen Funktion ist eine Pa ra bel. Der höchste bzw. der tiefste Punkt eines solchen Funktionsgraphen heißt Schei tel punkt.
Ist der Parameter a kleiner als Null (a<0), dann ist der Graph der Funktion g nach un ten geöffnet.
Ist a größer als Null (<>0), dann ist der Graph von g nach o ben geöffnet.
Ist a größer als Eins (a>1) oder kleiner als minus Eins (a<-1), dann wird der Graph von g schma ler. Man sagt, dass in diesem Fall der Graph ge streckt wird.
Ist d größer als Null (d>0), dann wird der Graph von g nach rechts verschoben.
Ist d kleiner als Null (d<0), dann wird der Graph von g nach links verschoben.
Ist e kleiner als Null (e<0), dann wird der Graph von g nach un ten verschoben.
Ist e größer als Null (e>0), dann wird der Graph von g nach o ben verschoben.
Umwandlung Scheitelpunktform und Normalenform