Digitale Werkzeuge in der Schule/Wie Funktionen funktionieren/Quadratische Funktionen

Info

In diesem Lernpfad geht es darum, dein Wissen im Bereich quadratischer Funktionen zu vertiefen.

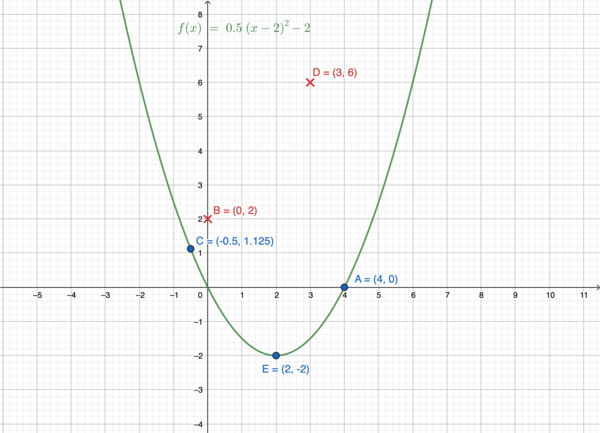
Scheitelpunktform

1. Parameter der Scheitelpunktsform

Fülle den folgenden Lückentext aus, indem du die passenden Silben einfügst.

Wir schauen uns die Funktion $g(x)=a*(x-d)^2+e$ an. Funktionen dieser Art heißen qua dra tisch e Funktionen. Der Graph einer solchen Funktion ist eine Pa ra bel. Der höchste bzw. der tiefste Punkt eines solchen Funktionsgraphen heißt Schei tel punkt.
Ist der Parameter a kleiner als Null (a<0), dann ist der Graph der Funktion g nach un ten geöffnet.
Ist a größer als Null (<>0), dann ist der Graph von g nach o ben geöffnet.
Ist a größer als Eins (a>1) oder kleiner als minus Eins (a<-1), dann wird der Graph von g schma ler. Man sagt, dass in diesem Fall der Graph ge streckt wird.

Ist d größer als Null (d>0), dann wird der Graph von g nach rechts verschoben.
Ist d kleiner als Null (d<0), dann wird der Graph von g nach links verschoben.

Ist e kleiner als Null (e<0), dann wird der Graph von g nach un ten verschoben.
Ist e größer als Null (e>0), dann wird der Graph von g nach o ben verschoben.

2. WANTED!

Gegeben sei die Funktion $f(x)=-0.5*(x-2)^2-2$
Liegen folgende Punkte auf dem Graphen?

$A=(4,0)$

$B=(0,2)$

$C=(-0.5, 1.125)$

$D=(3,6)$

$E=(2,-2)$

Zeichne den zugehörigen Graphen und die Punkte A-E in dein Heft.

3. Welcher Graph hat mit welcher Funktionsgleichung ein Match?

(Zuordnung Funktionsgraph und Funktionsgleichung.)

4. Aus dem Graphen eine quadratische Funktion in Scheitelpunktsform aufstellen

Umwandlung Scheitelpunktform und Normalenform

5. Die Umwandlungen zwischen Scheitelpunktform und Normalenform

Fülle den Lückentext aus, indem du auf eine Lücke klickst und die richtige Antwort auswählst.

6. Von der Scheitelpunktform zur Normalenform*

7. Wie ging noch einmal quadratische Ergänzung?*

8. Von der Normalenform zur Scheitelpunktform*

9. Finde die Paare

Wandle in deinem Heft die Funktionen f, g und h in die allgemeine Form um und die Funktionen i, j und k in die Scheitelpunktsform. Ordne anschließend die gleichen Funktionen einander zu.

Wenn du dir nicht mehr genau weißt, wie du von der Scheitelpunktform in die Normalform kommst oder umgekehrt, dann schau dir nochmal die Aufgaben 5, 6, 7 und 8 an.

10. würdest du bei der Umwandlung zwischen der Scheitelpunktform und der Normalform auch Millionär werden?**

Wähle die Antwortmöglichkeit A,B,C oder D, welche die angefangene Gleichung zu einer korrekten quadratischen Gleichung ergänzt.

Nullstellen

11. Nullstellen berechnen

Bestimme jeweils die Nullstellen:

$g(x)=-3(x-1)^2+3$

$h(x)=2x^2-8x+6$

Zur Erinnerung: Nullstellen sind diejenigen x-Werte, die eingesetzt in die Funktion "0" ergeben.

Setze zunächst $g(x)=0$ bzw. $h(x)=0$

Setze $g(x)=0$, d.h. $0 = -3(x-1)^2+3$ und teile dann beide Seiten durch $-3$

⇔ $0 = (x-1)^2-1$
⇔ $1 = (x-1)^2$

⇔ $x-1 = 1$ oder $x-1 = -1$

also folgt $x_1=2$ und $x_2=0$ und wir haben unsere Nullstellen gefunden.

Dieses mal könne wir die pq-Formel nutzen, um die Nullstellen zu bestimmen.

Setze $h(x)=0$, d.h. $0 = 2x^2-8x+6$ und teile dann beide Seiten durch $2$

$0 = x^2-4x+3$

Durch Anwenden der pq-Formel erhalten wir


⇔ $x_{1} = -\frac{-4}{2}-\sqrt{(\frac{-4}{2})^2-3}$ sowie $x_{2} = -\frac{-4}{2}+\sqrt{(\frac{-4}{2})^2-3}$

⇔ $x_1 = 2-1$ und $x_2 = 2+1$

also folgt $x_1=1$ und $x_2=3$ und wir haben unsere Nullstellen gefunden.

Anwendungsaufgabe

12. Baseball

Baseball ist eine der beliebtesten Sportarten der Welt. Beim Wurf erreicht der Ball Geschwindigkeiten bis zu 160km/h. Wenn der Schlagmann den Ball richtig trifft, kann dieser über die Tribüne hinweg aus dem Stadion fliegen. Ein bestimmter Schlag kann durch die Funktion
$j(x)=-0,0075x^2+1,2x+1$
beschrieben werden, wobei $x$ die horizontale Entfernung zum Schlagmann und $j(x)$ die Höhe des Balls, jeweils in Meter angibt.

a) Berechne j(0) und beschreibe, was dieser Wert im Anwendungskontext bedeutet.

Lies in der Aufgabenstellung noch einmal nach, wofür $x$ und $j(x)$ stehen.

Was bedeutet es, wenn x=0 ist?

b) Ein Spieler des gegnerischen Teams befindet sich 158 Meter vom Schlagmann entfernt in der Flugbahn des Balls. Wenn er hochspringt, erreichen seine Händen eine Höhe von 3,20 Metern. Berechne, ob der Spieler es schafft, den Balls aus der Luft zu fangen.

Berechne die Höhe des Balls nach 158 Metern und vergleiche diese Höhe mit der maximalen Sprunghöhe des Gegenspielers.

c) Berechne, wie weit der Baseball fliegt, wenn er von keinem gegnerischen Spieler aus der Luft gefangen wird.

Überlege dir, welchen Wert $j(x)$ annehmen muss, wenn der Baseball auf den Boden aufkommt.

Setze $j(x)=0$ und berechne die Nullstellen mithilfe der pq-Formel.

Falls du nicht mehr genau weißt, wie du die pq-Formel aufstellen und berechnen kannst, dann schau nochmal bei Aufgabe 11 nach. Achte darauf, dass vor dem $x^2$ kein Vorfaktor stehen darf.

d) Nach wieviel Metern erreicht der Baseball seine maximale Höhe? Welche Höhe erreicht er?

Überlege dir, an welchem Punkt der Flugkurve der Baseball am höchsten ist.

Gesucht ist der Scheitelpunkt von der Funktion. Überlege, wo du den Scheitelpunkt ablesen kannst.

Wenn du gerade nicht mehr darauf kommst, wie du aus der Normalform einer quadratischen Funktion in die Scheitelpunktsform kommst, dann guck dir nochmal die Aufgaben 5, 7 und 8 an.

Zusatzaufgabe** Berechne die horizontale Entfernung zum Schlagmann, in der der Baseball eine Höhe von 30 Metern hat.

Gesucht werden die x-Werte, sodass $j(x)=30$ ist.

Setze anstelle von $j(x)$ den Wert 30 in die Funktion ein und löse die Gleichung nach x auf.

Bringe alles auf eine Seite und berechne die Nullstellen.

a) [Lösung anzeigen][Lösung ausblenden]

$\begin{array}{rll} j(0) &=& -0.0075 \cdot 0^2 + 1.2 \cdot + 1 \\ &=& 1 \end{array}$

Der Schlagmann trifft den Baseball einen Meter über dem Boden.

b) [Lösung anzeigen][Lösung ausblenden]

$\begin{array}{rll} j(158) &=& -0.0075 \cdot 158^2+ 1.2 \cdot 158 + 1 \\ &=& 3.37 \end{array}$

Auf Höhe des gegnerischen Spielers hat der Baseball noch eine Höhe von $3.37m.$ Da der Spieler nur Bälle bis zu einer Höhe von $3.20m$ erreichen kann, fängt er diesen Ball nicht.

c) [Lösung anzeigen][Lösung ausblenden]

Nullstellenberechnung:
Im ersten Schritt wird der Vorfaktor von $x^2$ eliminiert.
$\begin{array}{rlll} 0 &=& -0.0075 \cdot x^2 + 1.2 \cdot x + 1 & \mid :(-0.0075) \\ &=& x^2 - 160x - \frac{400}{3} \end{array}$

Im zweiten Schritt wird die pq-Formel angewendet, um die Nullstellen zu berechnen.
$\Rightarrow p=-160, q= -\frac{400}{3}$
$\begin{array}{rlll} x_{1/2} &=& -\frac{-160}{2} \pm \sqrt{{\left( \frac{-160}{2} \right)}^2 -(-\frac{400}{3}} \\ &=& 80 \pm \sqrt{\frac{19600}{3}} \\ &=& 80 \pm 80.83 \\ \end{array}$
$\Rightarrow x_1 = 80+80.83 = 160.83$ und $x_2 = 80-80.83 = -0.83$

Da wir wissen möchten wie weit der Ball fliegt, wenn kein Gegenspieler ihn vorher fängt, müssen wir nur $x_1$ betrachten. Somit fliegt der Baseball $160.83$ Meter weit, bevor er auf dem Boden fällt.

d) [Lösung anzeigen][Lösung ausblenden]

Umwandlung der allgemeinen Form in die Scheitelpunktform:
$\begin{array}{rlll} j(x) &=& -0.0075 \cdot x^2 + 1.2 \cdot x +1 &\mid -0.0075 \, ausklammern \\ &=& -0.0075 (x^2-160x-\frac{400}{3}) &\mid +80^2 -80^2 \, quadratische \, Erg\ddot{a}nzung\\ &=& -0.0075 (x^2-160x + 80^2-80^2-\frac{400}{3}) &\mid 2. \, binomische \, Formel\\ &=& -0.0075 [(x-80)^2 -\frac{19600}{3}] &\mid ausmultiplizieren \\ &=& -0.0075 (x-80)^2 +49 \end{array}$

Der Scheitelpunkt liegt bei $S(80 \mid 49).$ Somit erreicht der Baseball nach $80$ Metern die maximale Höhe von $49$ Metern.

Zusatzaufgabe: [Lösung anzeigen][Lösung ausblenden]

Wir müssen für $j(x)=30$ die zugehörigen x-Werte berechnen. Dafür setzen wir $30$ für $j(x)$ ein und bringen als erstes alle Summanden auf eine Seite.
$30 = -0.0075 \cdot x^2 + 1.2 \cdot x + 1 \mid -30$ $\Leftrightarrow 0=-0.0075 \cdot x^2 + 1.2 \cdot x -29$

Als nächstes eliminieren wir den Vorfaktor vor $x^2.$
$\begin{array}{rlll} 0 &=& -0.0075 \cdot x^2 + 1.2 \cdot x -29 &\mid :(-0.0075) \\ &=& x^2 -160 \cdot x + \frac{11600}{3} \end{array}$

Nun lösen wir die Gleichung mithilfe der pq-Formel nach $x$ auf.
Es gilt $p=-160, q= \frac{11600}{3}.$
$\begin{array}{rll} x_{1/2} &=& -\frac{-160}{2} \pm \sqrt{ \left( \frac{-160}{2} \right)^2 - \frac{11600}{3}} \\ &=& 80 \pm \sqrt{\frac{7600}{3}}\\ &=& 80 \pm 50.33 \end{array}$
$\Rightarrow x_1 = 80+50.33 = 130.33$ und $x_2 = 80-50.33 = 29.67$

Der Baseball hat nach ungefähr $29.67$ Metern und nach ungefähr $130.33$ Metern eine Flughöhe von 30 Metern.