Digitale Werkzeuge in der Schule/Pyramiden entdecken/Pyramiden kennenlernen: Unterschied zwischen den Versionen
Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 79: | Zeile 79: | ||
Die Pyramide hat eine Grundfläche. Hinzu kommen 10 Seitenflächen. Insgesamt hat die Pyramide also '''11 Flächen'''.|2=Lösung zu d)|3=Lösung zu d)}} | Die Pyramide hat eine Grundfläche. Hinzu kommen 10 Seitenflächen. Insgesamt hat die Pyramide also '''11 Flächen'''.|2=Lösung zu d)|3=Lösung zu d)}} | ||
==7. | ==7. Besondere Formen== | ||
{{Box|1=Aufgabe 1: Besondere Pyramiden|2=Nachdem du dir die Definition einer Pyramide erarbeitet hast, kannst du dieses Wissen in der nächsten Aufgabe anwenden. Wechsle nun zu deinem Arbeitsblatt und bearbeite Aufgabe 7: Besondere Pyramiden.|3=Arbeitsmethode}} | |||
{{Lösung versteckt|1=Schaue dir die Grundfläche und die Seitenflächen des Körpers an.|2=Allgemeiner Tipp|3=Allgemeiner Tipp 2}} | |||
{{Lösung versteckt|1=Pyramiden haben ein Vieleck als Grundfläche und Dreiecke als Seitenflächen. Außerdem treffen sich die Seitenflächen in einem Punkt, die Spitze. Erfüllt der Körper diese Kriterien?|2=Allgemeiner Tipp|3=Allgemeiner Tipp 3}} | |||
{{Lösung versteckt|1=Bei dem Körper handelt es sich um eine Pyramide. Die Grundfläche ist ein Fünfeck und damit ein Vieleck. Der Körper wird von Dreiecken begrenzt. Außerdem treffen sich die Seitenflächen in einem Punkt. Diese Pyramide ist besonders, da sich die Spitze nicht über dem Mittelpunkt der Grundfläche befindet. Deshalb nennt man diese Pyramide eine '''schiefe Pyramide'''.|2=Lösung zu a)|3=Lösung zu a)}} | |||
{{Lösung versteckt|1=Bei dem Körper handelt es sich um eine '''Pyramide mit quadratischer Grundfläche'''. Außerdem bestehen die Seitenflächen aus Dreiecken, die sich in einem Punkt treffen. Das Besondere an dieser Pyramide ist, dass sie nicht auf ihrer Grundfläche steht, sondern auf einer Seitenfläche liegt.|2=Lösung zu b)|3=Lösung zu b)}} | |||
{{Lösung versteckt|1=Bei dem Körper handelt es sich nicht um eine Pyramide, da die Grundfläche ein Kreis und damit kein Vieleck ist. Außerdem sind die Seitenflächen keine Dreiecke. Dieser Körper ist ein '''Kegel'''.|2=Lösung zu c)|3=Lösung zu c)}} | |||
{{Lösung versteckt|1=Bei dem Körper handelt es sich um eine Pyramide. Die Grundfläche ist ein Sechseck und damit ein Vieleck. Außerdem bestehen die Seitenflächen aus Dreiecken, die sich in einem Punkt treffen. Da die Grundfläche unregelmäßig ist, spricht man von einer '''unregelmäßigen Pyramide'''.|2=Lösung zu d)|3=Lösung zu d)}} | |||
Version vom 27. Oktober 2022, 19:40 Uhr
Dieser Lernpfad befindet sich aktuell im Aufbau.
Pyramiden kennenlernen
In dem folgenden Lernpfad widmen wir uns dem mathematischen Körper der Pyramide.
In diesem Kapitel lernst du, ...
... wie du Pyramiden von anderen Körpern abgrenzt.
... wo Pyramiden in deinem Alltag überall auftauchen können.
... wie du eine Pyramide charakterisierst.
1. Memory
Als Start in die Welt der Pyramiden wiederholen wir noch einmal ein paar andere Körper, die du schon aus dem Matheunterricht kennst.
Wenn du merkst, dass du noch Schwierigkeiten hast, kannst du mit den anderen Apps das Thema Körper wiederholen!
2. Pyramiden im Alltag
Jetzt konzentrieren wir uns aber auf unser heutiges Thema, die Pyramiden. Zum Start überlegen wir, wo Pyramiden in unserem Alltag auftauchen können.
Schaue dir die folgenden Bilder von Pyramiden im Alltag an. Vielleicht kommen dir einige davon ja bekannt vor.
3. Tindern
Nun hast du schon einen ersten Eindruck, wie Pyramiden in der echten Welt aussehen können. Im folgenden Schritt wollen wir uns mathematischen besonderheiten des Körpers Pyramide nähern.
4. Skizze
Wir wollen uns nun Pyramiden genauer anschauen und die wichtigsten Begriffe erlernen.
5. Definition
Im nächsten Schritt erarbeiten wir die Definition einer Pyramide.
6. Tabelle
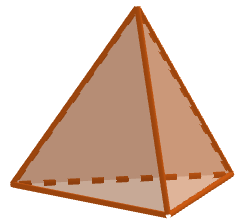
Die Grundfläche der Pyramide hat 3 Ecken. Hinzu kommt die Ecke der Spitze. Insgesamt hat die Pyramide somit 4 Ecken. Die Grundfläche der Pyramide hat 3 Kanten. Dazu kommen 3 Seitenkanten. Insgesamt hat die Pyramide also 6 Kanten.
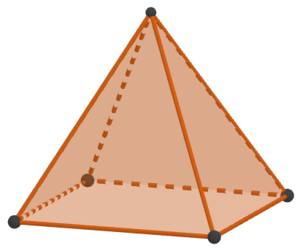
Die Pyramide hat eine Grundfläche. Hinzu kommen 3 Seitenflächen. Insgesamt hat die Pyramide also 4 Flächen.Hier siehst du eine Pyramide mit einem Viereck als Grundfläche. Bestimme die Anzahl der Ecken, Kanten und Flächen mithilfe der Abbildung.
Die Grundfläche der Pyramide hat 4 Ecken. Hinzu kommt die Ecke der Spitze. Insgesamt hat die Pyramide somit 5 Ecken. Die Grundfläche der Pyramide hat 4 Kanten. Dazu kommen 4 Seitenkanten. Insgesamt hat die Pyramide also 8 Kanten.
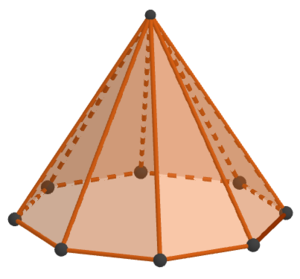
Die Pyramide hat eine Grundfläche. Hinzu kommen 4 Seitenflächen. Insgesamt hat die Pyramide also 5 Flächen.Die Grundfläche der Pyramide hat 8 Ecken. Hinzu kommt die Ecke der Spitze. Insgesamt hat die Pyramide somit 9 Ecken. Die Grundfläche der Pyramide hat 8 Kanten. Dazu kommen 8 Seitenkanten. Insgesamt hat die Pyramide also 16 Kanten.
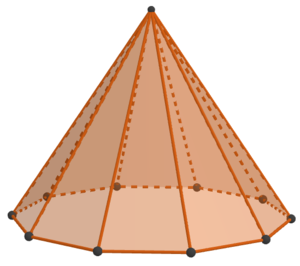
Die Pyramide hat eine Grundfläche. Hinzu kommen 8 Seitenflächen. Insgesamt hat die Pyramide also 9 Flächen.Die Grundfläche der Pyramide hat 10 Ecken. Hinzu kommt die Ecke der Spitze. Insgesamt hat die Pyramide somit 11 Ecken. Die Grundfläche der Pyramide hat 10 Kanten. Dazu kommen 10 Seitenkanten. Insgesamt hat die Pyramide also 20 Kanten.
Die Pyramide hat eine Grundfläche. Hinzu kommen 10 Seitenflächen. Insgesamt hat die Pyramide also 11 Flächen.