Benutzer:Buss-Haskert/Quadratische Funktionen/Scheitelpunktform: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 21: | Zeile 21: | ||
Und nun noch einmal schrittweise: | Und nun noch einmal schrittweise: | ||
===5.1 '''<big>D</big>'''etlef: f(x) = (x + '''<big><big><big>d</big></big></big>''')²=== | ====5.1 '''<big>D</big>'''etlef: f(x) = (x + '''<big><big><big>d</big></big></big>''')²==== | ||
Detlef ist ebenfalls sportlich, allerdings auch ein wenig '''<big><big><big>d</big></big></big>'''usselig. Er läuft beim Sprint immer in die entgegengesetzte Richtung. | Detlef ist ebenfalls sportlich, allerdings auch ein wenig '''<big><big><big>d</big></big></big>'''usselig. Er läuft beim Sprint immer in die entgegengesetzte Richtung. | ||
| Zeile 99: | Zeile 99: | ||
===5.2 '''<big>E</big>'''mil: f(x) = x² + '''<big><big><big>e</big></big></big>'''=== | ====5.2 '''<big>E</big>'''mil: f(x) = x² + '''<big><big><big>e</big></big></big>'''==== | ||
'''<big><big><big>e</big></big></big>'''mil ist ebenfalls sehr sportlich: | '''<big><big><big>e</big></big></big>'''mil ist ebenfalls sehr sportlich: | ||
| Zeile 167: | Zeile 167: | ||
===Verschobene Normalparabeln skizzieren/zeichnen ohne Schablone und ohne Wertetabelle=== | ===Verschobene Normalparabeln skizzieren/zeichnen ohne Schablone und ohne Wertetabelle=== | ||
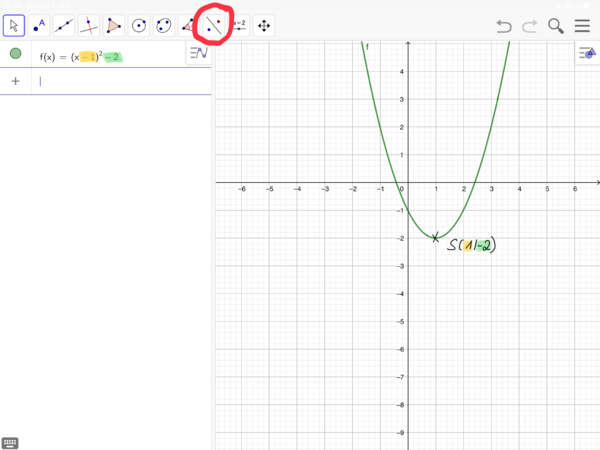
[[Datei:Idee Flipchart.png| | {{Box|Skizzieren einer verschobenen Normalparabel (ohne Schablone)|[[Datei:Idee Flipchart.png|rechts|rahmenlos|100x100px]] Um eine verschobene Normalparabel zu zeichnen, gehe vom Scheitelpunkt S aus immer eine Längeneinheit nach rechts und 1 Längeneinheit nach oben und dann 2 LE nach rechts und 4 LE nach oben, nutze danach die Achsensymmetrie der Parabel.<br> | ||
Das Applet zeigt das Skizzieren Schritt für Schritt. Erkläre!|Meinung}} | |||
<ggb_applet id="jn52gfzu" width="754" height="706" border="888888" /> | |||
<small>Applet von C.Buß-Haskert</small> | |||
Das Video erklärt dies noch einmal anschaulich. | |||
{{#ev:youtube|DeQRf1e4qZw|800|center|||start=0&end=89}} | {{#ev:youtube|DeQRf1e4qZw|800|center|||start=0&end=89}} | ||
<br> | <br> | ||
{{Box|1=Übung 18 - Parabeln skizzieren (ohne Schablone)|2=Skizziere wie oben beschrieben die verschobenen Normalparabeln ein deinem Heft. Zeichne in ein Koordinatenkreuz, nutze verschiedene Farben. | |||
* f(x) = (x-2)² + 1 | |||
* g(x) = (x+1)² + 2 | |||
* h(x) = (x-4)² - 1 | |||
* p(x) = (x+3)² - 2|3=Üben}} | |||
{{Box|Übung | {{Box|Übung 19 - Parablen skizzieren (online)|Bearbeite die Übungen aus dem GeoGebra-Applet, bis du sicher bist bei den Lösungen.|Üben}} | ||
<ggb_applet id="vmjjuqdt" width="827" height="526" border="888888" /> | <ggb_applet id="vmjjuqdt" width="827" height="526" border="888888" /> | ||
<br>Appelt von Wolfgang Wengler<br> | <br>Appelt von Wolfgang Wengler<br> | ||
{{Box|Übung | {{Box|Übung 20|Nachdem du die Aufgaben bis hier erfolgreich gelöst und diskutiert hast, sollten die nachfolgenden Aufgaben aus dem Buch kein Problem mehr für dich sein. | ||
* S.16 Nr. 4 | * S.16 Nr. 4 | ||
* S.16 Nr. 5 | * S.16 Nr. 5 | ||
| Zeile 202: | Zeile 212: | ||
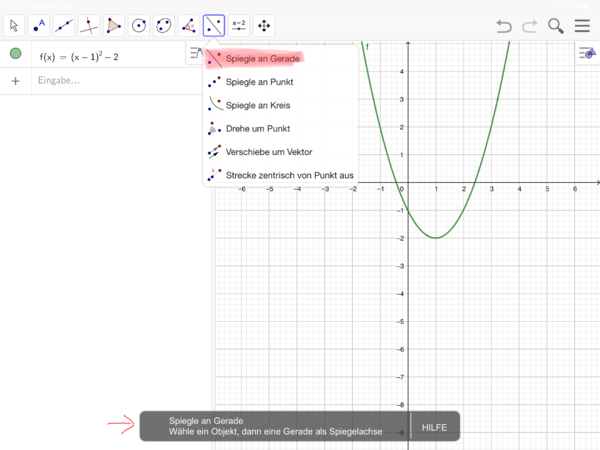
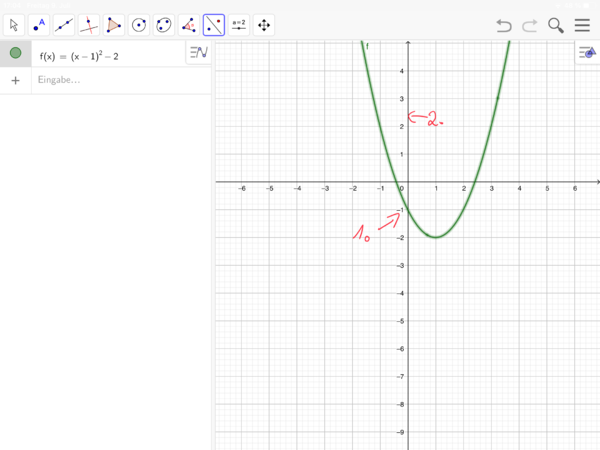
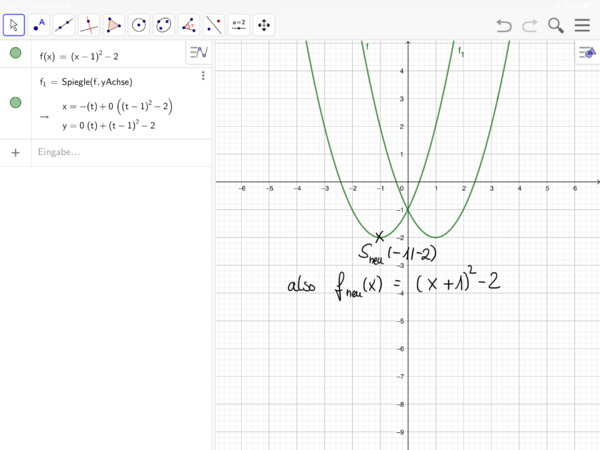
[[Datei:Verschobene Normalparabel spiegeln (GeoGebra) 4.png|rahmenlos|600x600px]]|zu Nr. 10: Spiegeln der verschobenen Normalparabel mithilfe von GeoGebra (Bilderfolge)|Verbergen}} | [[Datei:Verschobene Normalparabel spiegeln (GeoGebra) 4.png|rahmenlos|600x600px]]|zu Nr. 10: Spiegeln der verschobenen Normalparabel mithilfe von GeoGebra (Bilderfolge)|Verbergen}} | ||
{{Box|Übung | {{Box|Übung 21 - Punktprobe|Prüfe zeichnerisch (GeoGebra) und rechnerisch (Punktprobe), ob der Punkt P auf der Parabel liegt. | ||
* S. 16, Nr. 6|Üben}} | * S. 16, Nr. 6|Üben}} | ||
{{Lösung versteckt|1=Verschiebe den Scheitelpunkt passend zur Funktionsgleichung. Prüfe dann, ob der angegebene Punkt auf der Parabel liegt.<br> | {{Lösung versteckt|1=Verschiebe den Scheitelpunkt passend zur Funktionsgleichung. Prüfe dann, ob der angegebene Punkt auf der Parabel liegt.<br> | ||
Version vom 7. Juli 2022, 16:17 Uhr
SEITE IM AUFBAU
1 Quadratische Funktionen entdecken
2 Die Normalparabel f(x) = x²
3 Die gestreckte und gestauchte Parabel: Bedeutung des Parameters a in f(x) = ax²
4 Die verschobene Parabel: Bedeutung des Parameters c in f(x) = ax² + c
5 Die Scheitelpunktform quadratischer Funktionen f(x) = a(x+d)² + e
6 Die Normalform f(x) = x² + px + q und die allgemeine Form quadratischer Funktionen f(x) = ax² + bx + c
7 Nullstellen quadratischer Funktionen
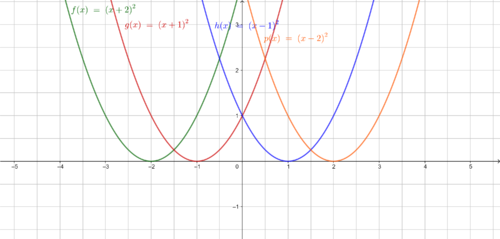
5 Scheitelpunktform quadratischer Funktionen

Und nun noch einmal schrittweise:
5.1 Detlef: f(x) = (x + d)²
Detlef ist ebenfalls sportlich, allerdings auch ein wenig dusselig. Er läuft beim Sprint immer in die entgegengesetzte Richtung.

5.2 Emil: f(x) = x² + e
emil ist ebenfalls sehr sportlich:
Er kann sehr hoch springen, ebenso gut kann er tauchen.


Die Scheitelpunktform quadratischer Funktionen f(x) = a(x+d)²+e
Nutze zur Lösungskontrolle das Applet. Schiebe den Scheitelpunkt S an den von dir angegebenen Punkt und schau, ob die Funktionsgleichung mit der im Buch angegebenen übereinstimmt

Nutze auch hier zur Lösungskontrolle das Applet. Verschiebe den Scheitelpunkt auf den im Buch angegeben Punkt und vergleiche die Funktionsgleichung mit deiner Lösung.

Originallink: https://www.geogebra.org/m/hgctdsff

Applet von Hans-Jürgen Elschenbroich
Originallink: https://www.geogebra.org/m/CdNTYBpZ


Applets von Wolfgang Wengler
Buch GeoGebra: Parabeln zeichnen
Originallink: https://www.geogebra.org/m/ZTXR23d8#chapter/236008




Applets von Bernhard Krügel
Verschobene Normalparabeln skizzieren/zeichnen ohne Schablone und ohne Wertetabelle

Applet von C.Buß-Haskert
Das Video erklärt dies noch einmal anschaulich.

Appelt von Wolfgang Wengler
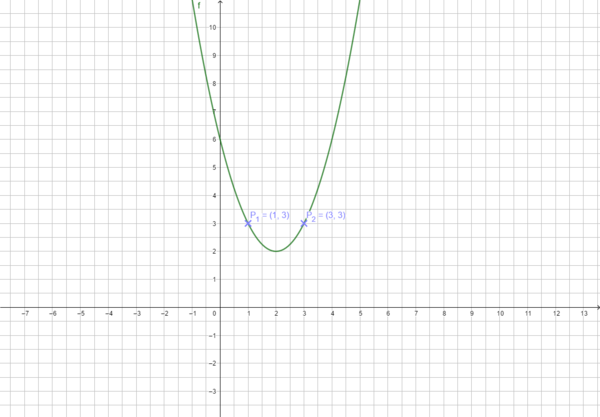
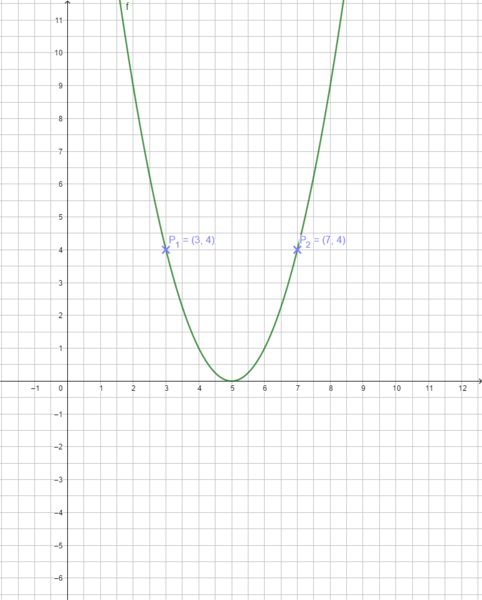
Nutze das Applet: Verschiebe den Scheitelpunkt so, dass der Graph durch die angegebene Punkte verläuft. Wo liegt dann der Scheitelpunkt? Begründe!

Nutze das Applet und verschiebe den Scheitelpunkt entsprechend der Angaben in der Aufgabe. Prüfe so deine Lösung.

Verschiebe den Scheitelpunkt passend zur Funktionsgleichung. Prüfe dann, ob der angegebene Punkt auf der Parabel liegt.

Rechnerische Probe: PUNKTPROBE
Musterlösung zu Aufgabenteil a)
f(x) = (x-4)²; P(1|9)
9 = (1-4)²
9 = (-3)²
9 = 9 (w)