Benutzer:Buss-Haskert/Quadratische Funktionen/Verschiebung entlang der y-Achse

SEITE IM AUFBAU

zurück zur Seite der Herta-Lebenstein-Realschule

Quadratische Funktionen - Startseite

1 Quadratische Funktionen entdecken
2 Die Normalparabel f(x) = x²
3 Die gestreckte und gestauchte Parabel: Bedeutung des Parameters a in f(x) = ax²
4 Die verschobene Parabel: Bedeutung des Parameters c in f(x) = ax² + c
5 Die Scheitelpunktform quadratischer Funktionen f(x) = a(x+d)² + e
6 Die Normalform f(x) = x² + px + q und die allgemeine Form quadratischer Funktionen f(x) = ax² + bx + c
7 Nullstellen quadratischer Funktionen

8 Modellieren (Anwendungsaufgaben)

4 Die verschobene Parabel: Bedeutung des Parameters c in f(x) = ax² + c

f(x) = ax² + c Bedeutung des Parameters c

Untersuche die Bedeutung des Parameters c in der Gleichung f(x) = ax² + c mithilfe der Geometriesoftware GeoGebra.

• Gib im Algebrafenster die Gleichung f(x) = x² ein. Es wird die Normalparabel gezeichnet.
• Erstelle einen Schieberegler a.
• Erstelle einen Schieberegler c.
• Gib im Algebrafenster die Gleichung f(x) = ax² + c ein. Verändere den Wert von c mithilfe des Schiebereglers. (Die Bedeutung des Parameters a hast du schon erarbeitet.)
• Wie verändert sich die Parabel? Notiere deine Beobachtungen.

Link zu GeoGebra

Falls du die Schieberegler nicht erstellen kannst, nutze das nachfolgende Applet.

Die verschobene Parabel: Bedeutung des Parameters c in f(x) = ax² + c

Der Graph der Funktion f(x) = ax² + c ist eine Parabel mit dem Scheitelpunkt S(0|c). Der Faktor a bestimmt die Öffnung und Form der Parabel, der Summand c verschiebt den Scheitelpunkt entlang der y-Achse.

Übung 8 - online

Bearbeite auf der Seite realmath so viele Aufgaben, bis mindestens 300 Punkte gesammelt hast.

• Parabeln zeichnen

Übung 9

Löse die Aufgaben aus dem Buch.

• S. 14 Nr. 10
• S. 14 Nr. 13
• S. 14 Nr. 14
• S. 14 Nr. 16 (Kontrolliere mit GeoGebra)

"Punktprobe"!

Setze die Koordinaten der Punkte in die Funktionsgleichungen ein und prüfe, ob eine wahre (w) Aussage oder falsche (f) Aussage entsteht. Demnach liegt der Punkt auf der Parabel bzw. nicht auf der Parabel.

Bilderfolge zu GeoGebra:

Übung 10: Modellieren mit quadratischen Funktionen

Datei:Modellieren.png

Löse die Aufgaben aus dem Buch. Erstelle eine Skizze und notiere deine Lösungen ausführlich und übersichtlich.

• S. 25 Nr. 5 (*)
• S. 25 Nr. 7 (**)
• S. 25 Nr. 8 (***)
• S. 25 Nr. 9 (**)

Alle Schaubilder sind entlang der y-Achse verschobene Parabeln, da die Gleichungen immer die Form f(x)=ax²+c haben. Skizziere jeweils die Parabel und überlege, welche Bedeutung die gesuchte Größe hat:

• Scheitelpunkt S (höchster/tiefster Punkt)
• Nullstellen N_1/N₂ (Schnittpunkte mit der x-Achse; also y = 0!)
• beliebiger Punkt auf der Parabel

Skizze: f(x) = 0,0125x² - 12
Die Parabel ist nach oben geöffnet, gestaucht (wegen 0,0125) und um 12 Einheiten entlang der y-Achse nach unten verschoben (wegen -12)

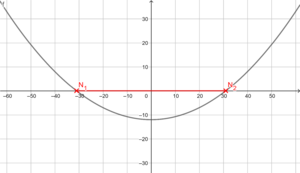
Der Durchmesser der Antenne entspricht dem Abstand zwischen den beiden Nullstellen N_{1 und} N₂.
Bestimme die Nullstellen: Dort gilt y = 0 !! (bzw. f(x) = 0)
0,0125x² - 12 = 0   |+12
0,0125x² = 12    |:0,0125
x² = 960     |$\surd$
x₁ = -30,98; x₂ = +30,98

Berechne nun den Durchmesser der Antenne.

Skizziere die Flugbahn des Balls so in ein Koordinatenkreuz, dass die Funktionsgleichung die Form f(x)=ax²+c hat. Der Scheitelpunkt liegt also auf der y-Achse!

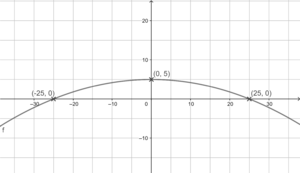
Die Funktionsgleichung hat die Form f(x)=ax²+c.
c=5 kannst du am Scheitelpunkt S(0|5) ablesen.

Bestimme nun a, indem du die Koordinaten einer Nullstelle N₁(-25|0) bzw. N₂(25|0) in die Funktionsgleichung einsetzt und nach a auflöst.

Sortiere in der LearningApp passend, was jeweils mathematisch gesucht ist.
Bearbeite danach die Aufgaben.

Das Applet zeigt die Flugbahn des Balls. Verschiebe den Punkt P auf der Parabel so, dass er zu den jeweiligen Fragestellungen passt. Welchen Punkt musst du zur Lösung der Aufgaben zunächst berechnen?
Originallink:https://www.geogebra.org/m/vtqcvs6s

gesucht: Höhe des Balls 1m nach dem Abschuss.
Zunächst musst du also die Abschussstelle berechnen, mathematisch ist dies die Nullstelle N₁.
Nullstellen berechnen: y = 0 !! (bzw. f(x) = 0)
-$\tfrac{1}{160}$x² + 4 = 0   |Löse die Gleichung
...
x₁≈-25,3; x₂≈25,3
Der x-Wert des Punktes 1m nach dem Abschuss ist also x = -24,3, also P(-24,3|___)
Bestimme nun rechnerisch die zugehörige y-Koordinate durch einsetzen von x = -24,3 in die Funktionsgleichung.

Prüfe mithilfe des Applets im vorherigen Tipp.

5 Scheitelpunktform quadratischer Funktionen