Digitale Werkzeuge in der Schule/Rund ums Dreieck/Besondere Dreiecke: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung |
|||
| Zeile 9: | Zeile 9: | ||
==Erkundung von Dreiecken== | ==Erkundung von Dreiecken== | ||
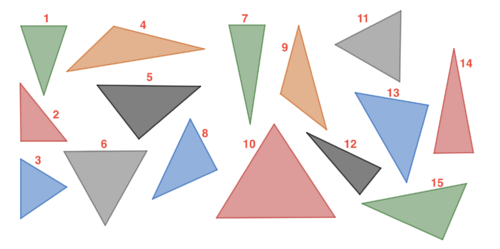
{{Box|1=Aufgabe 1: Erkundung von Dreiecken|2=In der Abbildung siehst du verschiedene Dreiecke. | {{Box|1=Aufgabe 1: Erkundung von Dreiecken|2=[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt''' | ||
In der Abbildung siehst du verschiedene Dreiecke. | |||
Tim hat bei den Dreiecken schon eine Gemeinsamkeit entdeckt. Findest du weitere? | Tim hat bei den Dreiecken schon eine Gemeinsamkeit entdeckt. Findest du weitere? | ||
Gib Dreiecke an die Gemeinsamkeiten haben und beschreibe diese Gemeinsamkeiten in wenigen Sätzen auf deinem Arbeitsblatt. (Hinweis: Du findest die Dreiecke auch auf deinem Arbeitsblatt in vergrößerter Form) | Gib Dreiecke an die Gemeinsamkeiten haben und beschreibe diese Gemeinsamkeiten in wenigen Sätzen auf deinem Arbeitsblatt. (Hinweis: Du findest die Dreiecke auch auf deinem Arbeitsblatt in vergrößerter Form) | ||
| Zeile 42: | Zeile 42: | ||
{{Box|1=Merksatz: Unterscheidung von Dreiecken mithilfe von Winkeln|2= | {{Box|1=Merksatz: Unterscheidung von Dreiecken mithilfe von Winkeln|2= | ||
[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt''' | |||
Vervollständige den Merksatz. (Hinweis: Wenn du dir unsicher bist, verschiebe in Aufgabe 3 noch einmal den Punkt und schau dir die Winkel genauer an) | Vervollständige den Merksatz. (Hinweis: Wenn du dir unsicher bist, verschiebe in Aufgabe 3 noch einmal den Punkt und schau dir die Winkel genauer an) | ||
| Zeile 49: | Zeile 51: | ||
Ein '''rechtwinkliges''' Dreieck hat einen rechten Winkel (genau 90°) und zwei spitze Winkel. | Ein '''rechtwinkliges''' Dreieck hat einen rechten Winkel (genau 90°) und zwei spitze Winkel. | ||
</div> | </div> | ||
Wenn du alle Lücken richtig ausgefüllt hast, schreibe den Merksatz auf dein Arbeitsblatt und beschrifte die abgebildeten Dreiecke. | Wenn du alle Lücken richtig ausgefüllt hast, schreibe den Merksatz auf dein Arbeitsblatt und beschrifte die abgebildeten Dreiecke. | ||
| Zeile 61: | Zeile 61: | ||
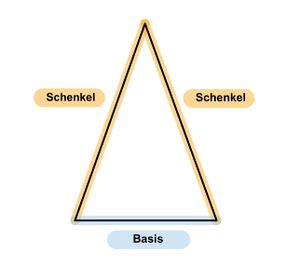
{{Box|1=Merksatz: Unterscheidung von Dreiecken mithilfe von Seitenlängen|2= | {{Box|1=Merksatz: Unterscheidung von Dreiecken mithilfe von Seitenlängen|2= | ||
[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt''' | |||
Vervollständige den Merksatz. Überlege wie die Dreiecke heißen könnten, wenn du zwischen einem Dreieck mit '''zwei''' gleichlangen Seiten und einem Dreieck mit '''drei''' gleichlangen Seiten unterscheiden möchtest. | Vervollständige den Merksatz. Überlege wie die Dreiecke heißen könnten, wenn du zwischen einem Dreieck mit '''zwei''' gleichlangen Seiten und einem Dreieck mit '''drei''' gleichlangen Seiten unterscheiden möchtest. | ||
| Zeile 73: | Zeile 75: | ||
|2=Tipp|3=Tipp verbergen.}} | |2=Tipp|3=Tipp verbergen.}} | ||
Wenn du alle Lücken richtig ausgefüllt hast, schreibe den Merksatz auf dein Arbeitsblatt und beschrifte die abgebildeten Dreiecke. | Wenn du alle Lücken richtig ausgefüllt hast, schreibe den Merksatz auf dein Arbeitsblatt und beschrifte die abgebildeten Dreiecke. | ||
| Zeile 101: | Zeile 100: | ||
{{LearningApp|width=100%|height=500px|app=p85hyw3ck22}}|3=Arbeitsmethode |Farbe={{Farbe|orange}}}} | {{LearningApp|width=100%|height=500px|app=p85hyw3ck22}}|3=Arbeitsmethode |Farbe={{Farbe|orange}}}} | ||
| Zeile 111: | Zeile 108: | ||
|3=Arbeitsmethode |Farbe=#CD2990}} | |3=Arbeitsmethode |Farbe=#CD2990}} | ||
{{Box|1=Aufgabe 4: Eigenschaften von Dreiecken|2= | {{Box|1=Aufgabe 4: Eigenschaften von Dreiecken|2= | ||
Version vom 16. Mai 2022, 12:28 Uhr
Erkundung von Dreiecken
Du kannst Dreiecke vergleichen, indem du ihre Winkel oder ihre Seitenlängen vergleichst.
Charakterisierungen von Dreiecken
Unterscheidung von Dreiecken mit Winkeln
Unterscheidung von Dreiecken mit Seitenlängen
Weiterführende Aufgaben
1. Ja, es kann gleichschenklig sein. Es ist ein Dreieck mit zweimal 45° Winkeln und einem rechten Winkel.
2. Ja, das stimmt. In einem gleichseitiges Dreieck sind alle Winkel 60°.
3. Das ist nicht wahr. Versuche mal ein Dreieck zu zeichnen, das einen stumpfen Winkel und einen rechten Winkel hat. Dann fällt dir vielleicht auf, dass das nicht möglich ist.