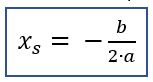|
|
| Zeile 4: |
Zeile 4: |
|
| |
|
| Seite im Aufbau! | | Seite im Aufbau! |
| | |
| | {{Navigation|[[Benutzer:L.hodankov/Quadratische Funktionen und Gleichungen üben|1 Die Scheitelpunktform quadratischer Funktionen f(x) = a(x+d)² + e]]<br> |
| | [[Benutzer:L.hodankov/Quadratische_Funktionen_üben/Normalform|2 Die Normalform f(x) = x² + px + q und die allgemeine Form quadratischer Funktionen f(x) = ax² + bx + c]]<br> |
| | [[Benutzer:L.hodankov/Quadratische Funktionen/Nullstellen|3 Nullstellen quadratischer Funktionen]]<br> |
| | [[Benutzer:L.hodankov/Quadratische Funktionen/Anwendungen|4 Modellieren (Anwendungsaufgaben)]]}} |
|
| |
|
| ===2 Die Normalform und die allgemeine Form quadratischer Funktionen=== | | ===2 Die Normalform und die allgemeine Form quadratischer Funktionen=== |
| Zeile 84: |
Zeile 89: |
| <br> | | <br> |
|
| |
|
| {{Fortsetzung|weiter=7 Nullstellen quadratischer Funktionen|weiterlink=Benutzer:Buss-Haskert/Quadratische Funktionen/Nullstellen}} | | {{Fortsetzung|weiter=3 Nullstellen quadratischer Funktionen|weiterlink=Benutzer:L.hodankov/Quadratische Funktionen/Nullstellen}} |
|
| |
|
|
| |
|
Version vom 9. März 2022, 23:19 Uhr
Diese Seite des Lernpfades wurde teilweise übernommen von der Seite Herta-Lebenstein-Realschule https://projekte.zum.de/wiki/Benutzer:Buss-Haskert/Quadratische_Funktionen. Der Autor ist Buss-Haskert. Diese Seite wurde veröffentlicht unter der Lizenz CC BY SA.
Herzlichen Dank!
Seite im Aufbau!
2 Die Normalform und die allgemeine Form quadratischer Funktionen
Eine Parabel, zwei Gleichungen...
Das nachfolgende GeoGebra-Applet zeichnet die Parabeln zu den Funktionsgleichungen. Erstelle eine Parabel in der Normalform und stelle anschließend e und f für die Scheitelpunktform so ein, dass die Graphen identisch sind.
Beschreibe deine Beobachtung.
Die Normalform quadratischer Gleichungen f(x) = x² + px + q und die allgemeine Form quadratischer Gleichungen f(x) = ax² + bx + c
Die quadratischen Funktionen der Form f(x) = x² + px + q haben die verschobene Normalparabel als Graphen.
Funktionen der Form f(x) = ax² + bx + c haben Parabeln als Graphen. Wandeln wir die Normalform bzw. die allgemeine Form in die Scheitelpunktform um, so lässt sich der Scheitelpunkt ablesen.
2.1 Von der Scheitelpunkform in die Normalform bzw. in die allgemeine Form
Eine Parabel, zwei Gleichungen
Stelle im Applet die Schieberegler so ein, dass die Graphen identisch sind. Z.B. d=-3; e=-4 und p=6; q=5. Begründe rechnerisch, dass die Gleichungen dieselbe Parabel beschreiben.

Scheitelpunktform:
f(x) = (x+3)² - 4 |Klammer auflösen: 1. binomische Formel
= x² + 6x + 9 - 4 |zusammenfassen
= x² + 6x + 5
Normalform: f(x) = x² + 6x + 5
Übung 1: Von der Scheitelpunktform zur Normalform - online
Löse so viele Aufgaben des nachfolgenden Applets, bis du dich beim Umwandeln sicher fühlst. Die Tipps helfen dir Schritt für Schritt zur Lösung.
Applet von Tinwing
Übung 2: Von der Scheitelpunktform in die allgemeine Form
Forme die Funktionsgleichung der Funktion in der Scheitelpunktform in die allgemeine Form f(x) = ax² + bx + c um.
Beispiel:
f(x) = 2(x+2)² - 1 |1. binomische Formel anwenden
= 2(x² + 4x + 4) - 1 |ausmultiplizieren 
= 2x² + 8x + 8 - 1
= 2x² + 8x + 7
a) f(x) = 2(x-1)² + 0,5
b) f(x) = -0,2(x + 3)² + 4
c) f(x) = 0,5(x - 4)² - 6
2.2 Von der Normalform in die Scheitelpunktform
Von der Normalform in die Scheitelpunktform
Stelle im Applet die Schieberegler erneut so ein, dass die Graphen identisch sind. Z.B. p=6; q=9 und d=-3;e=0. Erkennst du einen Zusammenhang?

Von der allgemeinen Form zur Scheitelpunktform
Die Funktionsgleichung f(x)=ax² + bx + c in der allgemeinen Form lässt sich mit der Formel
in die Scheitelpunktform f(x)=a(x + e)² + f umwandeln,
um die Koordinaten des Scheitelpunktes S(-e|f) abzulesen.

Merke
Lies a und b ab und berechne die x- Koordinate mit der Formel
Setze das Ergebnis in die Gleichung ein und berechne so die y-Koordinate des Scheitelpunktes.

Übung 3 - online: Normalform -> Scheitelpunktform
Löse so viele Aufgaben, bis zu mindestens 300 Punkte gesammelt hast.
Übung 4 - Von der Normalform in die Scheitelpunktform
Löse die Aufgaben vom Übungsblatt 4 aus dem Unterricht. Prüfe deine Ergebnisse, indem du die Parabeln mit dem Applet oben zeichnest. Sie müssen identisch sein.
2.3 Von der allgemeinen Form quadratischer Funktionen in die Scheitelpunktform
Sind Funktionsgleichungen quadratischer Funktionen in der allgemeinen Form f(x) = ax² + bx + c gegeben, kann auch hier in die Scheitelpunkform f(x) = a (x + e)² + f umgeformt und der Scheitelpunkt S(-e|f)abgelesen werden.
Übung 5: Von der allgemeinen Form in die Scheitelpunktform
Wandle die Funktionsgleichungen von der allgemeinen Form in die Scheitelpunktform um. Bestimme dafür zunächst die Koordinaten des Scheitelpunktes rechnerisch. Handelt es sich um einen Hoch- oder Tiefpunkt?
a) f(x) = 2x² + 4x + 2
b) f(x) -0,3x² + 0,9x + 1,2
c) f(x) = 0,5x² + 7x
Prüfe deine Lösung mit GeoGebra.
Übung 6 - online: allgemeine Form -> Scheitelpunktform
Löse so viele Aufgaben, bis zu mindestens 300 Punkte gesammelt hast.
IDEENSAMMLUNG
Modellieren
Aufgabe Basektball (mit Lösungsschritten)