|
|
| Zeile 88: |
Zeile 88: |
| ===Symmetriepunkt außerhalb einer Figur bestimmen=== | | ===Symmetriepunkt außerhalb einer Figur bestimmen=== |
| '''Bisher lag der Symmetriepunkt S immer innerhalb der Figur. Jedoch kann er auch außerhalb liegen.''' | | '''Bisher lag der Symmetriepunkt S immer innerhalb der Figur. Jedoch kann er auch außerhalb liegen.''' |
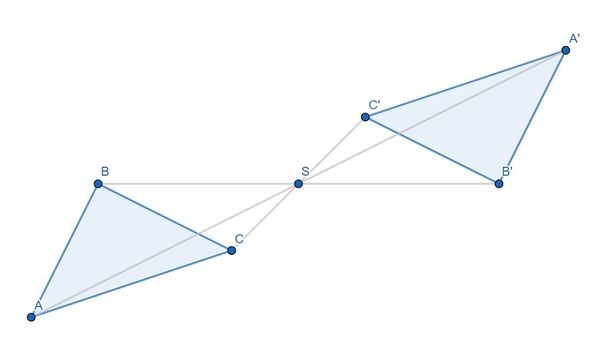
| [[Datei:Gespiegeltes Dreieck.jpg|mini|600px|Hier siehst du eine Figur mit ihrem Symmetriepunkt S, der außerhalb der Figur liegt.]] | | [[Datei:Gespiegeltes Dreieck.jpg|center|600px|]] |
| | Hier siehst du eine Figur mit ihrem Symmetriepunkt S, der außerhalb der Figur liegt |
|
| |
|
| {{Box | Aufgabe 5: Punktsymmetrie außerhalb der Figur | | | {{Box | Aufgabe 5: Punktsymmetrie außerhalb der Figur | |
Version vom 19. November 2021, 14:10 Uhr
Info
In diesem Lernpfadkapitel wirst du
- Punktsymmetrie kennenlernen,
- lernen punktsymmetrische Figuren zu erkennen
- und erfahren, wie du einen Symmetriepunkt bestimmst.
Bei den Aufgaben unterscheiden wir folgende Typen:
- In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
- Aufgaben in pinker Farbe sind Aufgaben mittlerer Schwierigkeit.
- Und Aufgaben mit lilanem Streifen sind Knobelaufgaben.
Viel Erfolg!
Einführung
Erdbeben im Museum
Aufgabe 1: Erdbeben im Museum
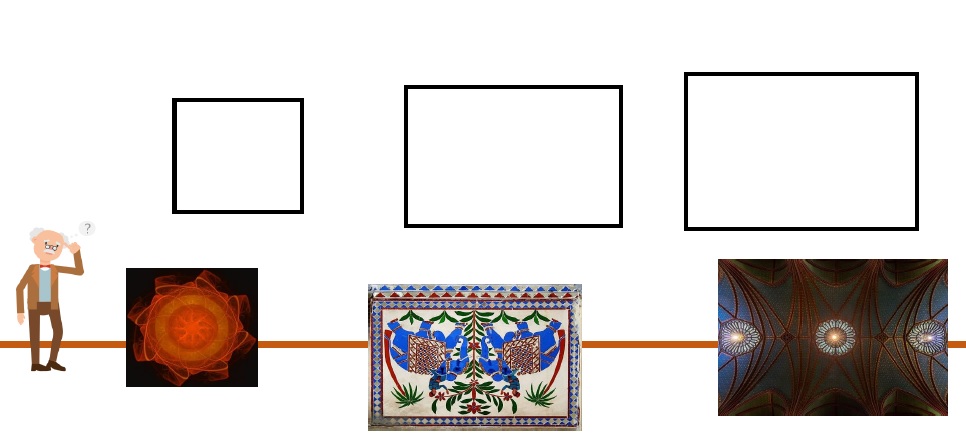
Im Kunstmuseum Münster gab es ein Erdbeben. Alle Werke sind dabei von den Wänden gefallen. Der Museumsdirektor ist verzweifelt, er weiß nicht wie sie aufgehängt waren. Hilf ihm, die Gemälde richtig aufzuhängen.
Schneide dazu die Bilder auf dem Arbeitsblatt aus und überlege, wie die Bilder aufgehängt werden können.
Beschreibe auf deinem Arbeitsblatt, was dir auffällt.
Kunstwerke auf den Kopf stellen
Aufgabe 2: Kunstwerke auf den Kopf stellen
Hier siehst du eine Reihe von Kunstwerken. Indem du die Schieberegler links neben den jeweiligen Kunstwerken von links nach rechts schiebst, kannst du die Kunstwerke um einen Punkt drehen, bis sie auf den Kopf stellen.
Beschreibe auf deinem Arbeitsblatt was sich verändert, wenn du die jeweiligen Kunstwerke auf den Kopf stellst.
Aufgabe 3: Tims Erkenntnis
Tim hat die Aufgaben auch gelöst, vergleiche deine Notizen mit seiner Erkenntnis.
Ordne die Kunstwerke danach, ob sich diese verändern oder gleich bleiben, nachdem du sie auf den Kopf stellst.
 Hinweis: Zum Überprüfen deiner Lösung drücke auf das blaue Häkchen.
Hinweis: Zum Überprüfen deiner Lösung drücke auf das blaue Häkchen.
Wir haben gesehen, dass einige Kunstwerke sich nicht verändern, wenn man sie auf den Kopf stellt.
Diese Entdeckung wollen wir nun mathematisch festhalten:
Merksatz - Punktsymmetrie
Wenn eine Figur auf den Kopf gedreht (180°-Drehung) genauso aussieht wie vorher, so nennt man sie punktsymmetrisch.
Der Punkt, um den du die Figur drehst, heißt Symmetriepunkt S.
Übungen
Symmetriepunkt überprüfen
Nicht alles lässt sich einfach so auf den Kopf stellen. Wie du in einem solchen Fall Punktsymmetrie trotzdem überprüfen kannst, lernst du mit der nächsten Aufgabe.
Methode: Punktsymmetrie überprüfen
Jede punktsymmetrische Figur hat einen Symmetriepunkt.
Um zu überprüfen, ob ein gewählter Punkt der Symmetriepunkt S ist, benötigst du ein Geodreieck. Lege dieses mit dem Nullpunkt an den vermuteten Symmetriepunkt an.
Haben zwei Punkte A und A' denselben Abstand zum Punkt S, so ist das der Symmetriepunkt und die Figur somit punktsymmetrisch.
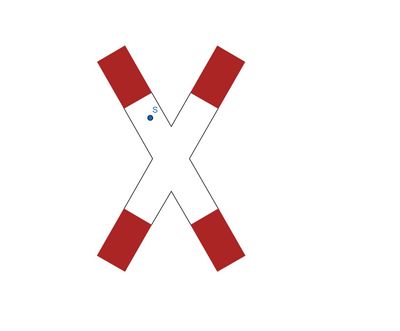
Ein Verkehrsschild mit einem markiertem Punkt, der der Symmetriepunkt sein könnte.
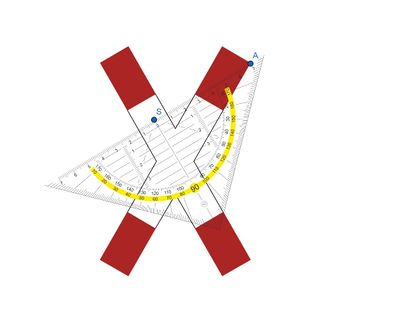
Nach Anlegen des Geodreiecks siehst du, dass der Punkt A keinen Spiegelpunkt auf der Figur hat. Deshalb kann der Punkt S nicht der Symmetriepunkt sein.
_________________________________________________________________________________________________________________________________
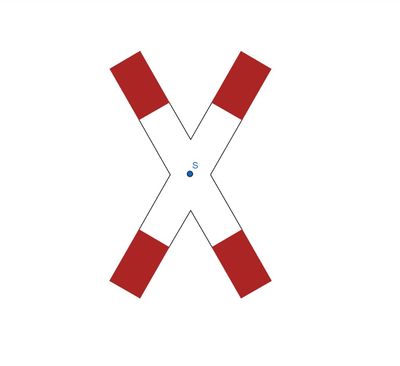
Wählen wir nun einen anderen Punkt, welcher der Symmetriepunkt sein könnte.
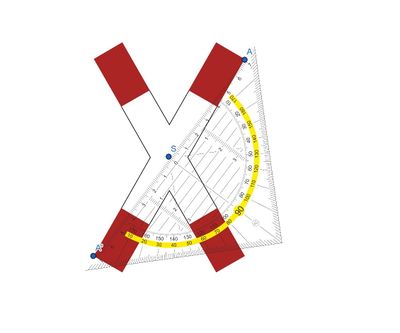
Mit dem angelegten Geodreieck erkennt man, dass die Punkte A und A' denselben Abstand zum Punkt S haben (7cm). Also ist der Punkt S der Symmetriepunkt.
Aufgabe 4: Punktsymmetrie mit dem Geodreieck erkennen
Bestimme bei den Bildern auf dem Arbeitsblatt mit dem Geodreieck, welcher der eingezeichneten Punkte der Symmetriepunkt ist.
Mithilfe des versteckten Applets kannst du überprüfen, ob deine Lösung richtig ist.
Klicke einfach auf das Bild und dann die richtige Farbe an.
 Hinweis: Indem du auf das Bild klickst, kannst du es vergrößern.
Hinweis: Indem du auf das Bild klickst, kannst du es vergrößern.
Bild 1: Grüner Punkt
Bild 2: Blauer Punkt
Bild 3: Roter Punkt
Bild 4: Grüner Punkt
Bild 5: Blauer Punkt
Bild 6: Roter Punkt
_________________________________________________________________________________________________________________________________
Symmetriepunkt außerhalb einer Figur bestimmen
Bisher lag der Symmetriepunkt S immer innerhalb der Figur. Jedoch kann er auch außerhalb liegen.
Hier siehst du eine Figur mit ihrem Symmetriepunkt S, der außerhalb der Figur liegt
Aufgabe 5: Punktsymmetrie außerhalb der Figur
Bestimme den Symmetriepunkt mithilfe der obengenannten Methode.
Auf deinem Arbeitsblatt kannst du die Methode anwenden.
Info
Super, du hast alle Aufgaben bearbeitet.
Du kennst jetzt
- die zentralen Merkmale von punktsymmetrischen Figuren
- und das Verfahren, wie du einen Symmetriepunkt innerhalb und außerhalb einer Figur bestimmen kannst.