Benutzer:Buss-Haskert/Quadratische Funktionen/Modellieren: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
K (Tipps) Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 96: | Zeile 96: | ||
Skizze: <br> | Skizze: <br> | ||
[[Datei:SP 10 S.25 Nr.6c Skizze.png|rahmenlos]]|Tipp zu Nr. 6c|Verbergen}} | [[Datei:SP 10 S.25 Nr.6c Skizze.png|rahmenlos]]|Tipp zu Nr. 6c|Verbergen}} | ||
{{Lösung versteckt|1=Die Sprungweite entspricht der 2. Nullstelle, also f(x) = 0.<br> | |||
Vergleiche deine rechnerische Lösung mit der tatsächlichen Sprungweite von 8,90m.|2=Tipp zu 6e|3=Verbergen}} | |||
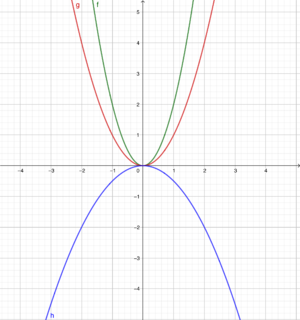
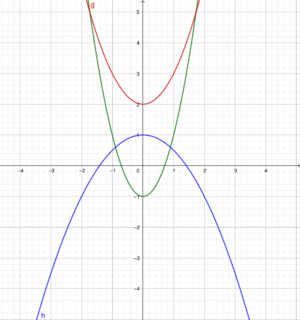
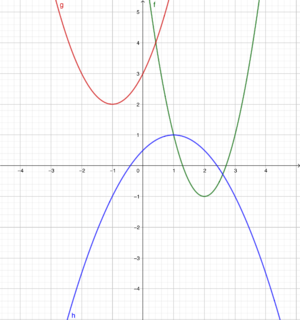
{{Lösung versteckt|Du hast zwei Möglichkeiten, die Flugbahn zu skizzieren:<br> | {{Lösung versteckt|Du hast zwei Möglichkeiten, die Flugbahn zu skizzieren:<br> | ||
[[Datei:SP 10 S.25 Nr.7 Skizzen.png|rahmenlos|600x600px]]<br> | [[Datei:SP 10 S.25 Nr.7 Skizzen.png|rahmenlos|600x600px]]<br> | ||
Die Lage des Scheitelpunktes entscheidet über die Form der Funktionsgleichung. Stelle jeweils die Funktionsgleichung auf und setzte die Koordinaten des Scheitelpunktes ein. Dann kannst du die Gleichung nach dem Parameter a auflösen.|Tipp zu Nr. 7 (2 mögliche Skizzen)|Verbergen}} | Die Lage des Scheitelpunktes entscheidet über die Form der Funktionsgleichung. Stelle jeweils die Funktionsgleichung auf und setzte die Koordinaten des Scheitelpunktes ein. Dann kannst du die Gleichung nach dem Parameter a auflösen.|Tipp zu Nr. 7 (2 mögliche Skizzen)|Verbergen}} | ||
{{Lösung versteckt|1=Die Funktionsgleichung hat die Form f(x) = ax² + c, daraus ergibt sich folgende Skizze:<br> | |||
[[Datei:SP10 S.25 Nr.8 Skizze.png|rahmenlos|600x600px]]|2=Tipp zu Nr. 8 (Skizze)|3=Verbergen}} | |||
{{Lösung versteckt|Skizze:<br> | |||
[[Datei:SP10 Nr.8a Skizze.png|rahmenlos|600x600px]]<br> | |||
Bestimme also zunächst die Nullstellen (f(x) = 0), gehe von dort aus 1m weiter nach rechts und bestimme für diese Stelle den zugehörigen y-Wert.<br> | |||
Lösung: P(-24,3|0,31), beantworte nun die Frage...|2=Tipp zu Nr. 8a|3=Verbergen}} | |||
{{Box|Übung 4 - online|Bearbeite auf der Seite [https://mathe.aufgabenfuchs.de/funktion/quadratische-funktion.shtml Aufgabenfuchs] die Aufgabe | {{Box|Übung 4 - online|Bearbeite auf der Seite [https://mathe.aufgabenfuchs.de/funktion/quadratische-funktion.shtml Aufgabenfuchs] die Aufgabe | ||
* 11|Üben}} | * 11|Üben}} | ||
Version vom 17. Oktober 2021, 10:23 Uhr
SEITE IM AUFBAU
1 Quadratische Funktionen entdecken
2 Die Normalparabel f(x) = x²
3 Die gestreckte und gestauchte Parabel: Bedeutung des Parameters a in f(x) = ax²
4 Die verschobene Parabel: Bedeutung des Parameters c in f(x) = ax² + c
5 Die Scheitelpunktform quadratischer Funktionen f(x) = a(x+d)² + e
6 Die Normalform f(x) = x² + px + q und die allgemeine Form quadratischer Funktionen f(x) = ax² + bx + c
7 Nullstellen quadratischer Funktionen
8 Modellieren - Anwendungsaufgaben
In unserer Umgebung gibt es viele Beispiele für Parabeln. Besonders häufig sind sie z.B. beim Brückenbau und bei Wurf- bzw. Flugbahnen zu sehen.
Es gibt besondere Punkte, die in Anwendungen immer wieder von Bedeutung sind:
- Scheitelpunkt
- Nullstellen
- Schnittpunkt mit der y-Achse
- Koordinaten eines beliebigen Punktes
Wenn in Anwendungsaufgaben die Funktionsgleichung gegeben ist, schau, welche Form sie hat, zeichne eine passende Skizze, beschrifte die Achsen und trage gegebene Punkte ein.
(Autor:Roulex 45; https://de.wikipedia.org/wiki/Golden_Gate_Bridge#/media/Datei:Golden-Gate-Bridge.svg)
Mögliche Fragen sind:
- Wie hoch verläuft die Fahrbahn über dem Meeresspielgel? (Scheitelpunkt, y-Koordinate)
- Wie lang sind die Hängeseile? (Koordinaten bestimmter Punkte auf der Parabel)
Mögliche Fragen sind:
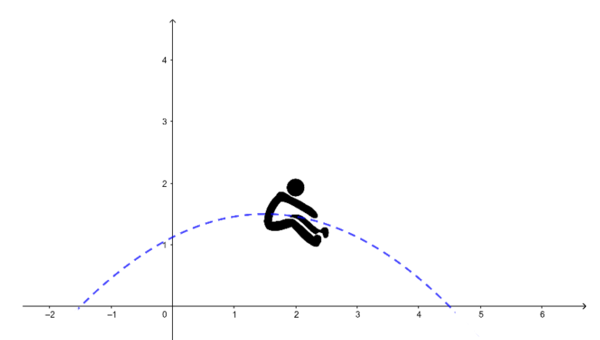
- Wie weit springt die Person? (2. Nullstelle)
- Wann hat sie die größte Sprunghöhe erreicht? (x-Koordinate des Scheitelpunktes)
- Wie hoch ist die größte Höhe des Körperschwerpunktes? (y-Koordinate des Scheitelpunktes)
- Wie hoch liegt der Körperschwerpunkt beim Absprung über dem Boden? (Schnittpunkt mit der y-Achse)
Tipp: Skizze!
Zeichne das Koordinatensystem so ein, dass der Scheitelpunkt S im Ursprung liegt. Dann kannst du die Funktionsgleichung der Form f(x) = ax² nutzen.
Beschrifte die Skizze mit den gegebenen Größen.
Koordinatenkreuz passend eingetragen:
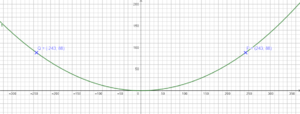
Die Spannweite w=486m und die Höhe h=88m führt zu den Punkten P(243|88) und Q(-243|88). Setze die Koordinaten passend in die Funktionsgleichung f(x) = ax² ein und löse nach a auf.
Es können die Punkte P(-23,5|-6,6), Q(-17|-6,5), R(-10,5|-1,3) und S(0|0) abgelesen werden. Die Koordinaten von P eingesetzt in die Funktionsgleichung f(x) = ax² ergeben für a den Wert a=≈-0,012.
Bestimme a mithilfe des Punktes Q: a=≈-0,012.
Bestimme a mithilfe des Punktes R: a=≈-0,012.
Die Spannweite beträgt w=158m, die Höhe h=69m. Daher kennst du die Punkte P(-79|-69) und Q(79|-69)
Setze die Koordianten in die Funktionsgleichung ein und prüfe, ob du a=- erhältst.
ODER
Setze die x-Koordiante eines Punktes in die Funktionsgleichung ein und prüfe, ob die berechnete y-Koordinate passt.
Skizze: Die Funktionsgleichung hat die Form f(x) = ax² + c, verläuft also symmetrisch zur y-Achse.
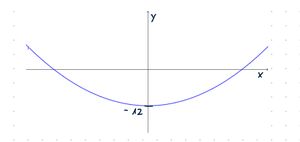
Welche mathematische Bedeutung hat der Durchmesser? Gesucht ist der Abstand zwischen den Nullstellen.
Die Funktionsgleichung hat die Form f(x) = a(x + d)² + e, mit a=-0,05, also nach unten geöffnet und gestaucht und S(3|1,8). Skizze:
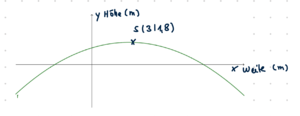
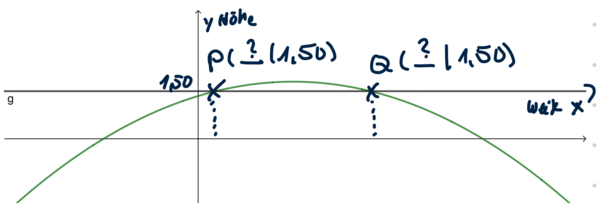
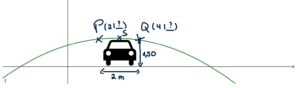
Erkundige dich, wie hoch und breit ein Auto ist. Zeichne es dann symmetrisch zum Scheitelpunkt in deine Skizze und überlege, welche Größen gesucht sind.
Skizze:
Die Sprungweite entspricht der 2. Nullstelle, also f(x) = 0.