Benutzer:Buss-Haskert/Quadratische Funktionen/Normalparabel: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
(Applet ergänzt) Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 44: | Zeile 44: | ||
(Falls du später den Taschenrechner benutzt, denke an die Klammer, falls die Zahl ein Minuszeichen als Vorzeichen hat.)<br> | (Falls du später den Taschenrechner benutzt, denke an die Klammer, falls die Zahl ein Minuszeichen als Vorzeichen hat.)<br> | ||
{{Lösung versteckt|[ | {{Lösung versteckt|<ggb_applet id="cn4fsvwn" width="1080" height="790" border="888888" /> | ||
Link, falls das Applet nicht richtig dargestellt wird: [https://www.geogebra.org/m/cn4fsvwn]|Hilfe zum Schaubild|Verbergen}} | |||
{{Lösung versteckt|1=Fülle den Lückentext aus.<br> | {{Lösung versteckt|1=Fülle den Lückentext aus.<br> | ||
{{LearningApp|app=prohah15a20|width=100%|height=900px}}|2=Hilfe zur Beschreibung der Normalparabel|3=Verbergen}} | {{LearningApp|app=prohah15a20|width=100%|height=900px}}|2=Hilfe zur Beschreibung der Normalparabel|3=Verbergen}} | ||
Version vom 21. August 2021, 09:02 Uhr
SEITE IM AUFBAU
1 Quadratische Funktionen entdecken
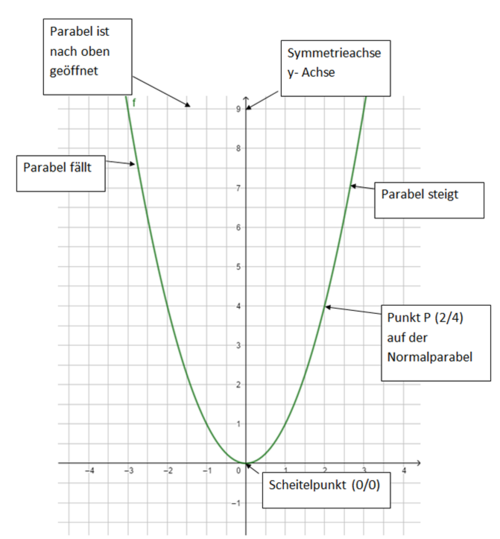
2 Die Normalparabel f(x) = x²
3 Die gestreckte und gestauchte Parabel: Bedeutung des Parameters a in f(x) = ax²
4 Die verschobene Parabel: Bedeutung des Parameters c in f(x) = ax² + c
5 Die Scheitelpunktform quadratischer Funktionen
2 Die Normalparabel
Erinnerung: (-2)² = (-2)·(-2) = +4
(Falls du später den Taschenrechner benutzt, denke an die Klammer, falls die Zahl ein Minuszeichen als Vorzeichen hat.)

Fülle den Lückentext aus.
Du kannst mithilfe des Schaubildes (Normalparabel) entscheiden, welche Punkte auf der Normalparabel liegen und welche nicht:
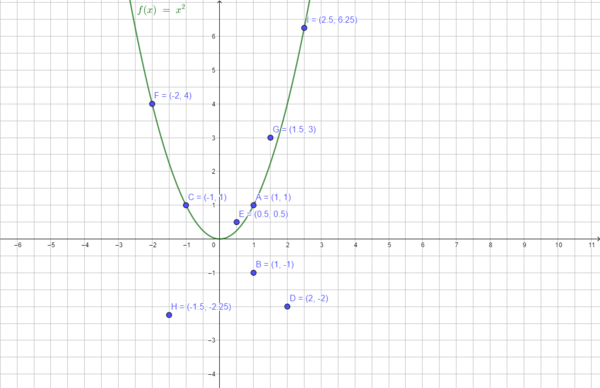
Wie kannst du rechnerisch prüfen, ob ein Punkt auf der Normalparabel liegt oder nicht?
Beispiel:
Liegt der Punkt I(2,5|6,25) auf der Normalparabel?
f(x) = x²
6,25 = 2,5²
6,25 = 6,25 (w), also liegt der Punkt I auf der Normalparabel.
Liegt der Punkt H(-1,5|-2,25) auf der Normalparabel?
f(x) = x²
-2,25 = (-1,5)²
-2,25 = 2,25 (f), also liegt der Punkt H nicht auf der Normalparabel.
Beispiel:
Bestimme die fehlende Koordinate von P(6|__) auf der Normalparabel.
f(x) = x²
y = 6²
y = 36, also P(6|36)
Bestimme die fehlende Koordinate von Q(__|1,69) auf der Normalparabel.
f(x) = x²
1,69 = x² |
= x
1,3 = x1; -1,3 = x2, also lautet Q1(1,3|1,69) und Q2(-1,3|1,69).
Es gibt zwei Punkte, die den y-Wert 1,69 haben, denn die Normalparabel ist symmetrisch zur y-Achse.