Benutzer:Buss-Haskert/Quadratische Funktionen/Scheitelpunktform: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
K (Übungsapplet ergänzt) Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 38: | Zeile 38: | ||
<br> | <br> | ||
{{Box|Übung 8|Nachdem du die Aufgaben auf der Seite realmath erfolgreich gelöst und diskutiert hast, sollten die nachfolgenden Aufgaben aus dem Buch kein Problem mehr für dich sein. | {{Box|Übung 8 - online|Bearbeite die Übungen aus dem GeoGebra-Applet, bis du sicher bist bei den Lösungen.|Üben}} | ||
<ggb_applet id="vmjjuqdt" width="827" height="526" border="888888" /> | |||
<br>Appelt von Wolfgang Wengler<br> | |||
{{Box|Übung 9|Nachdem du die Aufgaben auf der Seite realmath erfolgreich gelöst und diskutiert hast, sollten die nachfolgenden Aufgaben aus dem Buch kein Problem mehr für dich sein. | |||
* S.16 Nr. 1 | * S.16 Nr. 1 | ||
* S.16 Nr. 2 | * S.16 Nr. 2 | ||
| Zeile 66: | Zeile 71: | ||
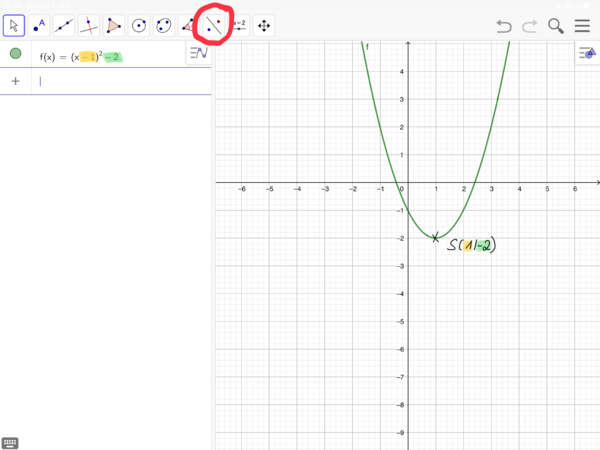
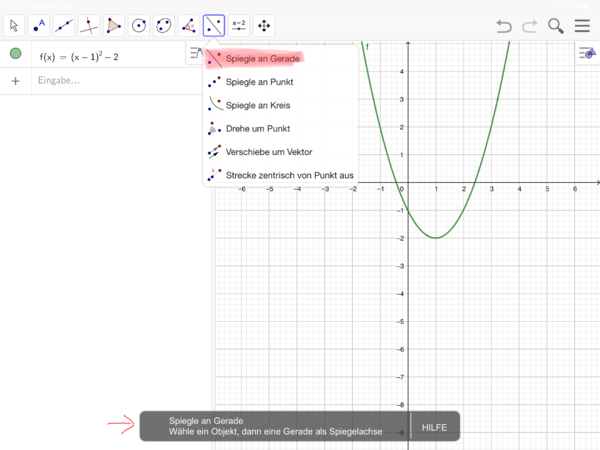
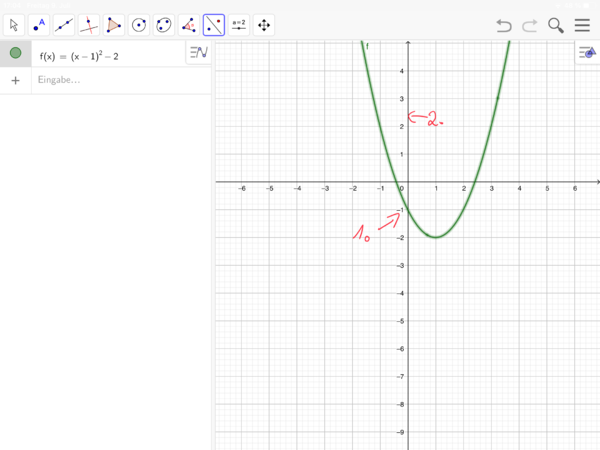
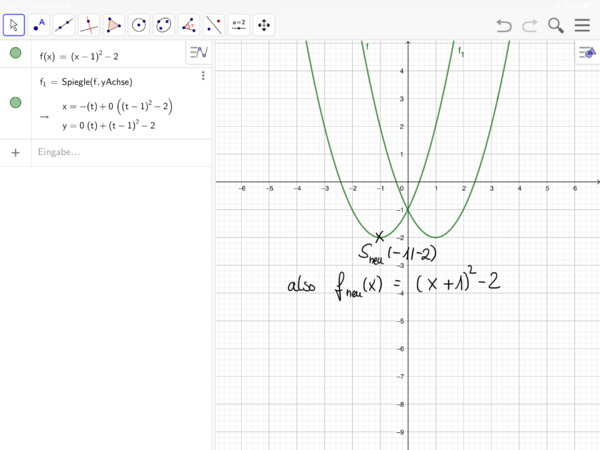
[[Datei:Verschobene Normalparabel spiegeln (GeoGebra) 4.png|rahmenlos|600x600px]]|zu Nr. 10: Spiegeln der verschobenen Normalparabel mithilfe von GeoGebra (Bilderfolge)|Verbergen}} | [[Datei:Verschobene Normalparabel spiegeln (GeoGebra) 4.png|rahmenlos|600x600px]]|zu Nr. 10: Spiegeln der verschobenen Normalparabel mithilfe von GeoGebra (Bilderfolge)|Verbergen}} | ||
{{Box|Übung | {{Box|Übung 10 - Punktprobe|Prüfe zeichnerisch (GeoGebra) und rechnerisch (Punktprobe), ob der Punkt P auf der Parabel liegt. | ||
* S. 16 Nr. 6|Üben}} | * S. 16 Nr. 6|Üben}} | ||
Version vom 13. September 2021, 17:11 Uhr
SEITE IM AUFBAU
Quadratische Funktionen - Startseite
1 Quadratische Funktionen entdecken
2 Die Normalparabel f(x) = x²
3 Die gestreckte und gestauchte Parabel: Bedeutung des Parameters a in f(x) = ax²
4 Die verschobene Parabel: Bedeutung des Parameters c in f(x) = ax² + c
5 Die Scheitelpunktform quadratischer Funktionen
5 Scheitelpunktform quadratischer Funktionen


Applet von Hans-Jürgen Elschenbroich
Verschobene Normalparabeln skizzieren/zeichnen ohne Schablone und ohne Wertetabelle:
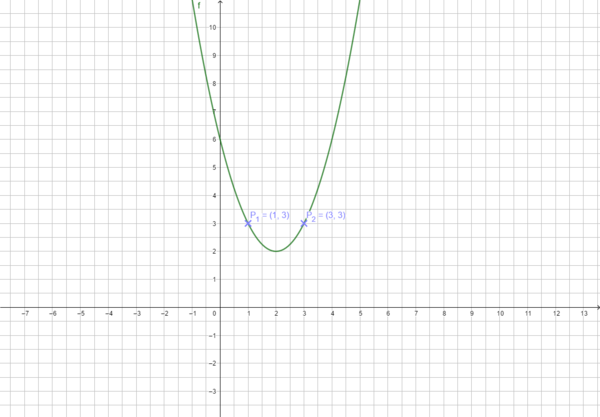
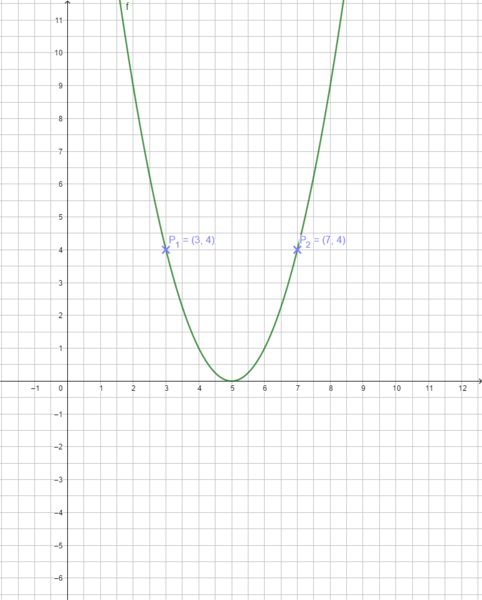
Um eine verschobene Normalparabel zu zeichnen, gehe vom Scheitelpunkt S aus immer eine Längeneinheit nach rechts und 1 Längeneinheit nach oben und dann 2 LE nach rechts und 4 LE nach oben. Das Video erklärt dies noch einmal anschaulich.

Appelt von Wolfgang Wengler
Nutze zur Lösungskontrolle das obige Applet. Schiebe den Scheitelpunkt S an den von dir angegebenen Punkt und schau, ob die Funktionsgleichung mit der im Buch angegebenen übereinstimmt.
Nutze auch hier zur Lösungskontrolle das obige Applet. Verschiebe den Scheitelpunkt auf den im Buch angegeben Punkt und vergleiche die Funktionsgleichung mit deiner Lösung.
Schau das Video oben noch einmal an und skizziere die verschobene Normalparabel vom Scheitelpunkt aus entsprechend.
Nutze das Applet oben: Verschiebe den Scheitelpunkt so, dass der Graph durch die angegebene Punkte verläuft. Wo liegt dann der Scheitelpunkt? Begründe!
Nutze das obige Applet und verschiebe den Scheitelpunkt entsprechend der Angaben in der Aufgabe. Prüfe so deine Lösung.