Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
K (Interne Links verschönert) Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 184: | Zeile 184: | ||
====⭐Ebene in Koordinatenform==== | ====⭐Ebene in Koordinatenform==== | ||
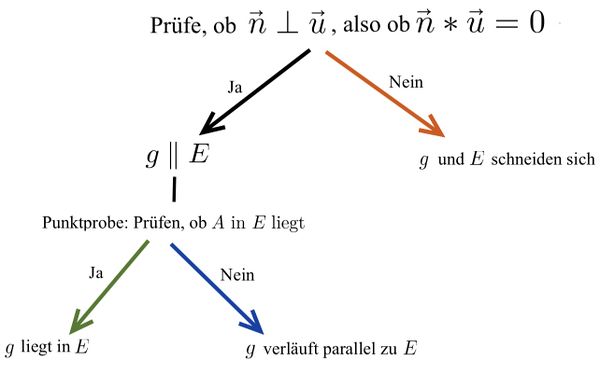
{{Box|⭐Merke: Die Lagebeziehung einer Gerade und einer Ebene mit dem Normalenvektor untersuchen|Bei der Bestimmung der Lagebeziehung zwischen einer Gerade <math>g</math> und einer Ebene <math>E</math> kann dir der Normalenvektor der Ebene helfen. | {{Box|⭐Merke: Die Lagebeziehung einer Gerade und einer Ebene mit dem Normalenvektor untersuchen|Bei der Bestimmung der Lagebeziehung zwischen einer Gerade <math>g</math> und einer Ebene <math>E</math> kann dir der Normalenvektor der Ebene helfen. | ||
Wenn du nicht mehr genau weißt, wie man diesen abliest oder berechnet, schau noch einmal in das Kapitel | Wenn du nicht mehr genau weißt, wie man diesen abliest oder berechnet, schau noch einmal in das Kapitel [[Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum|Ebenen im Raum]]. | ||
{{3Spalten | {{3Spalten | ||
| | | | ||
| Zeile 355: | Zeile 355: | ||
{{Lösung versteckt|1= Nutze zur Berechnung des Winkels die Formel aus dem Merksatz. Notiere dafür den Richtungsvektor der Gerade und den Normalenvektor der Ebene. | {{Lösung versteckt|1= Nutze zur Berechnung des Winkels die Formel aus dem Merksatz. Notiere dafür den Richtungsvektor der Gerade und den Normalenvektor der Ebene. | ||
Wenn du beide in die Formel eingesetzt hast, benötigst du den <math> | Wenn du beide in die Formel eingesetzt hast, benötigst du den <math>\sin^{-1}</math>, um den Winkel ausrechnen zu können. | ||
|2=Tipp anzeigen|3=Tipp verbergen}} | |2=Tipp anzeigen|3=Tipp verbergen}} | ||
| Zeile 368: | Zeile 368: | ||
'''3. Schritt''': Forme die Gleichung um. | '''3. Schritt''': Forme die Gleichung um. | ||
<math>\alpha = \ | <math>\alpha = \sin^{-1}(\frac{18}{\sqrt{1260}}) \Leftrightarrow \alpha \approx 28{,}45^{\circ}</math> | ||
Der Schnittwinkel beträgt also <math>28{,}45^{\circ}</math>. | Der Schnittwinkel beträgt also <math>28{,}45^{\circ}</math>. | ||
| Zeile 397: | Zeile 397: | ||
Mithilfe des Taschenrechners kann das Ergebnis berechnet werden: | Mithilfe des Taschenrechners kann das Ergebnis berechnet werden: | ||
<math>\alpha = \ | <math>\alpha = \sin^{-1}(\frac{1}{\sqrt{182}}) \Leftrightarrow \alpha \approx 21{,}75^{\circ}</math> | ||
Die Kinder sollten den Strohhalm also in einem Winkel von ca. <math>21{,}75^{\circ}</math> in das Trinkpäckchen stecken, um an den Saft in der gegenüberliegenden Ecke zu kommen. | Die Kinder sollten den Strohhalm also in einem Winkel von ca. <math>21{,}75^{\circ}</math> in das Trinkpäckchen stecken, um an den Saft in der gegenüberliegenden Ecke zu kommen. | ||
| Zeile 853: | Zeile 853: | ||
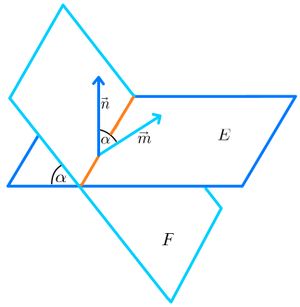
{{Box | ⭐ Merke: Berechnung des Winkel zwischen zwei Ebenen | | {{Box | ⭐ Merke: Berechnung des Winkel zwischen zwei Ebenen | | ||
Wenn sich zwei Ebenen schneiden, kann der Schnittwinkel bestimmt werden, den sie einschließen. Dazu kannst du die Normalenvektoren betrachten. Sie schließen denselben Winkel ein, wie die beiden Ebenen. Somit kann das Berechnen des Schnittwinkels zwischen zwei Ebenen auf das Berechnen des Winkels zwischen zwei Vektoren zurückgeführt werden. | Wenn sich zwei Ebenen schneiden, kann der Schnittwinkel bestimmt werden, den sie einschließen. Dazu kannst du die Normalenvektoren betrachten. Sie schließen denselben Winkel ein, wie die beiden Ebenen. Somit kann das Berechnen des Schnittwinkels zwischen zwei Ebenen auf das Berechnen des Winkels zwischen zwei Vektoren zurückgeführt werden. | ||
Um den Schnittwinkel zu berechnen, musst du zunächst die Normalenvektoren der Ebenen bestimmen. Wenn du nicht mehr genau weißt, wie das geht, schaue nochmal in Kapitel [[Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum|Ebenen im Raum]]. | Merksatz}} | Um den Schnittwinkel zu berechnen, musst du zunächst die Normalenvektoren der Ebenen bestimmen. Wenn du nicht mehr genau weißt, wie das geht, schaue nochmal in das Kapitel [[Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum|Ebenen im Raum]]. | Merksatz}} | ||
{{Box | ⭐ Merksatz: Formel zur Berechnung des Winkels zwischen zwei Ebenen | | {{Box | ⭐ Merksatz: Formel zur Berechnung des Winkels zwischen zwei Ebenen | | ||
| Zeile 877: | Zeile 877: | ||
'''3. Schritt:''' Auflösen der Gleichung. | '''3. Schritt:''' Auflösen der Gleichung. | ||
<math>\alpha = | <math>\alpha = \cos^{-1}(\frac{15}{3 \cdot \sqrt {59}}) \Leftrightarrow \alpha \approx 49{,}39^{\circ}</math> Der Winkel zwischen den Ebenen <math>E</math> und <math>F</math> beträgt ca. <math>49{,}39^{\circ}</math>.| Hervorhebung1}} | ||
| Zeile 898: | Zeile 898: | ||
Nun muss die Formel mit Hilfe des Taschenrechners aufgelöst werden: | Nun muss die Formel mit Hilfe des Taschenrechners aufgelöst werden: | ||
<math>\alpha = | <math>\alpha = \cos^{-1}(\frac{4}{\sqrt {56}}) \Leftrightarrow \alpha \approx 57{,}69^{\circ}</math> Der Winkel zwischen den Ebenen <math>E</math> und <math>F</math> beträgt ca. <math>57{,}69^{\circ}</math>. | ||
|2=Lösung anzeigen|3=Lösung verbergen}} | |2=Lösung anzeigen|3=Lösung verbergen}} | ||
| Zeile 914: | Zeile 914: | ||
Nun muss die Formel mit Hilfe des Taschenrechners aufgelöst werden: | Nun muss die Formel mit Hilfe des Taschenrechners aufgelöst werden: | ||
<math>\alpha = | <math>\alpha = \cos^{-1}(0) \Leftrightarrow \alpha = 90^{\circ}</math> Der Winkel zwischen den Ebenen <math>F</math> und <math>H</math> beträgt ca. <math>90^{\circ} </math>. | ||
|2=Lösung anzeigen|3=Lösung verbergen}} | |2=Lösung anzeigen|3=Lösung verbergen}} | ||
| Zeile 930: | Zeile 930: | ||
Nun muss die Formel mit Hilfe des Taschenrechners aufgelöst werden: | Nun muss die Formel mit Hilfe des Taschenrechners aufgelöst werden: | ||
<math>\alpha = | <math>\alpha = \cos^{-1}(\frac{7}{\sqrt {69}}) \Leftrightarrow \alpha \approx 32{,}57^{\circ}</math> Der Winkel zwischen den Ebenen <math>E</math> und <math>H</math> beträgt ca. <math>32{,}57^{\circ}</math>. | ||
|2=Lösung anzeigen|3=Lösung verbergen}} | |2=Lösung anzeigen|3=Lösung verbergen}} | ||
| Zeile 974: | Zeile 974: | ||
<math>\cos(\gamma)=\frac{\left| \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix} \ast \begin{pmatrix} 0\\ {-}1\\ 0{,}4 \end{pmatrix} \right|}{\left| \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 0\\ {-}1\\ 0{,}4 \end{pmatrix} \right|} \Leftrightarrow \cos(\gamma) = \frac{\frac{2}{5}}{1 \cdot \sqrt{\frac{29}{25}}}</math> | <math>\cos(\gamma)=\frac{\left| \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix} \ast \begin{pmatrix} 0\\ {-}1\\ 0{,}4 \end{pmatrix} \right|}{\left| \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 0\\ {-}1\\ 0{,}4 \end{pmatrix} \right|} \Leftrightarrow \cos(\gamma) = \frac{\frac{2}{5}}{1 \cdot \sqrt{\frac{29}{25}}}</math> | ||
Umstellen der Formel ergibt: <math> \gamma= | Umstellen der Formel ergibt: <math> \gamma=\cos^{-1} \left( \frac{\frac{2}{5}}{\sqrt{\frac{29}{25}}} \right) \Leftrightarrow \gamma \approx 68{,}2^{\circ}</math> | ||
Wie in der Abbildung zu sehen wurde der Winkel <math>\gamma</math> berechnet. Der Winkel zwischen der Sitzfläche und der Rückenlehne wird aber durch den Winkel <math>\alpha</math> beschrieben. <math>\alpha</math> erhält man, indem man <math>180^\circ - \gamma </math> berechnet: <math>180^{\circ} - 68{,}2^{\circ} = 111{,}8^{\circ}</math>. Mit einem Wert von <math> 111{,}8^{\circ}</math> liegt der Winkel zwischen Rückenlehne und Sitzfläche etwas über dem optimalen Winkel. |2=Lösung anzeigen|3=Lösung verbergen}} | Wie in der Abbildung zu sehen wurde der Winkel <math>\gamma</math> berechnet. Der Winkel zwischen der Sitzfläche und der Rückenlehne wird aber durch den Winkel <math>\alpha</math> beschrieben. <math>\alpha</math> erhält man, indem man <math>180^\circ - \gamma </math> berechnet: <math>180^{\circ} - 68{,}2^{\circ} = 111{,}8^{\circ}</math>. Mit einem Wert von <math> 111{,}8^{\circ}</math> liegt der Winkel zwischen Rückenlehne und Sitzfläche etwas über dem optimalen Winkel. |2=Lösung anzeigen|3=Lösung verbergen}} | ||
| Zeile 998: | Zeile 998: | ||
<math>\cos(\beta)=\frac{\left| \begin{pmatrix} 0\\ {-}1\\ 0{,}4 \end{pmatrix} \ast \begin{pmatrix} 0\\ {-}1\\ {-}0{,}4 \end{pmatrix} \right|}{\left| \begin{pmatrix} 0\\ {-}1\\ 0{,}4 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 0\\ {-}1\\ {-}0{,}4 \end{pmatrix} \right|} \Leftrightarrow \cos(\beta)=\frac{\frac{21}{25}}{\sqrt{\frac{29}{25}} \cdot \sqrt{\frac{29}{25}}} \Leftrightarrow \cos(\beta)=\frac{\frac{21}{25}}{\frac{29}{25}} \Leftrightarrow \cos(\beta)=\frac{21}{29}</math> | <math>\cos(\beta)=\frac{\left| \begin{pmatrix} 0\\ {-}1\\ 0{,}4 \end{pmatrix} \ast \begin{pmatrix} 0\\ {-}1\\ {-}0{,}4 \end{pmatrix} \right|}{\left| \begin{pmatrix} 0\\ {-}1\\ 0{,}4 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 0\\ {-}1\\ {-}0{,}4 \end{pmatrix} \right|} \Leftrightarrow \cos(\beta)=\frac{\frac{21}{25}}{\sqrt{\frac{29}{25}} \cdot \sqrt{\frac{29}{25}}} \Leftrightarrow \cos(\beta)=\frac{\frac{21}{25}}{\frac{29}{25}} \Leftrightarrow \cos(\beta)=\frac{21}{29}</math> | ||
Umstellen der Formel ergibt: <math> \beta= | Umstellen der Formel ergibt: <math> \beta=\cos^{-1} \left( \frac{21}{29} \right) \Leftrightarrow \beta \approx 43{,}6^{\circ} </math>. Der Winkel zwischen den beiden Rückenlehnen beträgt <math>43{,}6^{\circ} </math>.|2=Lösung anzeigen|3=Lösung verbergen}} | ||
| Arbeitsmethode | Farbe={{Farbe|grün}}}} | | Arbeitsmethode | Farbe={{Farbe|grün}}}} | ||
Aktuelle Version vom 23. Juni 2021, 23:28 Uhr
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
Untersuchung der Lagebeziehung zwischen Gerade und Ebene
Ebene in Parameterform
⭐Ebene in Koordinatenform
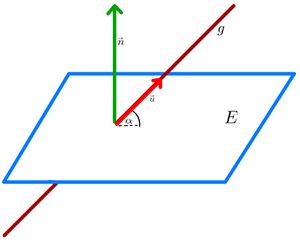
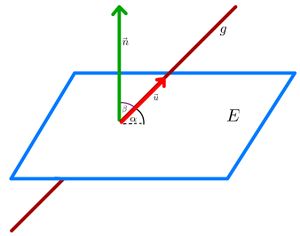
⭐Berechnung des Winkels zwischen Gerade und Ebene
Lagebeziehung Ebene-Ebene
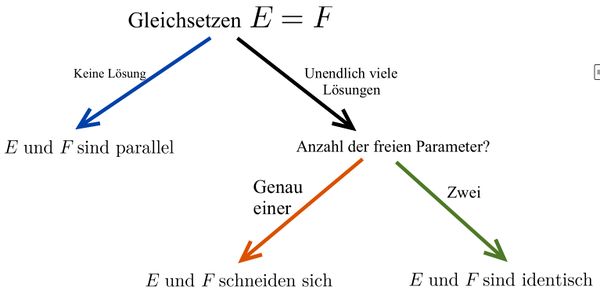
Mögliche Lagebeziehungen zwischen zwei Ebenen
Untersuchung der Lagebeziehung von zwei Ebenen
Beide Ebenengleichungen in Parameterform
⭐Ebenengleichungen in Parameter- und Koordinatenform
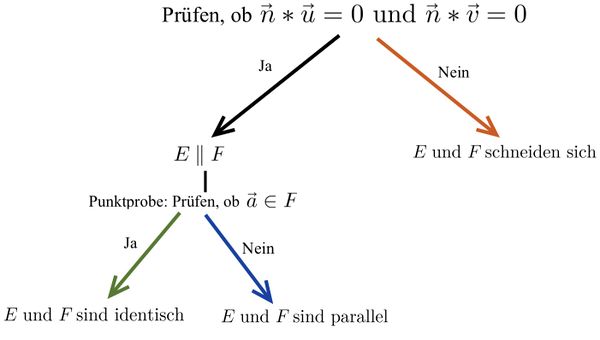
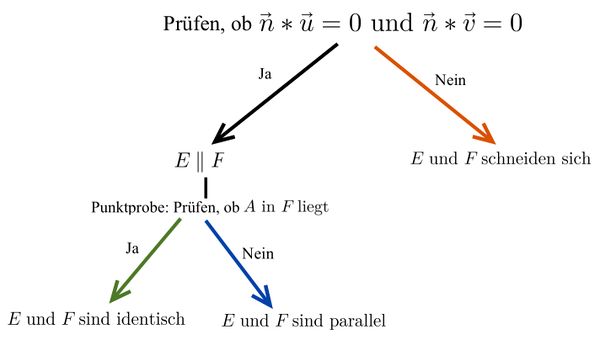
⭐Beide Ebenengleichungen in Koordinatenform
⭐Berechnung des Winkels zwischen Ebene und Ebene