|
|
| Zeile 573: |
Zeile 573: |
| {{Lösung versteckt|1=Die Aussage ist wahr, da all diese Ebenen parallel zur <math>x_3</math>-Achse liegen.|2=Lösung anzeigen|3=Lösung verbergen}} | | {{Lösung versteckt|1=Die Aussage ist wahr, da all diese Ebenen parallel zur <math>x_3</math>-Achse liegen.|2=Lösung anzeigen|3=Lösung verbergen}} |
| | Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }}<br /> | | | Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }}<br /> |
|
| |
| ===⭐Überführung der Parameterform in die Koordinatenform===
| |
|
| |
| <br />{{Box | Beispiel: Von der Parameter- zur Koordinatenform einer Ebenengleichung |
| |
|
| |
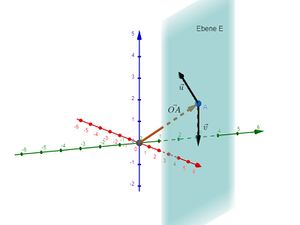
| Wir suchen die Koordinatengleichung der Ebene <math>E: \vec{x} = \begin{pmatrix} 2 \\ 1 \\ 5 \end{pmatrix} + s \cdot \begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix}+ t \cdot \begin{pmatrix} 1 \\ -3 \\ 4 \end{pmatrix}</math>.
| |
|
| |
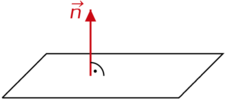
| Ein Normalenvektor <math>\vec{n}</math> muss zu den Spannvektoren <math>\begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix}</math> und <math>\begin{pmatrix} 1 \\ -3 \\ 4 \end{pmatrix}</math> orthogonal (senkrecht) sein, also ist
| |
|
| |
| Hieraus folgt:
| |
|
| |
| <div align="center"><math>\left\vert\begin{alignat}{7}
| |
| n_1 &&\; - \;&& n_2 &&\; + \;&& 0n_3 &&\; = \;&& 0 \\
| |
| n_1 &&\; - \;&& 3n_2 &&\; + \;&& 4n_3 &&\; = \;&& 0\\
| |
| \end{alignat}\right\vert</math></div>
| |
|
| |
| Es gibt auch hier zwei Berechnungsmöglichkeiten - per Hand oder per Taschenrechner. Willst du das Gleichungssystem per Hand lösen kannst du in der ersten Gleichung auf beiden Seite <math>+n_2</math> rechnen und erhält <math>n_1 = n_2</math>. Das Ergebnis für <math>n_1</math> setzt du in die zweite Gleichung ein und berechnest so <math>n_3</math> in Abhängigkeit von <math>n_2</math> und erhälst:
| |
|
| |
| <div align="center"><math>\begin{align}
| |
| & & {-}2n_2 + 4n_3 &= 0 & &\mid +2n_2\\
| |
| \Leftrightarrow & & 4n_3 &= 2n_2 & &\mid :4\\
| |
| \Leftrightarrow & & n_3 &= \tfrac{1}{2} n_2
| |
| \end{align}</math></div>
| |
|
| |
| Durch Einsetzen der berechneten, von n_2 abhängigen Werte in die zweite Gleichung erhalten wir auch n_3 und damit den allgemeinen Normalenvektor in Abhängigkeit von <math>n_2</math>:
| |
|
| |
| <div align="center"><math> \vec{n} = \begin{pmatrix} n_2 \\ n_2 \\ \tfrac{1}{2} n_2 \end{pmatrix} </math></div>
| |
|
| |
| Wählt man z.B. <math>n_2=2</math>, so erhält man <math>n_1=2</math> und <math>n_3=1</math> und damit <math>\vec{n}=\begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix}</math>.
| |
|
| |
| Ansatz für die Koordinatengleichung: <math>E:2x_1+2x_2+x_3=d</math>.
| |
|
| |
| Das <math>d</math> berechnen wir mithilfe des Normalenvektors und dem Ortsvektor des Aufpunktes, d.h. es ist <math>d=\vec{n} \ast \vec{OA}</math>:
| |
|
| |
| <math>2 \cdot 2 + 2 \cdot 1 + 1 \cdot 5=12</math>.
| |
|
| |
| Koordinatengleichung: <math>E:2x_1+2x_2+x_3=12</math>| Hervorhebung1}}
| |
|
| |
| {{Box | ⭐Aufgabe 16: Koordinatengleichung aus Parametergleichung |
| |
| Bestimme eine Koordinatengleichung der Ebene <math>E\colon \vec{x} = \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix} + s \cdot \begin{pmatrix} 1 \\ 3 \\ 0 \end{pmatrix}+ t \cdot \begin{pmatrix} -2 \\ 1 \\ 3 \end{pmatrix}</math>.
| |
|
| |
| {{Lösung versteckt|1=Ein Normalenvektor <math>\vec{n}</math> muss zu den Spannvektoren orthogonal (senkrecht) sein.
| |
|
| |
| Also ist <math>\begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix} \ast \begin{pmatrix} 1 \\ 3 \\ 0 \end{pmatrix}=0</math> und <math>\begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix} \ast \begin{pmatrix} -2 \\ 1 \\ 3 \end{pmatrix}=0</math>.
| |
|
| |
| Hieraus folgt das Gleichungssystem
| |
|
| |
| <div align="center"><math>\left\vert\begin{alignat}{7}
| |
| 1n_1 &&\; + \;&& 3n_2 &&\; + \;&& 0n_3 &&\; = \;&& 0 \\
| |
| {-}2n_1 &&\; + \;&& 1n_2 &&\; + \;&& 3n_3 &&\; = \;&& 0\\
| |
| \end{alignat}\right\vert</math></div>
| |
|
| |
| Es gibt auch hier zwei Berechnungsmöglichkeiten - per Hand oder per Taschenrechner. Wollt ihr das Gleichungssystem per Hand lösen, geht ihr vor wie schon in den vorherigen Aufgaben. Dazu formt ihr die erste Gleichung um und erhaltet:
| |
|
| |
| <div align="center"><math>\begin{align}
| |
| & & 1n_1 + 3n_2 &= 0 & &\mid -3n_2\\
| |
| \Leftrightarrow & & n_1 &= -3n_2
| |
| \end{align}</math></div>
| |
|
| |
| Durch Einsetzen der berechneten, von n_2 abhängigen Werte in die zweite Gleichung erhalten wir auch n_3 und damit den allgemeinen Normalenvektor in Abhängigkeit von <math>n_2</math>:
| |
|
| |
| <div align="center"><math> \vec{n} = \begin{pmatrix} {-}3n_2 \\ n_2 \\ -\tfrac{7}{3} n_2 \end{pmatrix} </math></div>
| |
|
| |
| Für einen speziellen Normalenvektor wählen wir für <math>n_2</math> eine beliebige Zahl aus. Die wählen wir so, dass insgesamt ganzzahlige Zahlen raus kommen. Wenn <math>n_2 = {-}3</math> ist, dann folgt für <math>n_1 = 9</math> und für <math>n_3 = 7</math> .
| |
|
| |
| Daraus folgt für den speziellen Normalenvektor <math> \vec{n} = \begin{pmatrix} 9 \\ -3 \\ 7 \end{pmatrix} </math>
| |
|
| |
| Das <math>d</math> berechnen wir mithilfe des Normalenvektors und dem Ortsvektor des Aufpunktes, d.h. es ist <math>d=\vec{n} \ast \vec{OA}</math>:
| |
|
| |
| <math>9 \cdot 2 - 3 \cdot 1 + 7 \cdot 2=29</math>
| |
|
| |
| Koordinatenform der Ebenengleichung: <math>9x_1 - 3x_2 + 7x_3=29</math>
| |
| |2=mögliche Lösung anzeigen|3=mögliche Lösung verbergen}}
| |
| | Arbeitsmethode | Farbe={{Farbe|orange}} }}
| |
|
| |
| {{Box | ⭐Aufgabe 17: Parameter-, Normalen- und Koordinatengleichung |
| |
| Die Ebene <math>E</math> ist durch die drei Punkte <math>A(7|2|{-}1)</math>, <math>B(4|1|3)</math>, <math>C(1|3|2)</math> festgelegt. Bestimme eine Parametergleichung, eine Normalengleichung und eine Koordinatengleichung der Ebene <math>E</math>.
| |
|
| |
| {{Lösung versteckt|1= Zum Aufstellen einer möglichen Parametergleichung wählen wir beispielsweise den Punkt <math>A</math> als Aufpukt. Die Richtungsvektoren können beispielsweise berechnet werden durch <math>\vec{AB}</math> als ersten Richtungsvektor und <math>\vec{AC}</math> als zweiten. Somit setzt sich die Ebenengleichung wie folgt zusammen:
| |
|
| |
| <math>E\colon \vec{x} = \vec{OA} + s \cdot \vec{AB} + t \cdot \vec{AC}</math>.
| |
|
| |
| Damit ergibt sich:
| |
|
| |
| <math>E\colon \vec{x} = \begin{pmatrix} 7 \\ 2 \\ 1 \end{pmatrix} + s \cdot \begin{pmatrix} -3 \\ -1 \\ 4 \end{pmatrix}+ t \cdot \begin{pmatrix} -6 \\ 1 \\ 3 \end{pmatrix}</math>
| |
| |2=mögliche Lösung (Parameterform) anzeigen|3=mögliche Lösung verbergen}}
| |
|
| |
| {{Lösung versteckt|1=
| |
| Da ein Normalenvektor <math>\vec{n}</math> zu den Spannvektoren orthogonal (senkrecht) sein muss gilt
| |
| <math>\begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix} \ast \begin{pmatrix} -3 \\ -1 \\ 4 \end{pmatrix}=0</math> und <math>\begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix} \ast \begin{pmatrix} -6 \\ 1 \\ 3 \end{pmatrix}=0</math>.
| |
|
| |
| Hieraus folgt das Gleichungssystem
| |
|
| |
| <div align="center"><math>\left\vert\begin{alignat}{7}
| |
| {-}3n_1 &&\; - \;&& 1n_2 &&\; + \;&& 4n_3 &&\; = \;&& 0 \\
| |
| {-}6n_1 &&\; + \;&& 1n_2 &&\; + \;&& 3n_3 &&\; = \;&& 0\\
| |
| \end{alignat}\right\vert</math></div>
| |
|
| |
| Um das Gleichungssystem per Hand zu lösen, behalten wir die erste Gleichung bei und ersetzen die zweite durch die Summe der beiden Gleichungen wodurch wir folgendes Gleichungssystem erhalten:
| |
|
| |
| <div align="center"><math>\left\vert\begin{alignat}{7}
| |
| {-}3n_1 &&\; - \;&& 1n_2 &&\; + \;&& 4n_3 &&\; = \;&& 0 \\
| |
| {-}9n_1 &&\; + \;&& 0n_2 &&\; + \;&& 7n_3 &&\; = \;&& 0\\
| |
| \end{alignat}\right\vert</math></div>
| |
|
| |
| Zur Berechnung eines allgemeinen Normalenvektors formen wir die zweite Gleichung um und erhalten:
| |
|
| |
| <div align="center"><math>\begin{align}
| |
| & & {-}9n_1 + 7n_2 &= 0 & &\mid -7n_2\\
| |
| \Leftrightarrow & & {-}9n_1 &= {-}7n_3 & &\mid :{-}7\\
| |
| \Leftrightarrow & & \tfrac{9}{7}n_1 &= n_3
| |
| \end{align}</math></div>
| |
|
| |
| Durch Einsetzen von <math>n_1</math> und <math>n_3=\tfrac{9}{7}n_1</math> in die erste Gleichung erhalten wir auch <math>n_2</math> als von <math>n_1</math> abhängigen Wert mit <math>n_2=\tfrac{15}{7}</math>. Damit ergibt sich der allgemeine Normalenvektor:
| |
|
| |
| <div align="center"><math> \vec{n} = \begin{pmatrix} n_1 \\ \tfrac{15}{7} n_1 \\ \tfrac{9}{7} n_1 \end{pmatrix} </math></div>
| |
|
| |
| Für einen speziellen Normalenvektor wählen wir für <math>n_1</math> eine beliebige Zahl aus. Die wählen wir so, dass insgesamt ganzzahlige Zahlen raus kommen. Wenn <math>n_1 = {-}7</math> ist, dann folgt für <math>n_2 = {-}15</math> und für <math>n_3 = {-}9</math> .
| |
|
| |
| Daraus folgt für den speziellen Normalenvektor <math> \vec{n} = \begin{pmatrix} -7 \\ -15 \\ -9 \end{pmatrix} </math>.
| |
|
| |
| Außerdem nutzen wir <math>\vec{OA}</math> als Aufpunkt und erhalten somit:
| |
|
| |
| <math>E\colon \vec{x}=\Biggl[\vec{x}-\begin{pmatrix} 7 \\ 2 \\ -1 \end{pmatrix}\Biggr] \cdot \begin{pmatrix} -7 \\ -15 \\ -9 \end{pmatrix}=0</math>
| |
| |2=mögliche Lösung (Normalenform) anzeigen|3=mögliche Lösung verbergen}}
| |
|
| |
| {{Lösung versteckt|1=
| |
| Wir nutzen den eben berechneten Normalenvektor auch zum Aufstellen der Koordinatenform.
| |
|
| |
| Das <math>d</math> berechnen wir mithilfe des Skalarprodukts des Normalenvektors mit dem Orstvektor des Aufpunktes, d.h. es ist <math>d=\vec{n} \ast \vec{OA}</math>:
| |
|
| |
| <math>(-7 \cdot 7) + ((-15) \cdot 2) + ((-9) \cdot (-1)) =-70</math>
| |
|
| |
| Damit ergibt sich folgende Koordinatengleichung:
| |
|
| |
| <math>E:-7x_1-15x_2-9x_3=-70</math>
| |
| |2=mögliche Lösung (Koordinatenform) anzeigen|3=mögliche Lösung verbergen}}
| |
| | Arbeitsmethode}}
| |