Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 436: | Zeile 436: | ||
<div align="center"><math>\left\vert\begin{alignat}{7} | <div align="center"><math>\left\vert\begin{alignat}{7} | ||
{-}3n_1 &&\; | {-}3n_1 &&\; - \;&& 1n_2 &&\; + \;&& 4n_3 &&\; = \;&& 0 \\ | ||
{-}6n_1 &&\; + \;&& 1n_2 &&\; + \;&& 3n_3 &&\; = \;&& 0\\ | {-}6n_1 &&\; + \;&& 1n_2 &&\; + \;&& 3n_3 &&\; = \;&& 0\\ | ||
\end{alignat}\right\vert</math></div> | \end{alignat}\right\vert</math></div> | ||
| Zeile 443: | Zeile 443: | ||
<div align="center"><math>\left\vert\begin{alignat}{7} | <div align="center"><math>\left\vert\begin{alignat}{7} | ||
{-}3n_1 &&\; | {-}3n_1 &&\; - \;&& 1n_2 &&\; + \;&& 4n_3 &&\; = \;&& 0 \\ | ||
{-}9n_1 &&\; + \;&& 0n_2 &&\; + \;&& 7n_3 &&\; = \;&& 0\\ | {-}9n_1 &&\; + \;&& 0n_2 &&\; + \;&& 7n_3 &&\; = \;&& 0\\ | ||
\end{alignat}\right\vert</math></div> | \end{alignat}\right\vert</math></div> | ||
| Zeile 457: | Zeile 457: | ||
Durch Einsetzen von <math>n_1</math> und <math>n_3=\tfrac{9}{7}n_1</math> in die erste Gleichung erhalten wir auch <math>n_2</math> als von <math>n_1</math> abhängigen Wert mit <math>n_2=\tfrac{15}{7}</math>. Damit ergibt sich der allgemeine Normalenvektor: | Durch Einsetzen von <math>n_1</math> und <math>n_3=\tfrac{9}{7}n_1</math> in die erste Gleichung erhalten wir auch <math>n_2</math> als von <math>n_1</math> abhängigen Wert mit <math>n_2=\tfrac{15}{7}</math>. Damit ergibt sich der allgemeine Normalenvektor: | ||
<div align="center"><math> \vec{n} = \begin{pmatrix} n_1 \\ \tfrac{15}{7} n_1 \\ | <div align="center"><math> \vec{n} = \begin{pmatrix} n_1 \\ \tfrac{15}{7} n_1 \\ \tfrac{9}{7} n_1 \end{pmatrix} </math></div> | ||
Für einen speziellen Normalenvektor wählen wir für <math>n_1</math> eine beliebige Zahl aus. Die wählen wir so, dass insgesamt ganzzahlige Zahlen raus kommen. Wenn <math>n_1 = {-}7</math> ist, dann folgt für <math>n_2 = {-}15</math> und für <math>n_3 = {-}9</math> . | Für einen speziellen Normalenvektor wählen wir für <math>n_1</math> eine beliebige Zahl aus. Die wählen wir so, dass insgesamt ganzzahlige Zahlen raus kommen. Wenn <math>n_1 = {-}7</math> ist, dann folgt für <math>n_2 = {-}15</math> und für <math>n_3 = {-}9</math> . | ||
Version vom 6. Juni 2021, 22:01 Uhr
Die Parameterform und die Punktprobe
Die Punktprobe
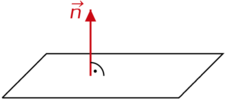
⭐ Normalenvektor
⭐ Normalenform und Koordinatenform von Ebenengleichungen
⭐Überführung der Parameterform in die Koordinatenform