Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung |
Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 414: | Zeile 414: | ||
'''b)''' Begründe: Unterscheiden sich die Koordinatengleichungen der Form <math>E\colon ax_1+bx_2+cx_3=d</math> von zwei Ebenen nur in der Konstanten <math>d</math>, dann sind die Ebenen zueinander parallel. | '''b)''' Begründe: Unterscheiden sich die Koordinatengleichungen der Form <math>E\colon ax_1+bx_2+cx_3=d</math> von zwei Ebenen nur in der Konstanten <math>d</math>, dann sind die Ebenen zueinander parallel. | ||
{{Lösung versteckt|1=Wenn sich die beiden Ebenengleichungen nur in <math>d</math> unterscheiden, ist der Vektor <math>\begin{pmatrix} a \\ b \\ c \end{pmatrix} | {{Lösung versteckt|1=Wenn sich die beiden Ebenengleichungen nur in <math>d</math> unterscheiden, ist der Vektor <math>\begin{pmatrix} a \\ b \\ c \end{pmatrix}</math> ein Normalenvektor von beiden Ebenen, das heißt er liegt orthogonal zu beiden Ebenen. Damit müssen die Ebenen parallel sein.|2=Lösung anzeigen|3=Lösung verbergen}} | ||
'''c)''' Beurteile: Alle Ebenen, bei denen in der Koordinatengleichung <math>E\colon ax_1+bx_2+cx_3=d</math> die Koeffizienten <math>a</math> und <math>b</math> ungleich Null, aber <math>c=0</math> ist, haben eine Gemeinsamkeit bezüglich ihrer Lage. | '''c)''' Beurteile: Alle Ebenen, bei denen in der Koordinatengleichung <math>E\colon ax_1+bx_2+cx_3=d</math> die Koeffizienten <math>a</math> und <math>b</math> ungleich Null, aber <math>c=0</math> ist, haben eine Gemeinsamkeit bezüglich ihrer Lage. | ||
| Zeile 460: | Zeile 460: | ||
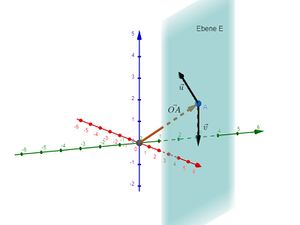
Normalenvektor: <math>\begin{pmatrix} 9 \\ -3 \\ 7 \end{pmatrix}</math>. | Normalenvektor: <math>\begin{pmatrix} 9 \\ -3 \\ 7 \end{pmatrix}</math>. | ||
Das <math>d</math> berechnen wir mithilfe des Normalenvektors und | Das <math>d</math> berechnen wir mithilfe des Normalenvektors und dem Orstvektor des Aufpunktes, d.h. es ist <math>d=\vec{n} \ast \vec{OA}</math>: | ||
<math>9 \cdot 2 - 3 \cdot 1 + 7 \cdot 2=29</math> | <math>9 \cdot 2 - 3 \cdot 1 + 7 \cdot 2=29</math> | ||
Version vom 3. Juni 2021, 13:12 Uhr
Die Parameterform und die Punktprobe
Die Punktprobe
Spurpunkte
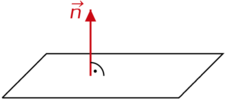
⭐ Normalenvektor
⭐ Normalenform und Koordinatenform von Ebenengleichungen
⭐Überführung der Parameterform in die Koordinatenform