Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 90: | Zeile 90: | ||
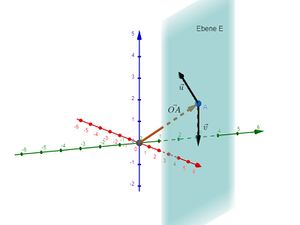
Liegt der Punkt <math>A({-}1|1|{-}1)</math> in der Ebene <math>E:\vec{x}=\begin{pmatrix} 1 \\ 2 \\ 0 \end{pmatrix}+s \cdot \begin{pmatrix} {-}2 \\ 0 \\ 3 \end{pmatrix} +t\cdot \begin{pmatrix} 0 \\ 1 \\ 4 \end{pmatrix} </math>? | Liegt der Punkt <math>A({-}1|1|{-}1)</math> in der Ebene <math>E:\vec{x}=\begin{pmatrix} 1 \\ 2 \\ 0 \end{pmatrix}+s \cdot \begin{pmatrix} {-}2 \\ 0 \\ 3 \end{pmatrix} +t\cdot \begin{pmatrix} 0 \\ 1 \\ 4 \end{pmatrix} </math>? | ||
Wenn ja, dann müsste der zu <math>A</math> gehörende Ortsvektor <math>\vec{OA} = \begin{pmatrix} {-}1 \\ 1 \\ {-}1 \end{pmatrix}</math> die Ebenengleichung erfüllen, d.h. es müsste ein Paar reeller Zahlen <math> | Wenn ja, dann müsste der zu <math>A</math> gehörende Ortsvektor <math>\vec{OA} = \begin{pmatrix} {-}1 \\ 1 \\ {-}1 \end{pmatrix}</math> die Ebenengleichung erfüllen, d.h. es müsste ein Paar reeller Zahlen <math>s,t</math> geben, für die gilt: | ||
<div align="center"><math>\vec{OA}=\vec{p}+ | <div align="center"><math>\vec{OA}=\vec{p}+s \cdot \vec{u}+t \cdot \vec{v}</math></div> | ||
| Zeile 100: | Zeile 100: | ||
<div align="center"><math>\begin{array}{crcrcr}\\ | <div align="center"><math>\begin{array}{crcrcr}\\ | ||
\text{I}\quad & {-} | \text{I}\quad & {-}2s & + & 0t & = & {-}2\\ | ||
\text{II}\quad & | \text{II}\quad & 0s & + & 1t & = & {-}1\\ | ||
\text{III}\quad & | \text{III}\quad & 3s & + & 4t & = & {-}1 | ||
\end{array}</math></div> | \end{array}</math></div> | ||
Aus der ersten Gleichung folgt <math> | <div align="center"><math>\left\vert\begin{alignat}{7} | ||
1 &&\; + \;&& {-}2s &&\; + \;&& 0t &&\; = \;&& {-}1 \\ | |||
2 &&\; + \;&& 0s &&\; + \;&& 1t &&\; = \;&& 1\\ | |||
0 &&\; + \;&& 3s &&\; + \;&& 4t &&\; = \;&& {-}1 | |||
\end{alignat}\right\vert</math></div> | |||
Aus der ersten Gleichung folgt <math>s=1</math>, die zweite Gleichung ergibt <math>t={-}1</math>. | |||
Die dritte Gleichung ist für diese Werte ebenfalls erfüllt, das heißt der Punkt <math>A</math> liegt in der Ebene <math>E</math>.| 3=Hervorhebung1}} | Die dritte Gleichung ist für diese Werte ebenfalls erfüllt, das heißt der Punkt <math>A</math> liegt in der Ebene <math>E</math>.| 3=Hervorhebung1}} | ||
Version vom 2. Juni 2021, 10:52 Uhr
Die Parameterform und die Punktprobe
Die Punktprobe
Spurpunkte
⭐ Normalenvektor
⭐ Normalenform und Koordinatenform von Ebenengleichungen
⭐Überführung der Parameterform in die Koordinatenform