Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 117: | Zeile 117: | ||
|Arbeitsmethode | Farbe={{Farbe|orange}}}} | |Arbeitsmethode | Farbe={{Farbe|orange}}}} | ||
{{Box | Aufgabe | {{Box | Aufgabe 4: Schatten eines Sonnensegels | | ||
Da es Frau Meier im Sommer auf ihrer Terrasse gerne schattig haben möchte, spannt sie ein dreieckiges Segeltuch auf. Die Eckpunkte des Segeltuchs sind <math>A (9|{-}5|7), B (6|{-}5|7)</math> und <math>C (7|{-}10|11)</math>. Die Terrasse wird modelliert durch die Ebene <math>E: \vec{x}= \left( \begin{matrix} {-}13\\ {-}7\\ 0 \end{matrix} \right) + r \cdot \left( \begin{matrix} 1\\ 0\\ 0 \end{matrix} \right)+ s \cdot \left( \begin{matrix} 0\\ 1\\ 0 \end{matrix} \right) </math>. Die Richtung der Sonnenstrahlen entspricht dem Vektor <math>\vec{s} = \left( \begin{matrix} -2\\ {-}2\\ {-}10 \end{matrix} \right)</math>. In welchem Bereich hat Frau Meier nun Schatten? | Da es Frau Meier im Sommer auf ihrer Terrasse gerne schattig haben möchte, spannt sie ein dreieckiges Segeltuch auf. Die Eckpunkte des Segeltuchs sind <math>A (9|{-}5|7), B (6|{-}5|7)</math> und <math>C (7|{-}10|11)</math>. Die Terrasse wird modelliert durch die Ebene <math>E: \vec{x}= \left( \begin{matrix} {-}13\\ {-}7\\ 0 \end{matrix} \right) + r \cdot \left( \begin{matrix} 1\\ 0\\ 0 \end{matrix} \right)+ s \cdot \left( \begin{matrix} 0\\ 1\\ 0 \end{matrix} \right) </math>. Die Richtung der Sonnenstrahlen entspricht dem Vektor <math>\vec{s} = \left( \begin{matrix} -2\\ {-}2\\ {-}10 \end{matrix} \right)</math>. In welchem Bereich hat Frau Meier nun Schatten? | ||
| Zeile 205: | Zeile 205: | ||
{{Box |⭐ Aufgabe : Untersuchung der Lagebeziehung einer Gerade und einer Ebene in Koordinatenform | | {{Box |⭐ Aufgabe 5: Untersuchung der Lagebeziehung einer Gerade und einer Ebene in Koordinatenform | | ||
a) Gegeben sind eine Ebene <math>E\colon 2x_1 + x_2 - x_3 = 5 </math> und eine Gerade <math>g\colon \vec{x}=\left( \begin{matrix} 3\\ 0\\ 2 \end{matrix} \right) + r \cdot \left( \begin{matrix} -3\\ 5\\ {-}1 \end{matrix} \right) </math>. Bestimme die Lagebeziehung von Gerade und Ebene. | a) Gegeben sind eine Ebene <math>E\colon 2x_1 + x_2 - x_3 = 5 </math> und eine Gerade <math>g\colon \vec{x}=\left( \begin{matrix} 3\\ 0\\ 2 \end{matrix} \right) + r \cdot \left( \begin{matrix} -3\\ 5\\ {-}1 \end{matrix} \right) </math>. Bestimme die Lagebeziehung von Gerade und Ebene. | ||
| Zeile 269: | Zeile 269: | ||
| Arbeitsmethode | Farbe={{Farbe|orange}}}} | | Arbeitsmethode | Farbe={{Farbe|orange}}}} | ||
{{Box|⭐ Aufgabe | {{Box|⭐ Aufgabe 6: Bestimme den Parameter | | ||
Gegeben ist eine Ebene <math>E\colon -2x_1 + 3x_2 - x_3 = 3</math>. | Gegeben ist eine Ebene <math>E\colon -2x_1 + 3x_2 - x_3 = 3</math>. | ||
Bestimme <math>l</math> und <math>m</math> in den folgenden Geraden so, dass die jeweils angegebene Lagebeziehung erfüllt ist. | Bestimme <math>l</math> und <math>m</math> in den folgenden Geraden so, dass die jeweils angegebene Lagebeziehung erfüllt ist. | ||
| Zeile 297: | Zeile 297: | ||
|Arbeitsmethode}} | |Arbeitsmethode}} | ||
{{Box|⭐ Aufgabe | {{Box|⭐ Aufgabe 7: Flugzeug | | ||
Ein Flugzeug startet am Flughafen Münster-Osnabrück. Seine Flugbahn in den ersten 6 Minuten nach dem Start wird durch die Gerade <math>j\colon \vec{x} = \left( \begin{matrix} 10\\ 23 \\0 \end{matrix} \right) + t \cdot \left( \begin{matrix} -2\\ {-}5\\ \frac{1}{2} \end{matrix} \right)</math> beschrieben, wobei <math> t</math> die Zeit in Minuten nach dem Start bezeichnet. Die Ebene <math> E: 2x_1+x_2=-2 </math> beschreibt eine Nebelwand. | Ein Flugzeug startet am Flughafen Münster-Osnabrück. Seine Flugbahn in den ersten 6 Minuten nach dem Start wird durch die Gerade <math>j\colon \vec{x} = \left( \begin{matrix} 10\\ 23 \\0 \end{matrix} \right) + t \cdot \left( \begin{matrix} -2\\ {-}5\\ \frac{1}{2} \end{matrix} \right)</math> beschrieben, wobei <math> t</math> die Zeit in Minuten nach dem Start bezeichnet. Die Ebene <math> E: 2x_1+x_2=-2 </math> beschreibt eine Nebelwand. | ||
| Zeile 345: | Zeile 345: | ||
| Merksatz}} | | Merksatz}} | ||
{{Box | Aufgabe ⭐: Berechnung des Winkels zwischen Gerade und Ebene | | {{Box | Aufgabe 8 ⭐: Berechnung des Winkels zwischen Gerade und Ebene | | ||
Gegeben sind die Gerade <math>g\colon \vec{x}=\left( \begin{matrix} {-}1\\ 3\\ 6 \end{matrix} \right) + r \cdot \left( \begin{matrix} 8\\ 2\\ 0 \end{matrix} \right) </math> und die Ebene <math>E\colon 2x_1 + x_2 + 4 x_3 = {-}27</math>. Bestimme den Winkel, unter dem sich die Gerade <math>g</math> und die Ebene <math>E</math> schneiden. | Gegeben sind die Gerade <math>g\colon \vec{x}=\left( \begin{matrix} {-}1\\ 3\\ 6 \end{matrix} \right) + r \cdot \left( \begin{matrix} 8\\ 2\\ 0 \end{matrix} \right) </math> und die Ebene <math>E\colon 2x_1 + x_2 + 4 x_3 = {-}27</math>. Bestimme den Winkel, unter dem sich die Gerade <math>g</math> und die Ebene <math>E</math> schneiden. | ||
| Zeile 367: | Zeile 367: | ||
| Arbeitsmethode | Farbe={{Farbe|orange}} }} | | Arbeitsmethode | Farbe={{Farbe|orange}} }} | ||
{{Box | Aufgabe | {{Box | Aufgabe 9⭐: Trinkpäckchen | | ||
[[Datei:Trinkpäckchen einfach.jpg|mini|Trinkpäckchen]] | [[Datei:Trinkpäckchen einfach.jpg|mini|Trinkpäckchen]] | ||
| Zeile 397: | Zeile 397: | ||
{{Box | Aufgabe | {{Box | Aufgabe 10⭐: Gerade gesucht | | ||
Bisher wurde mit der Formel zur Winkelberechnung nur der Winkel berechnet. Die Formel kann jedoch auch genutzt werden, um bei einem vorgegebenen Winkel die Lage der Gerade oder Ebene zu bestimmen. | Bisher wurde mit der Formel zur Winkelberechnung nur der Winkel berechnet. Die Formel kann jedoch auch genutzt werden, um bei einem vorgegebenen Winkel die Lage der Gerade oder Ebene zu bestimmen. | ||
Version vom 25. Mai 2021, 14:49 Uhr
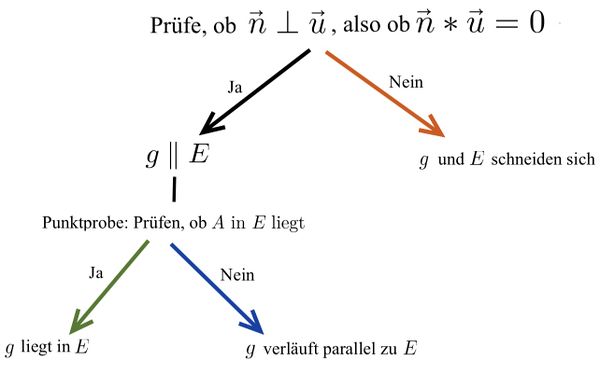
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
Untersuchung der Lagebeziehung zwischen Gerade und Ebene
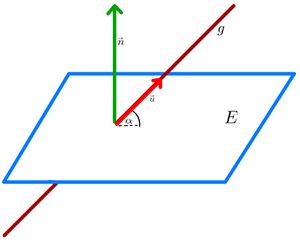
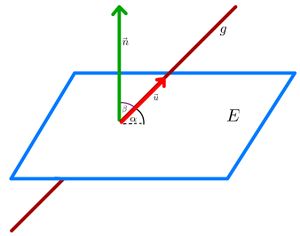
⭐Berechnung des Winkels zwischen Gerade und Ebene
Lagebeziehung Ebene-Ebene
Mögliche Lagebeziehungen zwischen zwei Ebenen
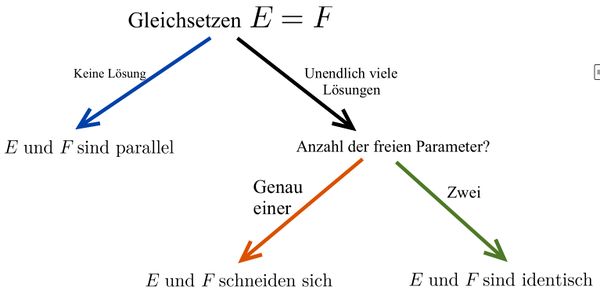
Untersuchung der Lagebeziehung von zwei Ebenen
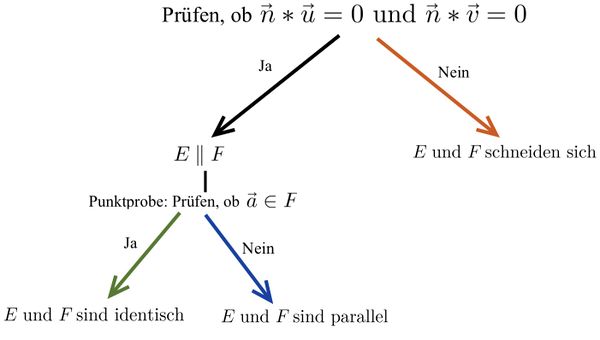
Beide Ebenengleichungen in Parameterform
⭐Ebenengleichungen in Parameter- und Koordinatenform
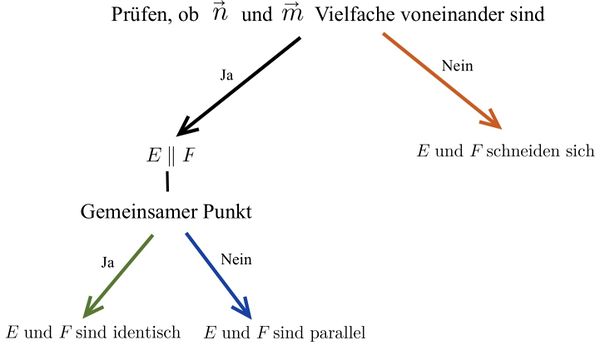
⭐Beide Ebenengleichungen in Koordinatenform
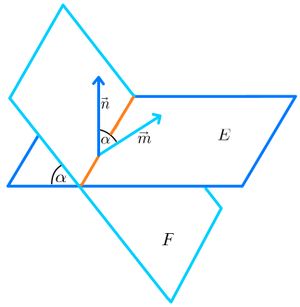
⭐Berechnung des Winkels zwischen Ebene und Ebene