Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 332: | Zeile 332: | ||
<div align="center"><math>\begin{array}{crcrcrcr}\\ | <div align="center"><math>\begin{array}{crcrcrcr}\\ | ||
\text{I}\quad & 28n_1 & + & 24n_2 | \text{I}\quad & 28n_1 & + & 24n_2 & = & 0\\ | ||
\text{II}\quad & {-}21n_1 & + & 10n_2 & + & 0,5n_3 & = & 0 | \text{II}\quad & {-}21n_1 & + & 10n_2 & + & 0,5n_3 & = & 0 | ||
| Zeile 348: | Zeile 348: | ||
'''c)''' Berechne die Zahl z derart, dass R in der Ebene liegt. | '''c)''' Berechne die Zahl z derart, dass R in der Ebene liegt. | ||
{{Lösung versteckt|1=<math>6 \cdot (-30) - 7 \cdot 20 + 392z=0</math> | {{Lösung versteckt|1=<math>6 \cdot (-30) - 7 \cdot 20 + 392z=0</math> | ||
| Zeile 361: | Zeile 360: | ||
.|2=mögliche Lösung anzeigen|3=mögliche Lösung verbergen}} | .|2=mögliche Lösung anzeigen|3=mögliche Lösung verbergen}} | ||
| Arbeitsmethode}} | |||
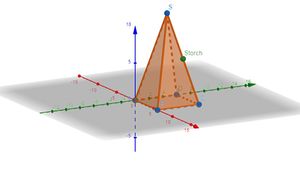
{{Box | ⭐Aufgabe 14: Schattenwurf (Gerade und Ebene in Koordinatenform) |Ein Baum mit dem Fußpunkt <math>F({-}2|1|0)</math> und der Spitze <math>S({-}2|1|15)</math> wird von der Sonne bestrahlt, deren Sonnenstrahlen parallel zum Vektor <math>\begin{pmatrix} 4 \\ 5 \\ 7 \end{pmatrix}</math> verlaufen. Der Baum wirft einen Schatten auf einen Hang, der durch die Ebene <math>E\colon x_1+2x_2+x_3={-}6</math> beschrieben wird. | {{Box | ⭐Aufgabe 14: Schattenwurf (Gerade und Ebene in Koordinatenform) |Ein Baum mit dem Fußpunkt <math>F({-}2|1|0)</math> und der Spitze <math>S({-}2|1|15)</math> wird von der Sonne bestrahlt, deren Sonnenstrahlen parallel zum Vektor <math>\begin{pmatrix} 4 \\ 5 \\ 7 \end{pmatrix}</math> verlaufen. Der Baum wirft einen Schatten auf einen Hang, der durch die Ebene <math>E\colon x_1+2x_2+x_3={-}6</math> beschrieben wird. | ||
Version vom 9. Mai 2021, 20:57 Uhr
Die Parameterform und die Punktprobe
Die Punktprobe
Spurpunkte
⭐ Normalenvektor
⭐ Normalenform und Koordinatenform von Ebenengleichungen
Der Schattenpunkt T entspricht dem Schnitt der Ebene E mit der Geraden, die durch S verläuft und den Richtungsvektor der Sonnenstrahlen besitzt.
Geradengleichung:
Einsetzen der Zeilen der Geradengleichung in die Ebenengleichung:
Durch Umformen und Ausmultiplizieren erhält man:
Einsetzen von in die Geradengleichung ergibt den Schnittpunkt .
Schattenlänge des Baumes: LE.
Die Aussage ist wahr, da all diese Ebenen parallel zur -Achse liegen.
⭐Überführung der Parameterform in die Koordinatenform
Ein Normalenvektor muss zu den Spannvektoren orthogonal (senkrecht) sein.
Also ist und .
Hieraus folgt das Gleichungssystem
.
Wählt man z.B. folgt durch Einsetzen in das Gleichungssystem und Umformen: und .
Normalenvektor: .
Das berechnen wir durch :
Koordinatenform der Ebenengleichung: