Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Marie (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 190: | Zeile 190: | ||
{{Box|⭐ Aufgabe 5: Beamer | | {{Box|⭐ Aufgabe 5: Beamer | | ||
Luca hält einen Vortrag vor seiner Klasse. Mit einem Laserpointer möchte er auf einer Karte an der Wand etwas zeigen. Die Wand des Klassenraums wird durch die Ebene <math>E\colon x_2 + 3x_3 = 2</math> dargestellt. Der Strahl des Laserpointers wird durch die Gerade <math>j\colon \vec{x} = \left( \begin{matrix} {-}5\\ 1 \frac{3}{2} \end{matrix} \right) + s \cdot \left( \begin{matrix} 1\\ 2\\ \frac{1}{2} \end{matrix} \right)</math> modelliert. | Luca hält einen Vortrag vor seiner Klasse. Mit einem Laserpointer möchte er auf einer Karte an der Wand etwas zeigen. Die Wand des Klassenraums wird durch die Ebene <math>E\colon x_2 + 3x_3 = 2</math> dargestellt. Der Strahl des Laserpointers wird durch die Gerade <math>j\colon \vec{x} = \left( \begin{matrix} {-}5\\ 1 \\ \frac{3}{2} \end{matrix} \right) + s \cdot \left( \begin{matrix} 1\\ 2\\ \frac{1}{2} \end{matrix} \right)</math> modelliert. | ||
Berechne ohne Taschenrechner, wo der Strahl aus Lucas Laserpointer auf die Karte an der Wand trifft. | Berechne ohne Taschenrechner, wo der Strahl aus Lucas Laserpointer auf die Karte an der Wand trifft. | ||
{{Lösung versteckt|1= Berechne den Schnittpunkt der Gerade mit der Ebene, indem du die einzelnen Koordinaten der Gerade in die Ebenengleichung einsetzt.|2=Tipp anzeigen|3=Tipp verbergen}} | {{Lösung versteckt|1= Berechne den Schnittpunkt der Gerade mit der Ebene, indem du die einzelnen Koordinaten der Gerade in die Ebenengleichung einsetzt.|2=Tipp anzeigen|3=Tipp verbergen}} | ||
Version vom 10. Mai 2021, 07:20 Uhr
Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".
In diesem Lernpfadkapitel geht es um die Lagebeziehung zwischen einer Gerade und einer Ebene oder zwischen zwei Ebenen inklusive der Berechnung der Schnittwinkel.
Bei den Aufgaben unterscheiden wir folgende Typen:
- In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
- Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit.
- Und Aufgaben mit grünem Streifen sind Knobelaufgaben.
- Aufgaben und Kapitel, die mit einem ⭐ gekennzeichnet sind, sind nur für den LK gedacht.
Das Lernpfadkapitel ist so aufgebaut, dass ihr in jedem Abschnitt zuerst grundlegende Inhalte mithilfe der Merkkästen wiederholen könnt. Anschließend findet ihr eine Beispielaufgabe, in der die Inhalte veranschaulicht werden. Am Ende jedes Abschnittes gibt es Übungsaufgaben mit Tipps und Lösungen, sodass ihr üben und euch selbst überprüfen könnt.
Inhaltsverzeichnis
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
Untersuchung der Lagebeziehung zwischen Gerade und Ebene
Gegeben sind eine Ebene und eine Gerade
. Untersuche die Lagebeziehung der Gerade und der Ebene und bestimme gegebenenfalls den Schnittpunkt.
1. Schritt: Setze die Geraden- und Ebenengleichung gleich:
2. Schritt: Stelle das zugehörige lineare Gleichungssystem auf:
3. Schritt: Löse das Gleichungssystem mit dem Gaußverfahren oder dem Taschenrechner:
4. Schritt: Interpretiere die Lösung des Gleichungssystems anhand der Anzahl der Lösungen. Da das Gleichungssystem nur eine Lösung hat, besitzen die Ebene und die Gerade
nur einen gemeinsamen Punkt. Also schneidet die Gerade die Ebene.
5. Schritt: Da sich die Ebene und die Gerade
schneiden, kannst du den Schnittpunkt der beiden berechnen. Setze dafür den Parameter
in die Geradengleichung ein:
Alternativ kannst du die Parameter und
in die Ebenengleichung einsetzen und erhältst den gleichen Punkt.
Gegeben ist eine Ebene . Untersuche die Lagebeziehung zwischen dieser Ebene und den untenstehenden Geraden. Ziehe die Geraden in das entsprechende Feld.
1. Setze die Geradengleichung mit der Ebenengleichung gleich.
2. Stelle ein LGS auf.
3. Löse das LGS mit dem Gaußverfahren oder dem Taschenrechner.
4. Die Anzahl der Lösungen zeigt dir, wie viele gemeinsamen Punkte die Gerade und die Ebene haben. Daran kannst du die Lagebeziehung erkennen.
Da es Frau Meier im Sommer auf ihrer Terrasse gerne schattig haben möchte, spannt sie ein dreieckiges Segeltuch auf. Die Eckpunkte des Segeltuchs sind und
. Die Terrasse wird modelliert durch die
-Ebene. Die Sonne scheint aus Richtung
. In welchem Bereich hat Frau Meier nun Schatten?
1. Schritt: Stelle die Geradengleichungen durch die Eckpunkte des Sonnensegels in Richtung der Sonnenstrahlen auf: ,
,
2. Schritt: Berechne die Schnittpunkte der Geraden mit der -Ebene. Da du weißt, dass jeder Punkt in dieser Ebene von der Form
ist, kannst du diesen Punkt mit der Geradengleichung gleichsetzen.
Berechnung von :
.
Berechnung von :
.
Berechnung von :
.
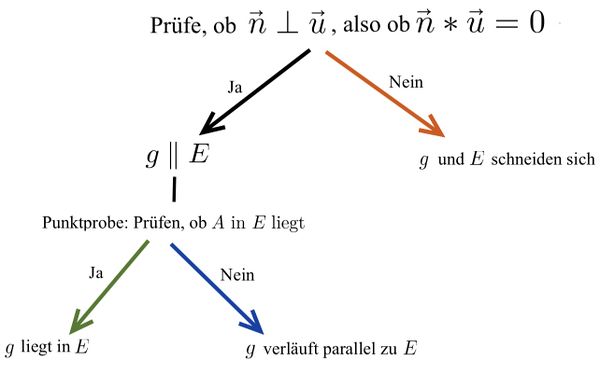
Bei der Bestimmung der Lagebeziehung zwischen einer Gerade und einer Ebene
kann dir der Normalenvektor der Ebene helfen.
Wenn der Richtungsvektor der Gerade und der Normalenvektor der Ebene orthogonal zueinander sind und Gerade und Ebene keinen gemeinsamen Punkt besitzen, so sind sie parallel zueinander.
Wenn der Richtungsvektor der Gerade und der Normalenvektor der Ebene orthogonal zueinander sind und Gerade und Ebene unendlich viele gemeinsame Punkte besitzen, so liegt die Gerade in der Ebene.
Wenn der Richtungsvektor der Gerade und der Normalenvektor der Ebene nicht orthogonal zueinander sind, dann schneiden sich die Gerade und die Ebene und es kann ein Schnittpunkt bestimmt werden.
Gegeben sind eine Ebene und eine Gerade
. Bestimme die Lagebeziehung von Gerade und Ebene.
1. Schritt: Prüfe, ob der Richtungsvektor der Gerade orthogonal zum Normalenvektor der Ebene liegt:
2. Schritt: Prüfe durch eine Punktprobe, ob der Stützvektor der Gerade in der Ebene liegt:
Der Stützvektor liegt nicht in der Ebene. Daher verlaufen die Gerade
und die Ebene
parallel zueinander.
Gegeben ist eine Ebene .
Bestimme
und
in den folgenden Geraden so, dass die entsprechende Lagebeziehung erfüllt ist.
a) Die Gerade soll parallel zur Ebene
verlaufen.
.
b) Die Gerade soll in der Ebene
liegen.
Finde zuerst m: .
Damit die beiden Vektoren orthogonal zueinander sind, muss das Skalarprodukt
sein:
.
c) Die Gerade soll die Ebene
schneiden.
Luca hält einen Vortrag vor seiner Klasse. Mit einem Laserpointer möchte er auf einer Karte an der Wand etwas zeigen. Die Wand des Klassenraums wird durch die Ebene dargestellt. Der Strahl des Laserpointers wird durch die Gerade
modelliert.
Berechne ohne Taschenrechner, wo der Strahl aus Lucas Laserpointer auf die Karte an der Wand trifft.
Setze die einzelnen Koordinaten der Gerade in die Ebenengleichung ein:
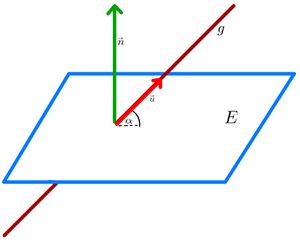
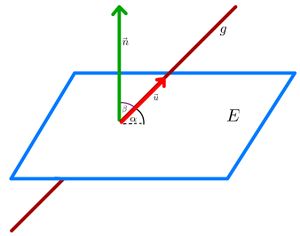
⭐Berechnung des Winkels zwischen Gerade und Ebene
Sei eine Ebene mit dem Normalenvektor
und
eine Gerade mit dem Richtungsvektor
. Der Schnittwinkel
zwischen
und
kann mit folgender Formel berechnet werden:
.
Ist nach dem Schnittwinkel gefragt, so ist immer der kleinere der beiden Winkel gesucht, die von Gerade und Ebene eingeschlossen werden. Dein berechneter Winkel darf also nur zwischen
und
liegen. Ist dein berechneter Winkel
, so musst du
berechnen, und erhälst so den kleineren der beiden Winkel. In einigen Textaufgaben ist jedoch der größere der beiden Winkel gesucht. Hier können dir Skizzen helfen.
Wenn du wissen möchtest, warum du nicht - wie beim Winkel zwischen zwei Geraden - den Kosinus benutzt, kannst du das hier nachlesen:
Der Normalenvektor einer Ebene steht in einem
Winkel zur Ebene
.
Gegeben sind die Gerade und die Ebene
. Bestimme den Winkel, unter dem sich die Gerade
und die Ebene
schneiden.
1. Schritt: Notiere den Richtungvektor der Gerade und den Normalenvektor
der Ebene.
und
2. Schritt: Setze die Vektoren in die Formel ein.
3. Schritt: Forme die Gleichung um.
Der Winkel beträgt also .
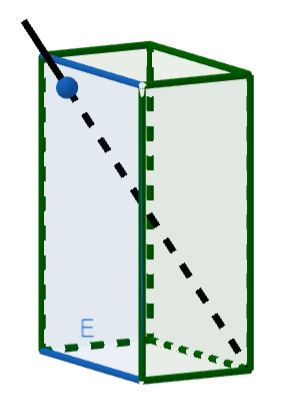
Eine Schulklasse nimmt auf ihrem Wandertag viele Trinkpäckchen mit. Einige Kinder ärgern sich, dass sie mit dem Strohhalm nicht gut in die letzte Ecke kommen. Berechne den Winkel, in dem die Kinder den Strohhalm halten müssen, um auch an den Saft in der letzten Ecke zu kommen.
Jedes Trinkpäckchen hat die Form eines Quaders (siehe Abbildung). Die Seite, auf der sich das Loch für den Strohhalm befindet, kann durch die Ebene beschrieben werden.
Wenn der Strohhalm so in das Trinkpäckchen gesteckt wird, das er in der hintersten Ecke anstößt, kann er durch die Gerade veranschaulicht werden:
.
Gesucht wird der Winkel zwischen der Gerade und der Ebene
. Der Richtungsvektor der Gerade ist
. Der Normalenvektor der Ebene kann abgelesen werden:
.
Einsetzen der Vektoren in die Formel liefert:
Mithilfe des Taschenrechners kann das Ergebnis berechnet werden:
Eine Gerade soll die
-
-Ebene in einem Winkel von
schneiden. Über die Gerade
ist nur bekannt, dass sie im Punkt
beginnt und sie in Richtung des Vektors
verläuft. Stelle die Gerade
auf.
Bisher wurde mit der Formel zur Winkelberechnung nur der Winkel berechnet. Die Formel kann jedoch auch genutzt werden, um bei einem vorgegebenen Winkel die Lage der Gerade oder Ebene zu bestimmen.
Bestimme dafür zuerst den Normalenvektor der Ebene. Da es sich um die -
-Ebene handelt, lautet der Normalenvektor
.
Nun können der Normalenvektor der Ebene, der Richtungsvektor der Gerade und der vorgegebene Winkel in die Formel eingesetzt werden:
Löst man die Gleichung mithilfe des Taschenrechners, erhält man das Ergebnis: .
Lagebeziehung Ebene-Ebene
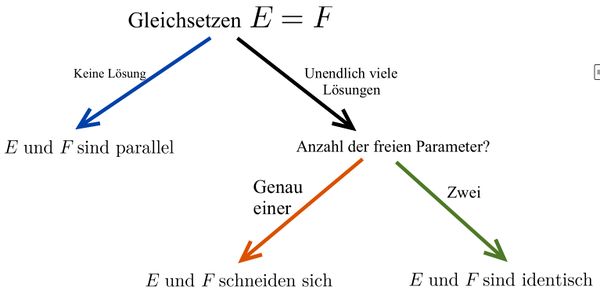
Mögliche Lagebeziehungen zwischen zwei Ebenen
Untersuchung der Lagebeziehung von zwei Ebenen
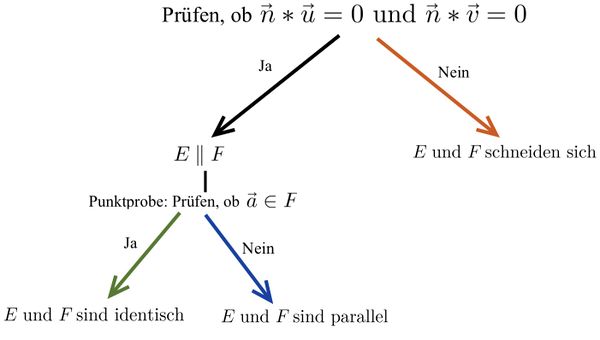
Beide Ebenengleichungen in Parameterform
Gegeben sind eine Ebene und eine Ebene
.
Untersuche die Lagebeziehung der beiden Ebenen.
1. Schritt: Setze die beiden Ebenengleichungen gleich.
2. Schritt: Stelle das zugehörige lineare Gleichungssystem auf.
3. Schritt: Löse das Gleichungssystem mit dem Gaußverfahren oder dem Taschenrechner:
4. Schritt: Interpretiere die Lösung des Gleichungssystems:
In der dritten Zeile der Lösungsmatrix befindet sich ein Widerspruch. Somit hat das LGS keine Lösung und die beiden Ebenen sind parallel.
Interpretiere die jeweilige Situation geometrisch.
a)
b)
c)
⭐Ebenengleichungen in Parameter- und Koordinatenform
Gegeben sind eine Ebene und eine Ebene
.
Untersuche die Lagebeziehung der beiden Ebenen.
1. Schritt: Prüfe, ob die Richtungsvektoren und
der Ebene
orthogonal zum Normalenvektor
der Ebene
liegen.
Hierfür muss gelten, dass und
.
2.Schritt: Interpretiere die Lösung des Skalarproduktes:
Da das Skalarprodukt der Vektoren ist, liegen sie orthogonal zueinander. Das bedeutet, dass die Ebenen sich nicht in einer Schnittgeraden schneiden, sondern entweder identisch oder parallel sind.
3. Schritt: Überprüfe die Lagebeziehung mithilfe der Punktprobe.
Setze hierfür den Stützvektor (Aufpunkt) der Ebene in die Ebenengleichung der Ebene
ein.
4. Schritt: Interpretiere die Lösung der Punktprobe.
Da der Aufpunkt die Koordinatengleichung von erfüllt, liegt
in
und die Ebenen sind identisch.
Untersuche die Lagebeziehung der jeweiligen Ebenen.
a)
Prüfe, ob die Richtungsvektoren und
der Ebene
orthogonal zum Normalenvektor
der Ebene
liegen.
b)
Prüfe, ob die Richtungsvektoren und
der Ebene
orthogonal zum Normalenvektor
der Ebene
liegen.
Da das Skalarprodukt der Vektoren ist, liegen sie orthogonal zueinander.
Punktprobe:
c)
Prüfe, ob die Richtungsvektoren und
der Ebene
orthogonal zum Normalenvektor
der Ebene
liegen.
Da das Skalarprodukt der Vektoren ist, liegen sie orthogonal zueinander.
Punktprobe:
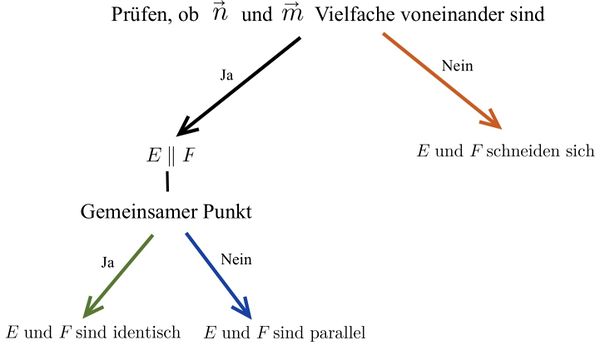
⭐Beide Ebenengleichungen in Koordinatenform
Gegeben sind eine Ebene und eine Ebene
. Untersuche die Lagebeziehung der beiden Ebenen.
1. Schritt: Prüfe, ob der Normalenvektor der Ebene
ein Vielfaches des Normalenvektors
der Ebene
ist.
2. Schritt: Interpretiere die Lösung des LGS.
Da das LGS nicht lösbar ist, sind die beiden Gleichungen linear unabhängig und die Ebenen schneiden sich in einer Schnittgeraden.
3. Schritt: Bestimme die Schnittgerade.
Stelle mit den beiden Ebenengleichungen ein LGS auf und löse es mithilfe des Gauß-Algorithmus oder dem Taschenrechner.
Setze und bestimme
und
.
Stelle die Geradengleichung auf.
Gegeben ist eine Ebene . Untersuche die Lagebeziehung zwischen dieser und den dir angezeigten Ebenen. Ziehe die Ebenen in das entsprechende Feld.
Vergleiche die Gleichungen der zwei Ebenen miteinander. Die Ebenen schneiden sich, wenn die beiden Gleichungen linear unabhängig voneinander sind. Die Ebenen sind parallel, wenn die Normalenvektoren identisch oder Vielfache voneinander sind, aber das LGS keine Lösung besitzt.
DIe Ebenen sind identisch, wenn die Normalenvektoren identisch oder Vielfache voneinander sind und das LGS somit unendlich viele Lösungen hat.
Die beiden Seitenflächen eines Zeltes liegen in den Ebenen und
. Der Erdboden wird durch die
-
-Ebene aufgespannt. In welcher Höhe befindet sich die obere Zeltkante, wenn eine Einheit im Koordinatensystem
cm entspricht?
Die Zeltkante entspricht der Schnittgeraden der beiden Ebenen. Um die Höhe zu bestimmen, benötigt man also den Stützvektor der Geradengleichung der Zeltkante.
Da die Ebenen in Parameterform gegeben sind, setzen wir die Gleichungen zunächst gleich und lösen dann das entsprechende LGS:
und
Einsetzen von in
ergibt:
Die Schnittgerade der beiden Ebenen lautet demnach:
Da die Schnittgerade der oberen Zeltkante entspricht, lässt sich aus dem Stützvektor der Geraden die Höhe ablesen. Die Höhe kann mithilfe der -Koordinate des Vektors bestimmt werden.
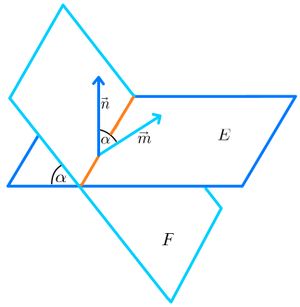
⭐Berechnung des Winkels zwischen Ebene und Ebene
Wenn sich zwei Ebenen schneiden, kann der Schnittwinkel bestimmt werden, den sie einschließen. Wie in Abbildung ... zu sehen ist, kannst du dazu die Normalenvektoren betrachten. Sie schließen denselben Winkel ein, wie die beiden Ebenen. Betrachten wir die Normalenvektoren, so können wir ähnlich vorgehen, wie beim Berechnen des Winkels zwischen zwei Geraden.
Um den Schnittwinkel zu berechnen, musst du zunächst die Normalenvektoren der Ebenen bestimmen. Wenn du nicht mehr genau weißt, wie das geht, schaue nochmal in Kapitel Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum.
Seien und
zwei sich schneidende Ebenen mit den Normalenvektoren
und
. Der Schnittwinkel
zwischen
und
kann mit folgender Formel berechnet werden:
.
Gegeben sind zwei Ebenen und
mit
und
. Berechne den Schnittpunkt zwischen den Ebenen.
1. Schritt: Bestimmte die Normalenvektoren von und
.
Der Normalenvektor von ist
. Der Normalenvektor von
lautet
.
2. Schritt: Einsetzen der Normalenvektoren in die Formel.
3. Schritt: Auflösen der Gleichung.
Sei eine Ebene mit
,
eine Ebene mit
.
und
eine Ebene mit
.
Berechne den Winkel zwischen
a) E und F
Bei der Ebene handelt es sich um die
Ebene. Der Normalenvektor ist also
. Der Normalenvektor der Ebene
kann abgelesen werden:
.
Einsetzen in die Formel liefert:
Nun muss die Formel mit Hilfe des Taschenrechners aufgelöst werden:
b) F und H und
Die Normalenvektor der Ebenen und
können abgelesen werden als
und
Einsetzen in die Formel liefert:
.
Nun muss die Formel mit Hilfe des Taschenrechners aufgelöst werden:
c) E und H.
Bei der Ebene handelt es sich um die
Ebene. Der Normalenvektor ist also
. Der Normalenvektor der Ebene
kann abgelesen werden:
.
Einsetzen in die Formel liefert:
Nun muss die Formel mit Hilfe des Taschenrechners aufgelöst werden:
Der Winkel zwischen den beiden Vektoren und
beträgt
.
Gib die Gleichungen zweier Ebenen und
an, die sich in einem Winkel von
schneiden.
Der Winkel zwischen zwei Ebenen entspricht dem Winkel zwischen ihren Normalenvektoren. Da der Winkel zwischen den beiden angebenen Vektoren und
genau dem Winkel entspricht, den die Ebenen einschließen sollen, können sie als Normalenvektoren der Ebenen verwendet werden. Die Punkte, durch die die Ebenen laufen, können frei gewählt werden.
Eine mögliche Lösung für die Ebenen lautet daher:
An einem Wanderweg soll eine Holzbank aufgestellt werden. Die Bank wird so ausgerichtet, dass die Sitzfläche durch die Ebene und die Rückenlehne durch die Ebene
beschrieben werden kann.
a) Um eine bequeme Sitzposition zu ermöglichen, sollte der Winkel zwischen Rückenlehne und Sitzfläche zwischen und
liegen. Überprüfe, ob dies auf die neue Bank zutrifft.
Als Normalenvektor der Ebene erhält man
und als Normalenvektor der Ebene
.
Einsetzen in die Formel liefert:
Umstellen der Formel ergibt:
b)
Da der Wanderweg sehr beliebt ist, soll noch eine zweite Bank aufgestellt werden. Sie wird so ausgerichtet, dass beide Bänke mit den Rückenlehnen aneinander stehen. Auch bei der zweiten Bank können die Sitzfläche und die Rückenlehne durch Ebenen beschrieben werden. Die Sitzfläche entspricht der Ebene und die Rückenlehne der Ebene
Berechne den Winkel, unter dem die beiden Rückenlehnen der Bänke aufeinander treffen.
Es soll der Winkel zwischen den beiden Rückenlehnen und
berechnet werden.
Die Normalenvektoren der Ebenen lauten und
.
Einsetzen in die Formel liefert: