Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 80: | Zeile 80: | ||
{{Box|Aufgabe 2: Untersuchung der Lagebeziehung zwischen Gerade und Ebene| | {{Box|Aufgabe 2: Untersuchung der Lagebeziehung zwischen Gerade und Ebene| | ||
Gegeben ist eine Ebene <math>E: \vec{x}=\left( \begin{matrix} 1\\ 0\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} -1\\ 1\\ 0 \end{matrix} \right) + t \cdot \left( \begin{matrix} -1\\ 0\\ 1 \end{matrix} \right) </math>. | Gegeben ist eine Ebene <math>E: \vec{x}=\left( \begin{matrix} 1\\ 0\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} -1\\ 1\\ 0 \end{matrix} \right) + t \cdot \left( \begin{matrix} -1\\ 0\\ 1 \end{matrix} \right) </math>. Untersuche die Lagebeziehung zwischen dieser Ebene und den untenstehenden Geraden. Ziehe die Geraden in das entsprechende Feld. | ||
{{LearningApp|width=100%|height=500px|app=ph1zptuwk21}} | {{LearningApp|width=100%|height=500px|app=ph1zptuwk21}} | ||
| Zeile 303: | Zeile 303: | ||
===Mögliche Lagebeziehungen zwischen zwei Ebenen=== | ===Mögliche Lagebeziehungen zwischen zwei Ebenen=== | ||
{{Box|Merke:| | {{Box|Merke:| | ||
Zwischen zwei Ebenen gibt es drei mögliche Lagebeziehungen | Zwischen zwei Ebenen gibt es drei mögliche Lagebeziehungen: | ||
{{3Spalten | {{3Spalten | ||
| | | | ||
| Zeile 319: | Zeile 319: | ||
Die Ebenen sind parallel. | Die Ebenen sind parallel. | ||
| | | | ||
Die | Die Ebenen sind identisch. | ||
}} | }} | ||
|Merksatz}} | |Merksatz}} | ||
{{Box|Aufgabe: Lückentext zur Lagebeziehung zwischen Ebene und Ebene| | {{Box|Aufgabe 8: Lückentext zur Lagebeziehung zwischen Ebene und Ebene| | ||
{{LearningApp|width=100%|height=500px|app=ptpaywm2521}} | {{LearningApp|width=100%|height=500px|app=ptpaywm2521}} | ||
| Zeile 330: | Zeile 330: | ||
===Untersuchung der Lagebeziehung von zwei Ebenen=== | ===Untersuchung der Lagebeziehung von zwei Ebenen=== | ||
==== | ====Beide Ebenengleichungen in Parameterform==== | ||
{{Box|Merke: Lagebeziehung von zwei Ebenen in Parameterform untersuchen. | | {{Box|Merke: Lagebeziehung von zwei Ebenen in Parameterform untersuchen. | | ||
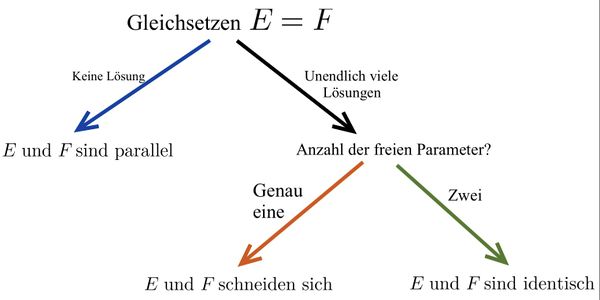
[[Datei:Vorgehen zur Berechnung der Lagebeziehung von Ebenen in Parameterform.jpg|zentriert|rahmenlos|600x600px]] | [[Datei:Vorgehen zur Berechnung der Lagebeziehung von Ebenen in Parameterform.jpg|zentriert|rahmenlos|600x600px]] | ||
| Zeile 336: | Zeile 336: | ||
{{Box | | {{Box | Beispiel: Untersuchung der Lagebeziehung von zwei Ebenen in Parameterform | | ||
Gegeben sind eine Ebene <math>E: \vec{x}=\left( \begin{matrix} 1\\ 4\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} 1\\ -2\\ 1 \end{matrix} \right) + t \cdot \left( \begin{matrix} 3\\ 1\\ -1 \end{matrix} \right) </math> und eine Ebene <math>F: \vec{x}=\left( \begin{matrix} 1\\ 2\\ 3 \end{matrix} \right) + r \cdot \left( \begin{matrix} 2\\ 3\\ -2 \end{matrix} \right)+ u \cdot \left( \begin{matrix} 5\\ 4\\ -3 \end{matrix} \right)</math>. | Gegeben sind eine Ebene <math>E: \vec{x}=\left( \begin{matrix} 1\\ 4\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} 1\\ -2\\ 1 \end{matrix} \right) + t \cdot \left( \begin{matrix} 3\\ 1\\ -1 \end{matrix} \right) </math> und eine Ebene <math>F: \vec{x}=\left( \begin{matrix} 1\\ 2\\ 3 \end{matrix} \right) + r \cdot \left( \begin{matrix} 2\\ 3\\ -2 \end{matrix} \right)+ u \cdot \left( \begin{matrix} 5\\ 4\\ -3 \end{matrix} \right)</math>. | ||
| Zeile 362: | Zeile 362: | ||
'''4. Schritt:''' Interpretiere die Lösung des Gleichungssystems: | '''4. Schritt:''' Interpretiere die Lösung des Gleichungssystems: | ||
In der dritten Zeile der Lösungsmatrix befindet sich ein Widerspruch. Somit hat das LGS keine Lösung und die beiden Ebenen sind parallel | In der dritten Zeile der Lösungsmatrix befindet sich ein Widerspruch. Somit hat das LGS keine Lösung und die beiden Ebenen sind parallel. | ||
| Hervorhebung1}} | | Hervorhebung1}} | ||
{{Box|Aufgabe: Ergebnisse interpretieren| | {{Box|Aufgabe 9: Ergebnisse interpretieren| | ||
Interpretiere die jeweilige Situation geometrisch. | Interpretiere die jeweilige Situation geometrisch. | ||
| Zeile 375: | Zeile 375: | ||
'''a)''' <math>\begin{vmatrix} 1 & 0 & 0 & -0,5 & 0,5 \\ 0 & 1 & 0 & -1 & 0,5 \\ 0 & 0 & 1 & 1,5 & 1 \end{vmatrix}</math> | '''a)''' <math>\begin{vmatrix} 1 & 0 & 0 & -0,5 & 0,5 \\ 0 & 1 & 0 & -1 & 0,5 \\ 0 & 0 & 1 & 1,5 & 1 \end{vmatrix}</math> | ||
{{Lösung versteckt|1=Das Gleichungssystem besitzt unendlich viele Lösungen. Da sich in jeder Zeile der Diagonalform Einträge befinden, schneiden sich | {{Lösung versteckt|1=Das Gleichungssystem besitzt unendlich viele Lösungen. Da sich in jeder Zeile der Diagonalform Einträge befinden, ist nur ein Parameter frei wählbar und die Ebenen schneiden sich in einer Schnittgeraden.|2=Lösung anzeigen|3=Lösung verbergen}} | ||
'''b)''' <math>\begin{vmatrix} 1 & 3 & -2 & 5 & 0 \\ 0 & 7 & -7 & -14 & -2 \\ 0 & 0 & 0 & 0 & -13 \end{vmatrix}</math> | '''b)''' <math>\begin{vmatrix} 1 & 3 & -2 & 5 & 0 \\ 0 & 7 & -7 & -14 & -2 \\ 0 & 0 & 0 & 0 & -13 \end{vmatrix}</math> | ||
| Zeile 387: | Zeile 387: | ||
|Arbeitsmethode}} | |Arbeitsmethode}} | ||
==== | ====⭐Ebenengleichungen in Parameter- und Koordinatenform==== | ||
{{Box|Merke: Lagebeziehung von zwei Ebenen in Koordinatenform und Parameterform untersuchen. | | {{Box|Merke: Lagebeziehung von zwei Ebenen in Koordinatenform und Parameterform untersuchen. | | ||
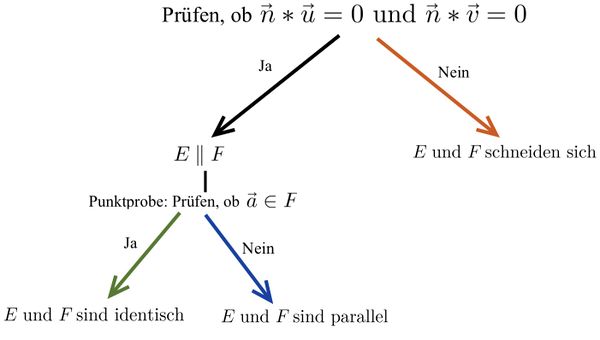
[[Datei:Vorgehen zur Untersuchung der Lagebeziehung von zwei Ebenen.jpg|zentriert|rahmenlos|600x600px]] | [[Datei:Vorgehen zur Untersuchung der Lagebeziehung von zwei Ebenen.jpg|zentriert|rahmenlos|600x600px]] | ||
|Merksatz}} | |Merksatz}} | ||
{{Box | | {{Box | Beispiel: Untersuchung der Lagebeziehung von zwei Ebenen in Koordinatenform und Parameterform | | ||
Gegeben sind eine Ebene <math>E: \vec{x}=\left( \begin{matrix} 2\\ 1\\ -3 \end{matrix} \right) + r \cdot \left( \begin{matrix} 1\\ 0\\ -1 \end{matrix} \right) + s \cdot \left( \begin{matrix} 2\\ 1\\ 0 \end{matrix} \right) </math> und eine Ebene <math>F: -1{,}5x_1+3x_2-1{,}5x_3=4,5</math>. | Gegeben sind eine Ebene <math>E: \vec{x}=\left( \begin{matrix} 2\\ 1\\ -3 \end{matrix} \right) + r \cdot \left( \begin{matrix} 1\\ 0\\ -1 \end{matrix} \right) + s \cdot \left( \begin{matrix} 2\\ 1\\ 0 \end{matrix} \right) </math> und eine Ebene <math>F: -1{,}5x_1+3x_2-1{,}5x_3=4,5</math>. | ||
| Zeile 400: | Zeile 400: | ||
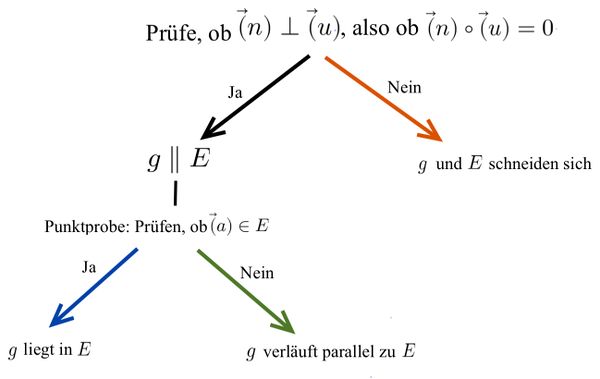
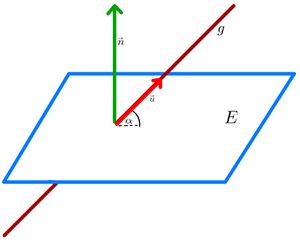
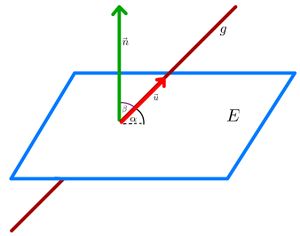
'''1. Schritt:''' Prüfe, ob die Richtungsvektoren <math> \vec{u}</math> und <math> \vec{v} </math> der Ebene <math>E </math> orthogonal zum Normalenvektor <math> \vec{v}</math> der Ebene <math>F</math> liegen. | '''1. Schritt:''' Prüfe, ob die Richtungsvektoren <math> \vec{u}</math> und <math> \vec{v} </math> der Ebene <math>E </math> orthogonal zum Normalenvektor <math> \vec{v}</math> der Ebene <math>F</math> liegen. | ||
Hierfür muss gelten, dass <math> \vec{n} \ | Hierfür muss gelten, dass <math> \vec{n} \ast \vec{u}=0</math> und <math> \vec{n} \ast \vec{v}=0</math>. | ||
<math> \vec{n} \ | <math> \vec{n} \ast \vec{u}=\left( \begin{matrix} -1{,}5\\ 3\\ -1{,}5 \end{matrix} \right)\ast\left( \begin{matrix} 1\\ 0\\ -1 \end{matrix} \right)=-1,5+0+1,5=0</math> | ||
<math> \vec{n} \ | <math> \vec{n} \ast \vec{v}=\left( \begin{matrix} -1{,}5\\ 3\\ -1{,}5 \end{matrix} \right)\ast\left( \begin{matrix} 2\\ 1\\ 0 \end{matrix} \right)=-3+3+0=0</math> | ||
| Zeile 410: | Zeile 410: | ||
'''2.Schritt:''' Interpretiere die Lösung des Skalarproduktes: | '''2.Schritt:''' Interpretiere die Lösung des Skalarproduktes: | ||
Da das Skalarprodukt der Vektoren 0 ist, liegen sie orthogonal zueinander. Das bedeutet, | Da das Skalarprodukt der Vektoren <math>0</math> ist, liegen sie orthogonal zueinander. Das bedeutet, dass die Ebenen sich nicht in einer Schnittgeraden schneiden, sondern entweder identisch oder parallel sind. | ||
| Zeile 426: | Zeile 426: | ||
| Hervorhebung1}} | | Hervorhebung1}} | ||
{{Box|Aufgabe: Lagebeziehungen berechnen| | {{Box|Aufgabe 10: Lagebeziehungen berechnen| | ||
Untersuche die Lagebeziehung der jeweiligen Ebenen. | Untersuche die Lagebeziehung der jeweiligen Ebenen. | ||
| Zeile 454: | Zeile 454: | ||
|Arbeitsmethode}} | |Arbeitsmethode}} | ||
==== | ====⭐Beide Ebenengleichungen in Koordinatenform==== | ||
{{Box|Merke: Lagebeziehung von zwei Ebenen in Koordinatenform | {{Box|Merke: Untersuchung der Lagebeziehung von zwei Ebenen in Koordinatenform | | ||
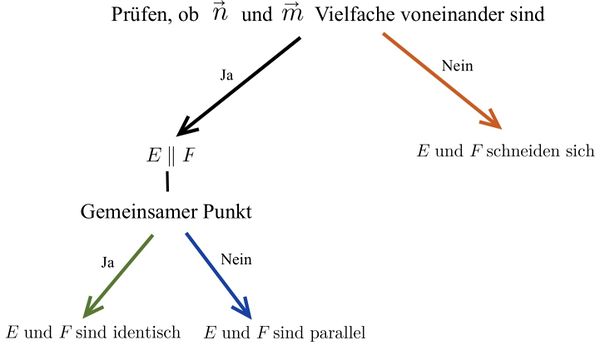
[[Datei:Vorgehen zur Untersuchung der Lagebeziehung von Ebenen in Koordinatenform.jpg|zentriert|rahmenlos|600x600px]] | [[Datei:Vorgehen zur Untersuchung der Lagebeziehung von Ebenen in Koordinatenform.jpg|zentriert|rahmenlos|600x600px]] | ||
|Merksatz}} | |Merksatz}} | ||
{{Box | | {{Box | Beispiel: Untersuchung der Lagebeziehung von zwei Ebenen in Koordinatenform | | ||
Gegeben sind eine Ebene <math>E:3x_1-4x_2-x_3=4 </math> und eine Ebene <math>F: 3x_1-3x_2+x_3=3</math>. Untersuche die Lagebeziehung der beiden Ebenen. | Gegeben sind eine Ebene <math>E:3x_1-4x_2-x_3=4 </math> und eine Ebene <math>F: 3x_1-3x_2+x_3=3</math>. Untersuche die Lagebeziehung der beiden Ebenen. | ||
| Zeile 491: | Zeile 491: | ||
<math>g: \vec{x} = \begin{pmatrix} 0 \\ -1 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} -\frac{7}{3} \\ -2 \\ 1 \end{pmatrix} </math>| Hervorhebung1}} | <math>g: \vec{x} = \begin{pmatrix} 0 \\ -1 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} -\frac{7}{3} \\ -2 \\ 1 \end{pmatrix} </math>| Hervorhebung1}} | ||
{{Box|Aufgabe: Untersuchung der Lagebeziehung zwischen zwei Ebenen in Koordinatenform | | {{Box|Aufgabe 11: Untersuchung der Lagebeziehung zwischen zwei Ebenen in Koordinatenform | | ||
Gegeben ist eine Ebene <math>E: \vec{x}=-2x_1-3x_2+x_3=2 </math>. | Gegeben ist eine Ebene <math>E: \vec{x}=-2x_1-3x_2+x_3=2 </math>. | ||
| Zeile 507: | Zeile 507: | ||
|Arbeitsmethode}} | |Arbeitsmethode}} | ||
{{Box|Aufgabe: Schnitt von zwei Zeltflächen| | {{Box|Aufgabe 12: Schnitt von zwei Zeltflächen| | ||
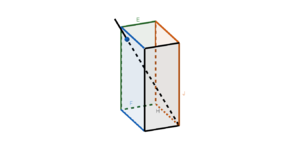
Die beiden Seitenflächen eines Zeltes liegen in den Ebenen <math>E: \vec{x} = \begin{pmatrix} 8 \\ 0 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 3 \\ 4\end{pmatrix | Die beiden Seitenflächen eines Zeltes liegen in den Ebenen <math>E: \vec{x} = \begin{pmatrix} 8 \\ 0 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 3 \\ 4\end{pmatrix} </math> und <math>F: \vec{x} = \begin{pmatrix} 8 \\ 6 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix}+ u \cdot \begin{pmatrix} 0 \\ -3 \\ 4 \end{pmatrix}</math>. Der Erdboden wird durch die <math>x_1</math>-<math>x_2</math> -Ebene aufgespannt. In welcher Höhe befindet sich die obere Zeltkante, wenn eine Einheit im Koordinatensystem <math>1</math> m entspricht? | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= Mache dir zunächst eine Skizze von der Situation. Überlege dir, womit die obere Zeltkante beschrieben werden kann.|2=Tipp 1 anzeigen|3=Tipp 1 verbergen}} | ||
{{Lösung versteckt|1= Die obere Zeltkante entspricht der Schnittgeraden der beiden Ebenen. |2=Tipp 2 anzeigen|3=Tipp 2 verbergen}} | {{Lösung versteckt|1= Die obere Zeltkante entspricht der Schnittgeraden der beiden Ebenen. |2=Tipp 2 anzeigen|3=Tipp 2 verbergen}} | ||
{{Lösung versteckt|1= Die Höhe der Zeltkante kannst du mithilfe des Stützvektors der | {{Lösung versteckt|1= Die Höhe der Zeltkante kannst du mithilfe des Stützvektors der Schnittgeraden ermitteln. |2=Tipp 2 anzeigen|3=Tipp 2 verbergen}} | ||
{{Lösung versteckt|1= Die Zeltkante entspricht der Schnittgeraden der beiden Ebenen. Um die Höhe zu bestimmen, benötigt man also den Stützvektor der Geradengleichung der Zeltkante. | {{Lösung versteckt|1= Die Zeltkante entspricht der Schnittgeraden der beiden Ebenen. Um die Höhe zu bestimmen, benötigt man also den Stützvektor der Geradengleichung der Zeltkante. | ||
| Zeile 529: | Zeile 529: | ||
<math> g: \vec{x} = \left( \begin{matrix} 3\\ 0\\ 2 \end{matrix} \right) + t \cdot \left( \begin{matrix} -3\\ 5\\ {-}1 \end{matrix} \right) </math> | <math> g: \vec{x} = \left( \begin{matrix} 3\\ 0\\ 2 \end{matrix} \right) + t \cdot \left( \begin{matrix} -3\\ 5\\ {-}1 \end{matrix} \right) </math> | ||
Da die Schnittgerade der oberen Zeltkante entspricht, lässt sich aus dem Stützvektor der Geraden die Höhe ablesen. | Da die Schnittgerade der oberen Zeltkante entspricht, lässt sich aus dem Stützvektor der Geraden die Höhe ablesen. Die Höhe entspricht der <math>x_3</math>-Koordinate des Vektors und somit der <math>4</math>. | ||
Die obere Zeltkante befindet sich also in | Die obere Zeltkante befindet sich also in <math>4</math> m Höhe. | ||
|2=Lösung anzeigen|3=Lösung verbergen}} | |2=Lösung anzeigen|3=Lösung verbergen}} | ||
Version vom 9. Mai 2021, 10:16 Uhr
Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".
Das Lernpfadkapitel ist so aufgebaut, dass ihr in jedem Abschnitt zuerst grundlegende Inhalte mithilfe der Merkkästen wiederholen könnt. Anschließend findet ihr eine Beispielaufgabe, in der die Inhalte veranschaulicht werden. Am Ende jedes Abschnittes gibt es Übungsaufgaben mit Tipps und Lösungen, sodass ihr üben und euch selbst überprüfen könnt.
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
Untersuchung der Lagebeziehung zwischen Gerade und Ebene
⭐Berechnung des Winkels zwischen Gerade und Ebene
Lagebeziehung Ebene-Ebene
Mögliche Lagebeziehungen zwischen zwei Ebenen
Untersuchung der Lagebeziehung von zwei Ebenen
Beide Ebenengleichungen in Parameterform
⭐Ebenengleichungen in Parameter- und Koordinatenform
⭐Beide Ebenengleichungen in Koordinatenform
⭐Berechnung des Winkels zwischen Ebene und Ebene