Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Marie (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 198: | Zeile 198: | ||
===⭐Berechnung des Winkels zwischen Gerade und Ebene=== | ===⭐Berechnung des Winkels zwischen Gerade und Ebene=== | ||
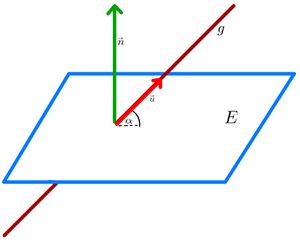
[[Datei:Abbildung | [[Datei:Abbildung Winkel zwischen Gerade und Ebene .jpg|mini|Abbildung: Winkel zwischen Gerade und Ebene]] | ||
{{Box | Erläuterung: Winkel berechnen zwischen Gerade und Ebene | Wenn eine Gerade g eine Eben E schneidet, kannst du nicht nur den Schnittpunkt berechnen, sondern auch den Schnittwinkel. Dafür benötigen wir den Normalenvektor. Wenn du nicht mehr genau weißt, wie man diesen abliest oder berechnet, schau noch einmal in Kapitel... | Merksatz}} | {{Box | Erläuterung: Winkel berechnen zwischen Gerade und Ebene | Wenn eine Gerade g eine Eben E schneidet, kannst du nicht nur den Schnittpunkt berechnen, sondern auch den Schnittwinkel. Dafür benötigen wir den Normalenvektor. Wenn du nicht mehr genau weißt, wie man diesen abliest oder berechnet, schau noch einmal in Kapitel... | Merksatz}} | ||
| Zeile 208: | Zeile 208: | ||
Wenn du wissen möchtest, warum du nicht wie beim Winkel zwischen zwei Geraden den Kosinus benutzt, kannst du das hier nachlesen: | Wenn du wissen möchtest, warum du nicht wie beim Winkel zwischen zwei Geraden den Kosinus benutzt, kannst du das hier nachlesen: | ||
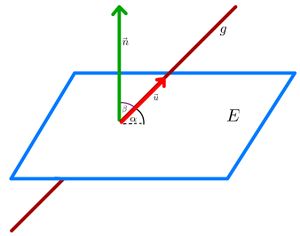
{{Lösung versteckt|1=Der Normalenvektor <math>\vec{n}</math> einer Ebene steht in einem 90 Winkel zur Ebene <math>E</math>. Wenn wir den Winkel zwischen einer Gerade <math>g</math> und einer <math>E</math> berechnen wollen, können wir wie beim Winkel zwischen zwei Geraden mit der Kosinusfunktion den Winkel zwischen dem Richtungsvektor von <math>g</math> und dem Normalenvektor von <math>E</math> berechnen. In Abbildung ... ist dieser Winkel mit <math>\beta</math> bezeichnet. Um nun den Winkel <math>\alpha</math> zwischen <math>g</math> und <math>E</math> zu erhalten, müssen wir <math>\beta</math> von <math> 90 ^\circ </math> abziehen. Dies entspricht der obigen Formel mit der Sinusfunktion.|2=Erklärung anzeigen|3=Erklärung verbergen}} | {{Lösung versteckt|1= | ||
[[Datei:Abbildung- Winkel zwischen Gerade und Ebene, Zusammenhang zum Normalenvektor.jpg|mini|Abbildung: Winkel zwischen Gerade und Ebene, Zusammenhang zum Normalenvektor]] | |||
Der Normalenvektor <math>\vec{n}</math> einer Ebene steht in einem 90 Winkel zur Ebene <math>E</math>. Wenn wir den Winkel zwischen einer Gerade <math>g</math> und einer <math>E</math> berechnen wollen, können wir wie beim Winkel zwischen zwei Geraden mit der Kosinusfunktion den Winkel zwischen dem Richtungsvektor von <math>g</math> und dem Normalenvektor von <math>E</math> berechnen. In Abbildung ... ist dieser Winkel mit <math>\beta</math> bezeichnet. Um nun den Winkel <math>\alpha</math> zwischen <math>g</math> und <math>E</math> zu erhalten, müssen wir <math>\beta</math> von <math> 90 ^\circ </math> abziehen. Dies entspricht der obigen Formel mit der Sinusfunktion.|2=Erklärung anzeigen|3=Erklärung verbergen}} | |||
| Merksatz}} | | Merksatz}} | ||
Version vom 8. Mai 2021, 18:41 Uhr
Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
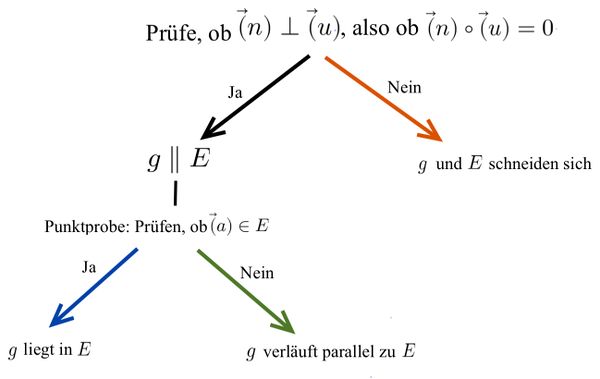
Untersuchung der Lagebeziehung zwischen Gerade und Ebene
⭐Berechnung des Winkels zwischen Gerade und Ebene
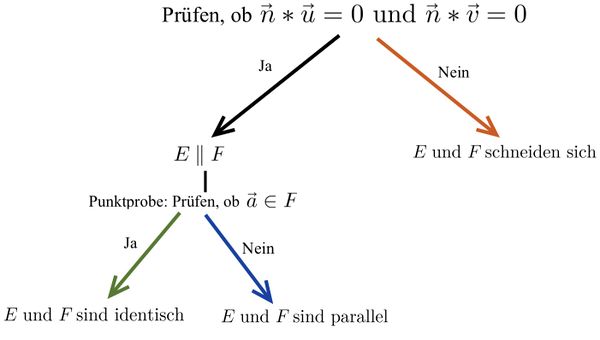
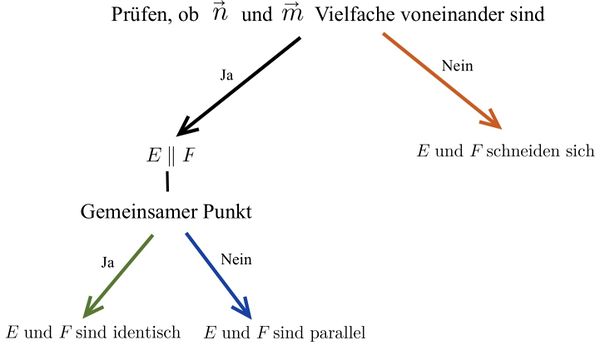
Lagebeziehung Ebene-Ebene
Mögliche Lagebeziehungen zwischen zwei Ebenen
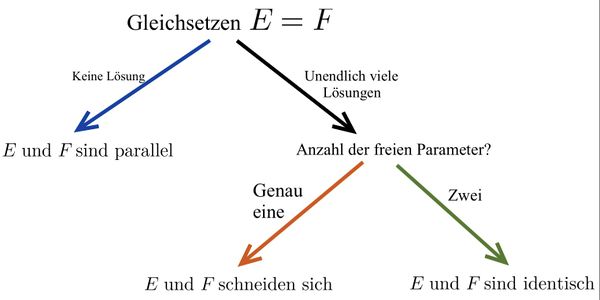
Untersuchung der Lagebeziehung von zwei Ebenen
Zwei Ebenengleichungen in Parameterform
Eine Ebenengleichungen in Parameterform – eine Ebenengleichung in Koordinatenform
Zwei Ebenengleichungen in Koordinatenform
⭐Berechnung des Winkels zwischen Ebene und Ebene