Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Marie (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Marie (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 282: | Zeile 282: | ||
{{LearningApp|width=100%|height=500px|app=ptpaywm2521}} | {{LearningApp|width=100%|height=500px|app=ptpaywm2521}} | ||
|Arbeitsmethode}} | |Arbeitsmethode| Farbe={{Farbe|orange}}}} | ||
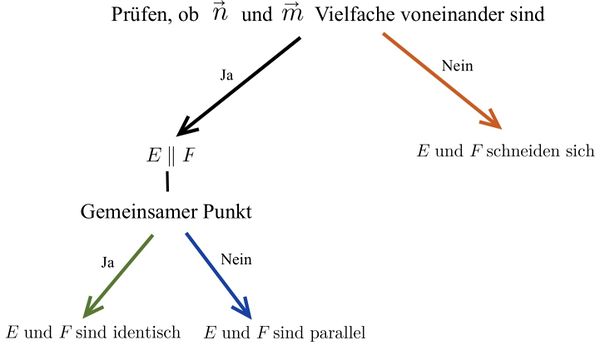
===Untersuchung der Lagebeziehung von zwei Ebenen=== | ===Untersuchung der Lagebeziehung von zwei Ebenen=== | ||
| Zeile 379: | Zeile 379: | ||
Da der Aufpunkt die Koordinatengleichung von <math>F</math> erfüllt, liegt <math>E</math> in <math>F</math> und die Ebenen sind identisch. | Da der Aufpunkt die Koordinatengleichung von <math>F</math> erfüllt, liegt <math>E</math> in <math>F</math> und die Ebenen sind identisch. | ||
| Hervorhebung1}} | | Hervorhebung1}} | ||
| Zeile 425: | Zeile 422: | ||
'''3. Schritt:''' Bestimme die Schnittgerade. | '''3. Schritt:''' Bestimme die Schnittgerade. | ||
Stelle mit den beiden Ebenengleichungen ein LGS auf und löse es mithilfe des Gauß- | Stelle mit den beiden Ebenengleichungen ein LGS auf und löse es mithilfe des Gauß-Algorithmus oder dem Taschenrechner. | ||
<math> \begin{vmatrix} 3 & -4 & -1 & 4 \\ 3 & -3 & 1 & 3 \end{vmatrix} \Leftrightarrow \begin{vmatrix} 3 & -4 & -1 & 4 \\ 0 & 1 & 2 & -1 \end{vmatrix}</math> | <math> \begin{vmatrix} 3 & -4 & -1 & 4 \\ 3 & -3 & 1 & 3 \end{vmatrix} \Leftrightarrow \begin{vmatrix} 3 & -4 & -1 & 4 \\ 0 & 1 & 2 & -1 \end{vmatrix}</math> | ||
| Zeile 437: | Zeile 434: | ||
Stelle die Geradengleichung auf. | Stelle die Geradengleichung auf. | ||
<math>g: \vec{x} = \begin{pmatrix} 0 \\ -1 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} -\frac{7}{3} \\ -2 \\ 1 \end{pmatrix} </math> | <math>g: \vec{x} = \begin{pmatrix} 0 \\ -1 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} -\frac{7}{3} \\ -2 \\ 1 \end{pmatrix} </math>| Hervorhebung1}} | ||
| Hervorhebung1}} | |||
{{Box|Aufgabe: Untersuchung der Lagebeziehung zwischen zwei Ebenen in Koordinatenform | | {{Box|Aufgabe: Untersuchung der Lagebeziehung zwischen zwei Ebenen in Koordinatenform | | ||
| Zeile 463: | Zeile 454: | ||
{{Box|Aufgabe: Schnitt von zwei Zeltflächen| | {{Box|Aufgabe: Schnitt von zwei Zeltflächen| | ||
Die beiden Seitenflächen eines Zeltes liegen in den Ebenen <math>E: | Die beiden Seitenflächen eines Zeltes liegen in den Ebenen <math>E:-27x_1+9x_2+10x_3=23 </math> und <math>F: \vec{x} = \begin{pmatrix} -5 \\ 2 \\ -13 \end{pmatrix} + t \cdot \begin{pmatrix} 6 \\ -2 \\ 18 \end{pmatrix}+ u \cdot \begin{pmatrix} -54 \\ 18 \\ 20 \end{pmatrix}, t,u \in \mathbb{R} </math>. Berechne die Geradengleichung der oberen Zeltkante. | ||
|Arbeitsmethode}} | {{Lösung versteckt|1= | ||
|2=Lösung anzeigen|3=Lösung verbergen}} | |||
|Arbeitsmethode| Farbe={{Farbe|blau}}}} | |||
===⭐Berechnung des Winkels zwischen Ebene und Ebene=== | ===⭐Berechnung des Winkels zwischen Ebene und Ebene=== | ||
Version vom 8. Mai 2021, 17:13 Uhr
Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".
Lagebeziehung Gerade-Ebene
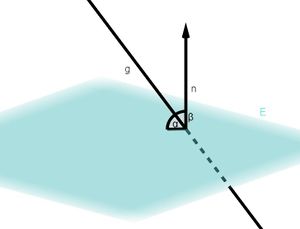
Mögliche Lagebeziehungen zwischen Gerade und Ebene
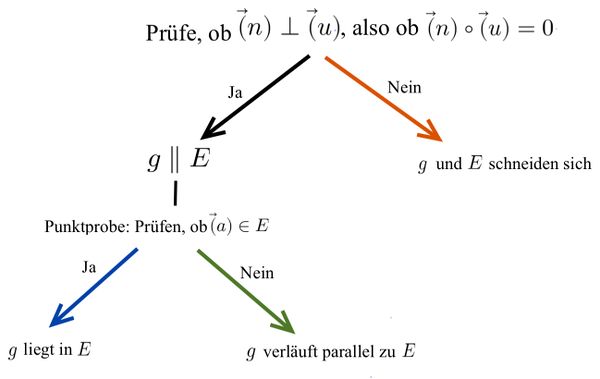
Untersuchung der Lagebeziehung zwischen Gerade und Ebene
⭐Berechnung des Winkels zwischen Gerade und Ebene
Lagebeziehung Ebene-Ebene
Mögliche Lagebeziehungen zwischen zwei Ebenen
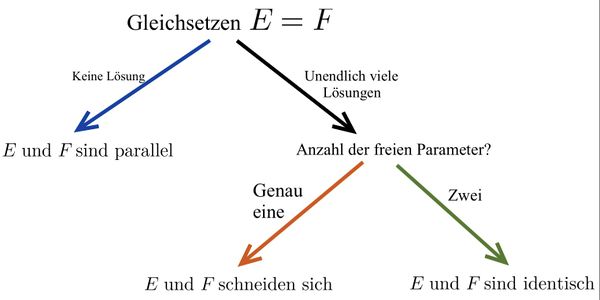
Untersuchung der Lagebeziehung von zwei Ebenen
Zwei Ebenengleichungen in Parameterform
Eine Ebenengleichungen in Parameterform – eine Ebenengleichung in Koordinatenform
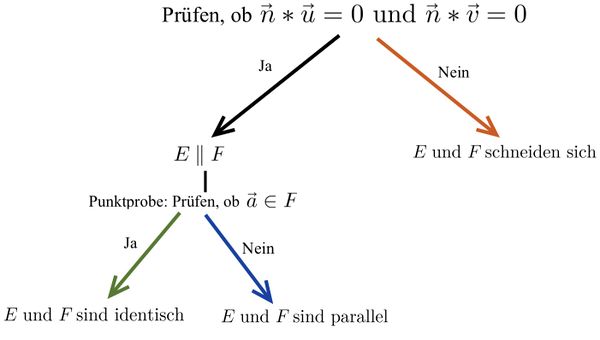
Zwei Ebenengleichungen in Koordinatenform
⭐Berechnung des Winkels zwischen Ebene und Ebene