Benutzer:Buss-Haskert/Gleichungen/Anwendungsaufgaben: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 1: | Zeile 1: | ||
SEITE IM AUFBAU! | SEITE IM AUFBAU!! | ||
{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | |||
<br> | |||
{{Navigation|[[Benutzer:Buss-Haskert/Gleichungen|Gleichungen - Halte die Waage im Gleichgewicht]]<br> | {{Navigation|[[Benutzer:Buss-Haskert/Gleichungen|Gleichungen - Halte die Waage im Gleichgewicht]]<br> | ||
[[Benutzer:Buss-Haskert/Gleichungen/Was ist eine Gleichung|1.1) Was ist eine Gleichung]]<br> | [[Benutzer:Buss-Haskert/Gleichungen/Was ist eine Gleichung|1.1) Was ist eine Gleichung]]<br> | ||
[[Benutzer:Buss-Haskert/Gleichungen/Was ist eine Gleichung|1.2) Gleichungen lösen durch Probieren]]<br> | [[Benutzer:Buss-Haskert/Gleichungen/Was ist eine Gleichung|1.2) Gleichungen lösen durch Probieren]]<br> | ||
[[Benutzer:Buss-Haskert/Gleichungen/Gleichungen lösen|2) Gleichungen lösen durch Umformen]]<br> | [[Benutzer:Buss-Haskert/Gleichungen/Gleichungen lösen|2) Gleichungen lösen durch Umformen]]<br> | ||
[[Benutzer:Buss-Haskert/Gleichungen/ | [[Benutzer:Buss-Haskert/Gleichungen/Gleichungen mit Klammern|3) Gleichungen mit Klammern]]<br> | ||
[[Benutzer:Buss-Haskert/Gleichungen/ | [[Benutzer:Buss-Haskert/Gleichungen/Anwendungsaufgaben|4) Anwendungsaufgaben]]}} | ||
<br> | |||
=== | ===4) Anwendungsaufgaben zu Gleichungen=== | ||
Es gibt verschiedene Bereiche, in denen Gleichungen mit Klammern Anwendung finden: | Es gibt verschiedene Bereiche, in denen Gleichungen mit Klammern Anwendung finden: | ||
| Zeile 71: | Zeile 73: | ||
Diese 6 Schritte helfen dir beim Lösen der Anwendungsaufgaben. Beachte vor allem die Schritte 1 und 2. Notiere genau, welche Bedeutung die Variable hat und stelle die Terme passend zum Text auf. Dann schaffst es es sicherlich auch, eine Gleichung aufzustellen und diese zu lösen. | Diese 6 Schritte helfen dir beim Lösen der Anwendungsaufgaben. Beachte vor allem die Schritte 1 und 2. Notiere genau, welche Bedeutung die Variable hat und stelle die Terme passend zum Text auf. Dann schaffst es es sicherlich auch, eine Gleichung aufzustellen und diese zu lösen. | ||
==== | ====4.1 Mathematische Texte==== | ||
{{Box|Übung 1|Wiederhole das Aufstellen von Termen. Löse dazu die nachfolgenden LearningApps.|Üben}} | {{Box|Übung 1|Wiederhole das Aufstellen von Termen. Löse dazu die nachfolgenden LearningApps.|Üben}} | ||
{{LearningApp|app=pr2s6mz4n20|width=100%|height=400px}} | {{LearningApp|app=pr2s6mz4n20|width=100%|height=400px}} | ||
| Zeile 121: | Zeile 123: | ||
|Üben}} | |Üben}} | ||
==== | ====4.2) Geometrische Texte==== | ||
{{Box|Übung 5|Wiederhole das Aufstellen von Termen. Löse dazu die nachfolgenden LearningApp.|Üben}} | {{Box|Übung 5|Wiederhole das Aufstellen von Termen. Löse dazu die nachfolgenden LearningApp.|Üben}} | ||
{{LearningApp|app=pvyyg1j2a19|width=100%|height=400px}} | {{LearningApp|app=pvyyg1j2a19|width=100%|height=400px}} | ||
| Zeile 135: | Zeile 137: | ||
|Üben}} | |Üben}} | ||
==== | ====4.3 Sachsituationen==== | ||
{{Box|Übung 11|Wiederhole das Aufstellen von Termen. Löse dazu die nachfolgenden LearningApp.|Üben}} | {{Box|Übung 11|Wiederhole das Aufstellen von Termen. Löse dazu die nachfolgenden LearningApp.|Üben}} | ||
{{LearningApp|app=pbwn2x6bj20|width=100%|height=400px}} | {{LearningApp|app=pbwn2x6bj20|width=100%|height=400px}} | ||
Version vom 8. Mai 2021, 11:49 Uhr
SEITE IM AUFBAU!!
1.1) Was ist eine Gleichung
1.2) Gleichungen lösen durch Probieren
2) Gleichungen lösen durch Umformen
3) Gleichungen mit Klammern
4) Anwendungsaufgaben zu Gleichungen
Es gibt verschiedene Bereiche, in denen Gleichungen mit Klammern Anwendung finden:
Bist du fit? Vorübungen
Addition: 1. Summand + 2. Summand = Wert derSumme
Subtraktion: Minuend - Subtrahend = Wert der Differenz
Multiplikation: 1. Faktor ∙ 2. Faktor = Wert des Produktes
Division: Dividend: Divisor = Wert des Quotienten
| Addition | addieren | vermehren | plus | |
| Subtraktion | subtrahieren | vermindern | minus | |
| Multiplikation | multiplizieren | verdoppeln | vervielfachen | mal |
| Division | dividieren | halbieren | teilen | geteilt |
Schreibe über den Aufgabentext die passenden Rechenzeichen. Dies hilft dir beim Aufstellen der Terme.
| Quadrat | u = 4·a | A = a² | ||
| Rechteck | u = 2a + 2b | A = a·b | ||
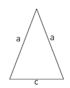
| gleichschenkliges Dreieck | u = 2a + c | 2 gleich lange Seiten | α+β+γ=180° | |
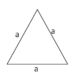
| gleichseitiges Dreieck | u = 3a | 3 gleich lange Seiten | α+β+γ=180° |
In allen Anwendungsbereichen ist es wichtig, dass du den Text genau liest, dir die Situation vorstellst und mit eigenen Worten beschreibst.
6-Schritte-Verfahren für Anwendungsaufgaben
Diese 6 Schritte helfen dir beim Lösen der Anwendungsaufgaben. Beachte vor allem die Schritte 1 und 2. Notiere genau, welche Bedeutung die Variable hat und stelle die Terme passend zum Text auf. Dann schaffst es es sicherlich auch, eine Gleichung aufzustellen und diese zu lösen.
4.1 Mathematische Texte
1. Schritt: Bedeutung der Variablen angeben:
2. Schritt: Terme aufstellen:
"das Vierfache einer Zahl" — 4x
3. Schritt: Gleichung aufstellen:
4. Schritt: Gleichung lösen:
4x = 96 |:4
5. Schritt: Lösung prüfen:
x=24 einsetzen:
4·24 = 96
6. Schritt: Antwort:
1. Schritt: Bedeutung der Variablen angeben:
2. Schritt: Terme aufstellen:
"Vermindert... um 4" — x-4
3. Schritt: Gleichung aufstellen:
4. Schritt: Gleichung lösen:
x-4 = -2 |+4
5. Schritt: Lösung prüfen:
x=2 einsetzen:
2-4 = -2
6. Schritt: Antwort:
4.2) Geometrische Texte
4.3 Sachsituationen
IDEENSAMMLUNG Lernpfad zum Textaufgaben https://unterrichten.zum.de/wiki/Textaufgaben
- ↑ Das Buch "Mathematik real 8 - Differenzierende Ausgabe" aus dem Cornelsenverlag verwendet ebenfalls dieses Verfahren zur Lösung von Sachaufgaben.