Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Marie (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| Zeile 291: | Zeile 291: | ||
{{Box | Beispielaufgabe: Untersuchung der Lagebeziehung von zwei Ebenen in Parameterform | | {{Box | Beispielaufgabe: Untersuchung der Lagebeziehung von zwei Ebenen in Parameterform | | ||
Gegeben sind eine Ebene <math>E: \vec{x}=\left( \begin{matrix} 1\\ | Gegeben sind eine Ebene <math>E: \vec{x}=\left( \begin{matrix} 1\\ 4\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} 1\\ -2\\ 1 \end{matrix} \right) + t \cdot \left( \begin{matrix} 3\\ 1\\ -1 \end{matrix} \right) </math> und eine Ebene <math>F: \vec{x}=\left( \begin{matrix} 1\\ 2\\ 3 \end{matrix} \right) + r \cdot \left( \begin{matrix} 2\\ 3\\ -2 \end{matrix} \right)+ u \cdot \left( \begin{matrix} 5\\ 4\\ -3 \end{matrix} \right)</math>. | ||
Untersuche die Lagebeziehung der beiden Ebenen. | Untersuche die Lagebeziehung der beiden Ebenen. | ||
| Zeile 297: | Zeile 297: | ||
'''1. Schritt:''' Setze die beiden Ebenengleichungen gleich. | '''1. Schritt:''' Setze die beiden Ebenengleichungen gleich. | ||
<math>\left( \begin{matrix} 1\\ | <math>\left( \begin{matrix} 1\\ 4\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} 1\\ -2\\ 1 \end{matrix} \right) + t \cdot \left( \begin{matrix} 3\\ 1\\ -1 \end{matrix} \right)= \left( \begin{matrix} 1\\ 2\\ 3 \end{matrix} \right) + r \cdot \left( \begin{matrix} 2\\ 3\\ -2 \end{matrix} \right)+ u \cdot \left( \begin{matrix} 5\\ 4\\ -3 \end{matrix} \right) </math> | ||
'''2. Schritt:''' Stelle das zugehörige lineare Gleichungssystem auf. | '''2. Schritt:''' Stelle das zugehörige lineare Gleichungssystem auf. | ||
<math> \begin{vmatrix} 1 | <math> \begin{vmatrix} 1+k+3l=1+2r+5s \\ 4-2k+l=2+3r+4s \\ k-l=3-2r-3s \end{vmatrix} \Leftrightarrow \begin{vmatrix} -k+3l-2r+5s=0 \\ -2k+l-3r-4s=-2 \\ k-l+2r+3s=3 \end{vmatrix}</math> | ||
'''3. Schritt:''' Löse das Gleichungssystem mit dem Gaußverfahren oder dem Taschenrechner: | '''3. Schritt:''' Löse das Gleichungssystem mit dem Gaußverfahren oder dem Taschenrechner: | ||
<math> \begin{vmatrix} | <math> \begin{vmatrix} 1 & 3 & -2 & 5 & 0 \\ 0 & 7 & -7 & -14 & -2 \\ 0 & 0 & 0 & 0 & -13\end{vmatrix} </math> | ||
'''4. Schritt:''' Interpretiere die Lösung des Gleichungssystems: | '''4. Schritt:''' Interpretiere die Lösung des Gleichungssystems: | ||
In der dritten Zeile der Lösungsmatrix befindet sich ein Widerspruch. Somit hat das LGS keine Lösunf und die beiden Ebenen sind parallel | |||
| Hervorhebung1}} | | Hervorhebung1}} | ||
| Zeile 346: | Zeile 342: | ||
{{Box | Beispielaufgabe: Untersuchung der Lagebeziehung von zwei Ebenen in Koordinatenform und Parameterform | | {{Box | Beispielaufgabe: Untersuchung der Lagebeziehung von zwei Ebenen in Koordinatenform und Parameterform | | ||
Gegeben sind | Gegeben sind eine Ebene <math>E: \vec{x}=\left( \begin{matrix} 2\\ 1\\ -3 \end{matrix} \right) + r \cdot \left( \begin{matrix} 1\\ 0\\ -11 \end{matrix} \right) + s \cdot \left( \begin{matrix} 2\\ 1\\ 0 \end{matrix} \right) </math> und eine Ebene <math>F: -1{,}5x_1+3x_2-1{,}5x_3=4,5</math>. | ||
''' | '''1. Schritt:''' Prüfe, ob die Richtungsvektoren der Ebene E orthogonal zum Normalenvektor der Ebene E liegen. Hierfür muss das Skalarprodukt der entsprechenden Ve<math> \vec{n} \circ \vec{u}=0</math> und <math> \vec{n} \circ \vec{v}=0</math> | ||
'''3. Schritt:''' | '''3. Schritt:''' | ||
Version vom 8. Mai 2021, 09:52 Uhr
Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
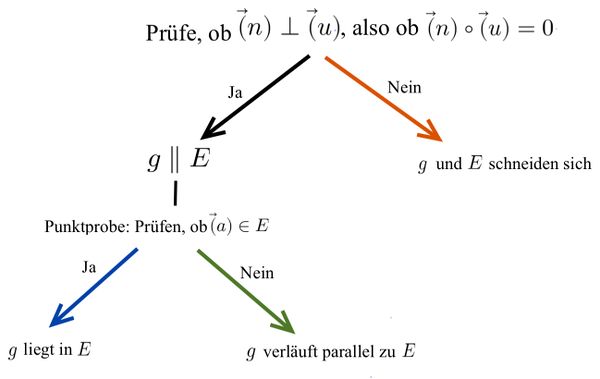
Untersuchung der Lagebeziehung zwischen Gerade und Ebene
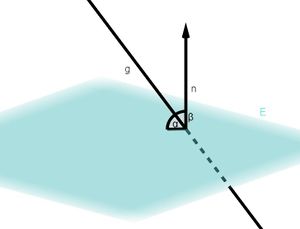
⭐Berechnung des Winkels zwischen Gerade und Ebene
Lagebeziehung Ebene-Ebene
⭐Berechnung des Winkels zwischen Ebene und Ebene