Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 167: | Zeile 167: | ||
Bestimme <math> l </math> und <math> m </math> in den folgenden Geraden so, dass die entsprechende Lagebeziehung erfüllt ist. | Bestimme <math> l </math> und <math> m </math> in den folgenden Geraden so, dass die entsprechende Lagebeziehung erfüllt ist. | ||
a) Die Gerade <math> g: \vec{x} = \left( \begin{matrix} 5\\ 3\\ 0 \end{matrix} \right) + r \cdot \left( \begin{matrix} | a) Die Gerade <math> g: \vec{x} = \left( \begin{matrix} 5\\ 3\\ 0 \end{matrix} \right) + r \cdot \left( \begin{matrix} \frac{1}{2}\\ 3\\ m \end{matrix} \right) </math> soll parallel zur Ebene <math> E </math> verlaufen. | ||
{{Lösung versteckt|1=Damit die Gerade <math>g</math> und die Ebene <math>E</math> parallel zueinander sind, müssen der Richtungsvektor von <math>g</math> und der Normalenvektor von <math>E</math> orthogonal zueinander sein. |2=Tipp anzeigen|3=Tipp verbergen}} | {{Lösung versteckt|1=Damit die Gerade <math>g</math> und die Ebene <math>E</math> parallel zueinander sind, müssen der Richtungsvektor von <math>g</math> und der Normalenvektor von <math>E</math> orthogonal zueinander sein. |2=Tipp anzeigen|3=Tipp verbergen}} | ||
{{Lösung versteckt|1= <math> \vec{u} \ast \vec{n} = \left( \begin{matrix} | {{Lösung versteckt|1= <math> \vec{u} \ast \vec{n} = \left( \begin{matrix} \frac{1}{2}\\ 3\\ m \end{matrix} \right) \ast \left( \begin{matrix} -2\\ 3\\ {-}1 \end{matrix} \right) = 8-m </math>. | ||
Damit die beiden Vektoren orthogonal zueinander sind, muss das Skalarprodukt <math> 0 </math> sein: <math> 8-m = 0 \Rightarrow m = 8 </math>.|2=Lösung anzeigen|3=Lösung verbergen}} | Damit die beiden Vektoren orthogonal zueinander sind, muss das Skalarprodukt <math> 0 </math> sein: <math> 8-m = 0 \Rightarrow m = 8 </math>.|2=Lösung anzeigen|3=Lösung verbergen}} | ||
b) Die Gerade <math> h: \vec{x} = \left( \begin{matrix} | b) Die Gerade <math> h: \vec{x} = \left( \begin{matrix} \frac{51}{10}\\ \frac{2}{5} \end{matrix} \right) + s \cdot \left( \begin{matrix} 3\\ m\\ \frac{18}{5} \end{matrix} \right) </math> soll in der Ebene <math> E </math> liegen. | ||
{{Lösung versteckt|1= Damit die Gerade <math>g</math> in der Ebene <math>E</math> liegt, muss der Richtungsvektor von <math>g</math> und der Normalenvektor von <math>E</math> orthogonal zueinander sein. |2=Tipp 1 anzeigen|3=Tipp 1 verbergen}} | {{Lösung versteckt|1= Damit die Gerade <math>g</math> in der Ebene <math>E</math> liegt, muss der Richtungsvektor von <math>g</math> und der Normalenvektor von <math>E</math> orthogonal zueinander sein. |2=Tipp 1 anzeigen|3=Tipp 1 verbergen}} | ||
{{Lösung versteckt|1= Wenn die Gerade <math>g</math> in der Ebene <math>E</math> liegt, liegt jeder Punkt auf der Gerade <math>g</math> auch in der Ebene <math>E</math>. Prüfe mit der Punktprobe, ob der Stützvektor von <math>g</math> in der Ebene <math>E</math> liegt.|2=Tipp 2 anzeigen|3=Tipp 2 verbergen}} | {{Lösung versteckt|1= Wenn die Gerade <math>g</math> in der Ebene <math>E</math> liegt, liegt jeder Punkt auf der Gerade <math>g</math> auch in der Ebene <math>E</math>. Prüfe mit der Punktprobe, ob der Stützvektor von <math>g</math> in der Ebene <math>E</math> liegt.|2=Tipp 2 anzeigen|3=Tipp 2 verbergen}} | ||
{{Lösung versteckt|1= '''Finde zuerst m:''' <math> \vec{u} \ast \vec{n} = \left( \begin{matrix} 3\\ m\\ | {{Lösung versteckt|1= '''Finde zuerst m:''' <math> \vec{u} \ast \vec{n} = \left( \begin{matrix} 3\\ m\\ \frac{18}{5} \end{matrix} \right) \ast \left( \begin{matrix} -2\\ 3\\ {-}1 \end{matrix} \right) = 3m - \frac{48}{5} </math>. | ||
Damit die beiden Vektoren orthogonal zueinander sind, muss das Skalarprodukt <math> 0 </math> sein: <math> 3m - | Damit die beiden Vektoren orthogonal zueinander sind, muss das Skalarprodukt <math> 0 </math> sein: <math> 3m - \frac{48}{5} = 0 \Rightarrow m = \frac{16}{5} </math>. | ||
'''Finde danach <math>l</math> durch eine Punktprobe:''' Setze <math> \vec(a) = \left( \begin{matrix} l\\ | '''Finde danach <math>l</math> durch eine Punktprobe:''' Setze <math> \vec(a) = \left( \begin{matrix} l\\ \frac{51}{10}\\ \frac{2}{5} \end{matrix} \right) </math> in die Ebenengleichung ein und löse nach l auf: <math> -2l + 3 \cdot \frac{51}{10} - frac{2}{5}= 3 \Leftrightarrow l = \frac{119}{20}</math>. |2=Lösung anzeigen|3=Lösung verbergen}} | ||
c) Die Gerade <math> i: \vec{x} = \left( \begin{matrix} 3\\ 0\\ 2 \end{matrix} \right) + t \cdot \left( \begin{matrix} -3\\ 5\\ {-}1 \end{matrix} \right) </math> soll die Ebene <math> E </math> schneiden. | c) Die Gerade <math> i: \vec{x} = \left( \begin{matrix} 3\\ 0\\ 2 \end{matrix} \right) + t \cdot \left( \begin{matrix} -3\\ 5\\ {-}1 \end{matrix} \right) </math> soll die Ebene <math> E </math> schneiden. | ||
Version vom 8. Mai 2021, 09:45 Uhr
Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".
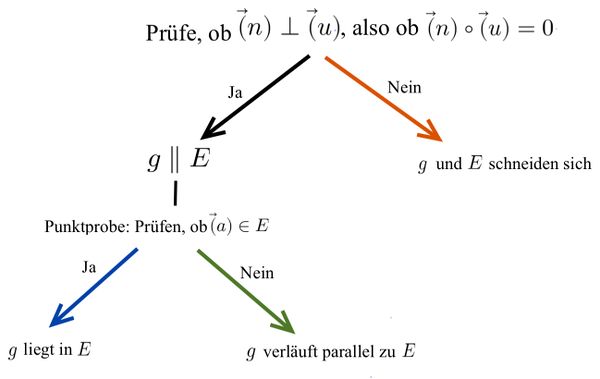
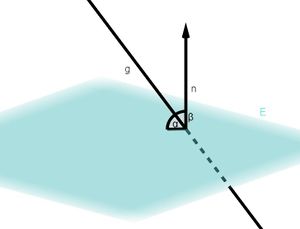
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
Untersuchung der Lagebeziehung zwischen Gerade und Ebene
⭐Berechnung des Winkels zwischen Gerade und Ebene
Lagebeziehung Ebene-Ebene
⭐Berechnung des Winkels zwischen Ebene und Ebene