Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)

Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".

Info

In diesem Lernpfadkapitel <Kurzbeschreibung des Kapitelziels>

Bei den Aufgaben unterscheiden wir folgende Typen:

• In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit.
• Und Aufgaben mit grünem Streifen sind Knobelaufgaben.
• Aufgaben und Kapitel, die mit einem ⭐ gekennzeichnet sind, sind nur für den LK gedacht.

Viel Erfolg!

Lagebeziehung Gerade-Ebene

Mögliche Lagebeziehungen zwischen Gerade und Ebene

Merke:

Zwischen einer Gerade und einer Ebene gibt es drei mögliche Lagebeziehungen.

Die Geraden schneidet die Ebene.

Die Gerade und die Ebene liegen parallel.

Die Gerade liegt in der Ebene.

Untersuchung der Lagebeziehung zwischen Gerade und Ebene

Aufgabe: Lückentext zur Lagebeziehung zwischen Gerade und Ebene

Vorgehen: Die Lagebeziehung einer Gerade und einer Ebene untersuchen.

Beispielaufgabe: Untersuchung der Lagebeziehung von Gerade und Ebene

Gegeben sind eine Ebene $E: \vec{x}=\left( \begin{matrix} 1\\ 0\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} -1\\ 1\\ 0 \end{matrix} \right) + t \cdot \left( \begin{matrix} -1\\ 0\\ 1 \end{matrix} \right)$ und eine Gerade $g: \vec{x}=\left( \begin{matrix} 2\\ 2\\ 2 \end{matrix} \right) + r \cdot \left( \begin{matrix} -1\\ -4\\ 0 \end{matrix} \right)$. Untersuche die Lagebeziehung der Gerade und der Ebene und bestimme gegebenenfalls den Schnittpunkt.

1. Schritt: Setze die Geraden- und Ebenengleichung gleich: $\left( \begin{matrix} 1\\ 0\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} -1\\ 1\\ 0 \end{matrix} \right) + t \cdot \left( \begin{matrix} -1\\ 0\\ 1 \end{matrix} \right) = \left( \begin{matrix} 2\\ 2\\ 2 \end{matrix} \right) + r \cdot \left( \begin{matrix} -1\\ -4\\ 0 \end{matrix} \right)$

2. Schritt: Stelle das zugehörige lineare Gleichungssystem auf: $\begin{vmatrix} 1-s-t=2-r \\ s=2-4r \\ t=2 \end{vmatrix}$

3. Schritt: Löse das Gleichungssystem mit dem Gaußverfahren oder dem Taschenrechner: $s=-1, t=2, r=1$

4. Schritt: Interpretiere die Lösung des Gleichungssystems anhand der Anzahl der Lösungen. Da das Gleichungssystem nur eine Lösung hat, besitzen die Ebene $E$ und die Gerade $g$ nur einen gemeinsamen Punkt. Also schneidet die Gerade die Ebene.

5. Schritt: Da sich die Ebene $E$ und die Gerade $g$ schneiden, kannst du den Schnittpunkt der beiden berechnen. Setze dafür den Parameter $r$ in die Geradengleichung ein: $\left( \begin{matrix} 2\\ 2\\ 2 \end{matrix} \right) + 1 \cdot \left( \begin{matrix} -1\\ -4\\ 0 \end{matrix} \right) = \left( \begin{matrix} 1\\ -2\\ 2 \end{matrix} \right)$

Aufgabe: Untersuchung der Lagebeziehung zwischen Gerade und Ebene

Gegeben ist eine Ebene $E: \vec{x}=\left( \begin{matrix} 1\\ 0\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} -1\\ 1\\ 0 \end{matrix} \right) + t \cdot \left( \begin{matrix} -1\\ 0\\ 1 \end{matrix} \right)$.

1. Setze die Geradengleichung mit der Ebenengleichung gleich.

2. Stelle ein LGS auf.

3. Löse das LGS mit dem Gaußverfahren oder dem Taschenrechner.

4. Die Anzahl der Lösungen zeigt dir, wie viele gemeinsamen Punkte die Gerade und die Ebene haben. Daran kannst du die Lagebeziehung erkennen.

Aufgabe <Nummer>: Schatten eines Sonnensegels

Da es Frau Meier im Sommer auf ihrer Terrasse gerne schattig haben möchte, spannt sie ein dreieckiges Segeltuch auf. Die Eckpunkte des Segeltuchs sind $A = \left( \begin{matrix} 9\\ -5\\ 7 \end{matrix} \right), B= \left( \begin{matrix} 6\\ -5\\ 7 \end{matrix} \right)$ und $C = \left( \begin{matrix} 7\\ -10\\ 11 \end{matrix} \right)$. Die Terrasse wird modelliert durch die $x_1- x_2$-Ebene. Die Sonne scheint aus Richtung $S = \left( \begin{matrix} -2\\ -2\\ -10 \end{matrix} \right)$. In welchem Bereich hat Frau Meier nun Schatten?

Bestimme die Geraden der Lichtstrahlen durch die Eckpunkte des Sonnensegels und berechne, wo sie auf die Terrasse treffen. Vielleicht hilft dir eine Skizze.

Der Schatten liegt auf der $x_1-x_2$-Ebene und du weißt, dass jeder Punkt auf dieser Ebene von der Form: $P = \left( \begin{matrix} x\\ y\\ 0 \end{matrix} \right)$ ist. Du musst also die Ebenengleichung nicht aufstellen.

1. Schritt: Stelle die Geradengleichungen durch die Eckpunkte des Sonnensegels in Richtung der Sonnenstrahlen auf: $f: \vec{x}=\left( \begin{matrix} 9\\ -5\\ 7 \end{matrix} \right) + r \cdot \left( \begin{matrix} -2\\ -2\\ -10 \end{matrix} \right)$, $g: \vec{x}=\left( \begin{matrix} 6\\ -5\\ 7 \end{matrix} \right) + s \cdot \left( \begin{matrix} -2\\ -2\\ 10 \end{matrix} \right)$, $h: \vec{x}=\left( \begin{matrix} 7\\ -10\\ 11 \end{matrix} \right) + t \cdot \left( \begin{matrix} -2\\ -2\\ 10 \end{matrix} \right)$

2. Schritt: Berechne die Schnittpunkte der Geraden mit der $x_1-x_2$-Ebene. Da du weißt, dass jeder Punkt in dieser Ebene von der Form $P = \left( \begin{matrix} x\\ y\\ 0 \end{matrix} \right)$ ist, kannst du diesen Punkt mit der Geradengleichung gleichsetzen.

Berechnung von $A'$:

$\left( \begin{matrix} x\\ y\\ 0 \end{matrix} \right)=\left( \begin{matrix} 9\\ -5\\ 7 \end{matrix} \right) + r \cdot \left( \begin{matrix} -2\\ -2\\ -10 \end{matrix} \right) \Rightarrow \begin{vmatrix} x=9-2r \\ y=-5-2r \\ 0=7-10r \end{vmatrix} \Rightarrow x=-12,6, y = -6,4, r= 0,7 \Rightarrow A'=\left( \begin{matrix} -12,6\\ -6,4\\ 0 \end{matrix} \right)$.

Berechnung von $B'$:

$\left( \begin{matrix} x\\ y\\ 0 \end{matrix} \right)=\left( \begin{matrix} 6\\ -5\\ 7 \end{matrix} \right) + s \cdot \left( \begin{matrix} -2\\ -2\\ 10 \end{matrix} \right) \Rightarrow \begin{vmatrix} x=6-2s \\ y=-5-2s \\ 0=7-10r \end{vmatrix} \Rightarrow x=-8,4, y = -6,4, r= 0,7 \Rightarrow B'=\left( \begin{matrix} -8,4\\ -6,4\\ 0 \end{matrix} \right)$.

Berechnung von $C'$:

$\left( \begin{matrix} x\\ y\\ 0 \end{matrix} \right)=\left( \begin{matrix} 7\\ -10\\ 11 \end{matrix} \right) + t \cdot \left( \begin{matrix} -2\\ -2\\ 10 \end{matrix} \right) \Rightarrow \begin{vmatrix} x=7-2s \\ y=-10-2s \\ 0=11-10r \end{vmatrix} \Rightarrow x=-15,4, y = -12,2, r= 1,1 \Rightarrow C'=\left( \begin{matrix} -15,4\\ -12,2\\ 0 \end{matrix} \right)$.

Die Schattenfläche wird also durch das Dreieck mit den Eckpunkten $A'=\left( \begin{matrix} -12,6\\ -6,4\\ 0 \end{matrix} \right), B'=\left( \begin{matrix} -8,4\\ -6,4\\ 0 \end{matrix} \right)$ und $C'=\left( \begin{matrix} -15,4\\ -12,2\\ 0 \end{matrix} \right)$ begrenzt.

⭐Merke: Die Lagebeziehung einer Gerade und einer Ebene mit dem Normalenvektor untersuchen

Bei der Bestimmung der Lagebeziehung zwischen einer Gerade $g$ und einer Ebene $E$ kann dir der Normalenvektor der Ebene helfen.

Wenn der Richtungsvektor der Gerade und der Normalenvektor der Ebene orthogonal zueinander sind und Gerade und Ebene keinen gemeinsamen Punkt besitzen, so sind sie parallel zueinander.

Wenn der Richtungsvektor der Gerade und der Normalenvektor der Ebene orthogonal zueinander sind und Gerade und Ebene unendlich viele gemeinsame Punkte besitzen, so liegt die Gerade in der Ebene.

Wenn der Richtungsvektor der Gerade und der Normalenvektor der Ebene nicht orthogonal zueinander sind, dann schneiden sich die Gerade und die Ebene und es kann ein Schnittpunkt bestimmt werden.

⭐Vorgehen: Die Lagebeziehung einer Gerade und einer Ebene untersuchen mit dem Normalenvektor untersuchen

Beispiel: Lagebeziehung einer Gerade und einer Ebene in Koordinatenform

Gegeben sind eine Ebene $E: 2x_1 + x_2 - x_3 = 5$ und eine Gerade $g: \vec{x}=\left( \begin{matrix} 3\\ 0\\ 2 \end{matrix} \right) + r \cdot \left( \begin{matrix} -3\\ 5\\ {-}1 \end{matrix} \right)$. Bestimme die Lagebeziehung von Gerade und Ebene.

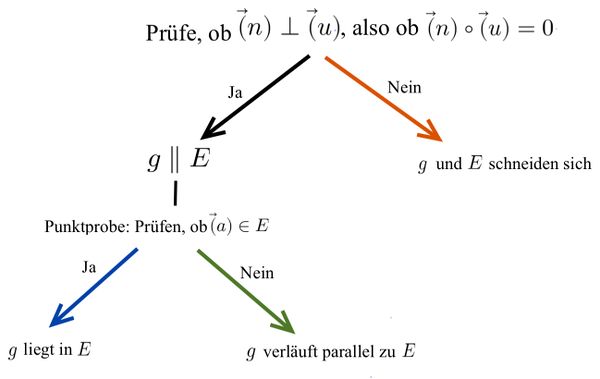
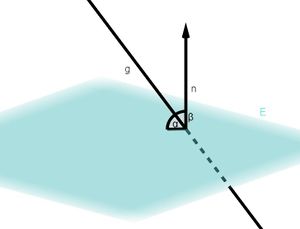
1. Prüfe, ob der Richtungsvektor der Gerade orthogonal zum Normalenvektor der Ebene liegt: $\vec{n} \ast \vec{u} = \left( \begin{matrix} 2\\ 1\\ {-}1 \end{matrix} \right) \circ \left( \begin{matrix} -3\\ 5\\ {-}1 \end{matrix} \right) = 2 \cdot (-3) + 1 \cdot 5 -1 \cdot (-1) = 0$$\Rightarrow \vec{n} \perp \vec{u}$

2. Prüfe durch eine Punktprobe, ob der Stützvektor der Gerade in der Ebene liegt: $2 \cdot 3 -2 =5 \Rightarrow 4 = 5$

$\Rightarrow$ Der Stützvektor liegt nicht in der Ebene. Daher verlaufen die Gerade $g$ und die Ebene $E$ parallel zueinander.

Aufgabe: Bestimme den Parameter

Gegeben ist eine Ebene $E: \vec{x} = -2x_1 + 3x_2 - x_3 = 3$. Bestimme $l$ und $m$ in den folgenden Geraden so, dass die entsprechende Lagebeziehung erfüllt ist.

a) Die Gerade $g: \vec{x} = \left( \begin{matrix} 5\\ 3\\ 0 \end{matrix} \right) + r \cdot \left( \begin{matrix} 0,5\\ 3\\ m \end{matrix} \right)$ soll parallel zur Ebene $E$ verlaufen.

Damit die Gerade $g$ und die Ebene $E$ parallel zueinander sind, müssen der Richtungsvektor von $g$ und der Normalenvektor von $E$ orthogonal zueinander sein.

$\vec{u} \ast \vec{n} = \left( \begin{matrix} 0,5\\ 3\\ m \end{matrix} \right) \circ \left( \begin{matrix} -2\\ 3\\ {-}1 \end{matrix} \right) = 8-m$.

Damit die beiden Vektoren orthogonal zueinander sind, muss das Skalarprodukt $0$ sein: $8-m = 0 \Rightarrow m = 8$.

b) Die Gerade $h: \vec{x} = \left( \begin{matrix} l\\ 5,1\\ 0,4 \end{matrix} \right) + s \cdot \left( \begin{matrix} 3\\ m\\ 3,6 \end{matrix} \right)$ soll in der Ebene $E$ liegen.

Damit die Gerade $g$ in der Ebene $E$ liegt, muss der Richtungsvektor von $g$ und der Normalenvektor von $E$ orthogonal zueinander sein.

Wenn die Gerade $g$ in der Ebene $E$ liegt, liegt jeder Punkt auf der Gerade $g$ auch in der Ebene $E$. Prüfe mit der Punktprobe, ob der Stützvektor von $g$ in der Ebene $E$ liegt.

Finde zuerst m: $\vec{u} \ast \vec{n} = \left( \begin{matrix} 3\\ m\\ 3,6 \end{matrix} \right) \circ \left( \begin{matrix} -2\\ 3\\ {-}1 \end{matrix} \right) = 3m - 9,6$. Damit die beiden Vektoren orthogonal zueinander sind, muss das Skalarprodukt $0$ sein: $3m - 9,6 = 0 \Rightarrow m = 3,2$.

Finde danach $l$ durch eine Punktprobe: Setze $\vec(a) = \left( \begin{matrix} l\\ 5,1\\ 0,4 \end{matrix} \right)$ in die Ebenengleichung ein und löse nach l auf: $-2l + 3 \cdot 5,1 - 0,4 = 3 \Leftrightarrow l = 5,95$.

c) Die Gerade $i: \vec{x} = \left( \begin{matrix} 3\\ 0\\ 2 \end{matrix} \right) + t \cdot \left( \begin{matrix} -3\\ 5\\ {-}1 \end{matrix} \right)$ soll die Ebene $E$ schneiden.

Es gibt keine eindeutige Lösung! Der Richtungsvektor $\vec{u}$ von $g$ darf nur nicht orthogonal zum Normalenvektor von $E$ liegen.

Für $m = 3$ ist der Richtungsvektor von $g$ orthogonal zum Normalenvektor von $E$ und die Gerade $g$ liegt parallel zur Ebene $E$. Jeder andere Wert für $m$ ist eine richtige Lösung.

Aufgabe <Nummer>: Beamer

Luca hält einen Vortrag vor seiner Klasse. Mit einem Laserpointer möchte er auf einer Karte an der Wand etwas zeigen. Die Wand des Klassenraums wird durch die Ebene $E: x_2 + 3x_3 = 2$ dargestellt. Der Strahl des Laserpointes wird durch die Gerade $j: \vec{x} = \left( \begin{matrix} {-}5\\ 1,5 \end{matrix} \right) + s \cdot \left( \begin{matrix} 1\\ 2\\ 0,5 \end{matrix} \right)$ modelliert. Berechne ohne Taschenrechner, wo der Strahl aus Lucas Laserpointer auf die Karte an der Wand trifft.

Berechne den Schnittpunkt der Gerade mit der Ebene, indem die die einzelnen Koordinaten der Gerade in die Ebenengleichung einsetzt.

$-5 + 2s + 3(1,5 + 0,5s) = 2 \Leftrightarrow s \approx 0,71$

Berechne den Schnittpunkt, indem du s in die Geradengleichung einsetzt: $\left( \begin{matrix} 7\\ {-}5\\ 1,5 \end{matrix} \right) + 0,71 \cdot \left( \begin{matrix} 1\\ 2\\ 0,5 \end{matrix} \right) \approx \left( \begin{matrix} 7,71\\ -3,58\\ 1,86 \end{matrix} \right)$

⭐Berechnung des Winkels zwischen Gerade und Ebene

Abbildung: Winkel zwischen Gerade und Ebene

Erläuterung: Winkel berechnen zwischen Gerade und Ebene

Wenn eine Gerade g eine Eben E schneidet, kannst du nicht nur den Schnittpunkt berechnen, sondern auch den Schnittwinkel. Dafür benötigen wir den Normalenvektor. Wenn du nicht mehr genau weißt, wie man diesen abliest oder berechnet, schau noch einmal in Kapitel...

Merksatz: Winkel berechnen zwischen Gerade und Ebene

Sei $E$ eine Ebene mit dem Normalenvektor $n$ und $g$ eine Gerade mit dem Richtungsvektor $u$. Der Schnittwinkel $\beta$ zwischen $E$ und $g$ kann mit folgender Formel berechnet werden: $sin(\beta)=\frac{ n \ast u}{|n| \cdot |u|}$

Wenn du wissen möchtest, warum du nicht wie beim Winkel zwischen zwei Geraden den Kosinus benutzt, kannst du das hier nachlesen:

Der Normalenvektor $\vec{n}$ einer Ebene steht in einem 90 Winkel zur Ebene $E$. Wenn wir den Winkel zwischen einer Gerade $g$ und einer $E$ berechnen wollen, können wir wie beim Winkel zwischen zwei Geraden mit der Kosinusfunktion den Winkel zwischen dem Richtungsvektor von $g$ und dem Normalenvektor von $E$ berechnen. In Abbildung ... ist dieser Winkel mit $\beta$ bezeichnet. Um nun den Winkel $\alpha$ zwischen $g$ und $E$ zu erhalten, müssen wir $\beta$ von $90 ^\circ$ abziehen. Dies entspricht der obigen Formel mit der Sinusfunktion.

Beispiel: Berechnen des Winkels zwischen Gerade und Ebene

Gegeben sind die Gerade $g: \vec{x}=\left( \begin{matrix} -1\\ 3\\ 6 \end{matrix} \right) + r \cdot \left( \begin{matrix} 8\\ 2\\ 0 \end{matrix} \right)$ und die Ebene $E: 2x_1 + x_2 + 4 x_3 = -27$. Bestimme den Winkel unter dem sich die Gerade $g$ und die Ebene $E$ schneiden.

1. Schritt: Notiere den Richtungvektor $\vec{u}$ der Gerade und den Normalenvektor $\vec{n}$ der Ebene.

$\vec{u}= \left( \begin{matrix} 8\\ 2\\ 0 \end{matrix} \right)$ und $\vec{n}= \left( \begin{matrix} 2\\ 1\\ 4 \end{matrix} \right)$.

2. Schritt: Setze die Vektoren in die Formel $sin(\beta)=\frac{ \vec{n} \ast \vec{u}}{|\vec{n}| \cdot |\vec{u}|}$ ein. $sin(\beta)=\frac{ | \left( \begin{matrix} 2\\ 1\\ 4 \end{matrix} \right) \ast \left( \begin{matrix} 8\\ 2\\ 0 \end{matrix} \right)|}{|\left( \begin{matrix} 2\\ 1\\ 4 \end{matrix} \right)| \cdot | \left( \begin{matrix} 8\\ 2\\ 0 \end{matrix} \right)|} \Leftrightarrow sin(\beta)=\frac{18}{\sqrt{60} \cdot \sqrt{21}} \Leftrightarrow sin(\beta)=\frac{18}{\sqrt{1260}}$

3. Schritt: Umformen der Gleichung

$\beta = sin^{-1}(\frac{18}{\sqrt{1260}}) \Leftrightarrow \beta \approx 28,45 ^\circ$

Aufgabe <Nummer>: <Name>

Inhalt

Aufgabe <Nummer>: Gerade gesucht

Eine Gerade $g$ soll die $x_1-x_2-Ebene$ in einem Winkel von $45 ^\circ$ schneiden. Über die Gerade $g$ ist nur bekannt, dass sie im Punkt $P (1|2|3)$ beginnt und sie in Richtung des Vektors $\vec{x}=\begin{pmatrix} 3\\ 6\\ z \end{pmatrix}$ verläuft. Stelle die Gerade $g$ auf.

Notiere dir alle Informationen aus dem Text. Was weißt du über die Berechnung des Winkels zwischen einer Gerade und einer Ebene?

Der Normalenvektor der $x_1-x_2$ -Ebene verläuft nur in $x_3$-Richtung.

Um Gleichungen mit einer Unbekannten zu lösen, kannst du die nSolve-Funktion deines Taschenrechners nutzen.

Bisher wurde mit der Formel zu Winkelberechnung nur der Winkel berechnet. Die Formel kann jedoch auch genutzt werden, um bei einem vorgegebenen Winkel die Lage der Gerade oder Ebene zu bestimmen.

Dafür muss zuerst der Normalenvektor der Ebene bestimmt werden. Da es sich um die $x_1-x_2$ -Ebene handelt, lautet der Normalenvektor $\vec{n}=\begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix}$.

Nun können der Normalenvektor der Ebene, der Richtungsvektor der Gerade und der vorgegebene Winkel in die Formel zur Berechnung eingesetzt werden: $sin(45)=\frac{ \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix} \ast \begin{pmatrix} 3\\ 6\\ z \end{pmatrix}}{\begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix} \cdot \begin{pmatrix} 3\\ 6\\ z \end{pmatrix}} \Leftrightarrow sin(45)=\frac{z}{\sqrt{1} \cdot \sqrt{9+36 + z^{2}}} \Leftrightarrow sin(45)=\frac{z}{\sqrt{45+z^{2}}}$

Löst man die Gleichung mithilfe des Taschenrechners, erhält man das Ergebnis: $z=3 \sqrt{5} \approx 6,71$.

Somit kann im letzten Schritt die Gerade $g$ aufgestellt werden. Man erhält $g: \vec{x} = \left( \begin{matrix} 1\\ 2\\ 3 \end{matrix} \right) + r \cdot \left( \begin{matrix} 3\\ 6\\ {3 \sqrt{5}} \end{matrix} \right)$.

Lagebeziehung Ebene-Ebene

Merke:

Zwischen einer Gerade und einer Ebene gibt es drei mögliche Lagebeziehungen.

Die Ebenen schneiden sich in einer Schnittgeraden.

Die Ebenen sind parallel.

Die Ebene sind identisch.

Aufgabe: Lückentext zur Lagebeziehung zwischen Ebene und Ebene

Merke: Lagebeziehung von zwei Ebenen in Parameterform untersuchen.

Beispielaufgabe: Untersuchung der Lagebeziehung von zwei Ebenen in Parameterform

Gegeben sind eine Ebene $E: \vec{x}=\left( \begin{matrix} 1\\ 2\\ 3 \end{matrix} \right) + s \cdot \left( \begin{matrix} -1\\ 2\\ 3 \end{matrix} \right) + t \cdot \left( \begin{matrix} 1\\ 1\\ 1 \end{matrix} \right)$ und eine Ebene $F: \vec{x}=\left( \begin{matrix} 2\\ 0\\ 3 \end{matrix} \right) + r \cdot \left( \begin{matrix} -1\\ 2\\ 1 \end{matrix} \right)+ u \cdot \left( \begin{matrix} -1\\ 1\\ 1 \end{matrix} \right)$. Untersuche die Lagebeziehung der beiden Ebenen.

1. Schritt: Setze die beiden Ebenengleichungen gleich. $\left( \begin{matrix} 1\\ 2\\ 3 \end{matrix} \right) + s \cdot \left( \begin{matrix} -1\\ 2\\ 3 \end{matrix} \right) + t \cdot \left( \begin{matrix} 1\\ 1\\ 1 \end{matrix} \right)= \left( \begin{matrix} 2\\ 0\\ 3 \end{matrix} \right) + r \cdot \left( \begin{matrix} -1\\ 2\\ 1 \end{matrix} \right)+ u \cdot \left( \begin{matrix} -1\\ 1\\ 1 \end{matrix} \right)$

2. Schritt: Stelle das zugehörige lineare Gleichungssystem auf. $\begin{vmatrix} 1-1k+l=2-r-s \\ 2+2k+l=2r+s \\ 3+3k+l=3+r+s \end{vmatrix} \Leftrightarrow \begin{vmatrix} -k+l+r+s=1 \\ 2k+l-2r-s=-2 \\ 3k+l-r-s=0 \end{vmatrix}$

3. Schritt: Löse das Gleichungssystem mit dem Gaußverfahren oder dem Taschenrechner: $\begin{vmatrix} -1 & 1 & 1 & 1 & 1 \\ 0 & 3 & 0 & 1 & 1 \\ 0 & 0 & 6 & 2 & 9\end{vmatrix}$

4. Schritt: Interpretiere die Lösung des Gleichungssystems: Aus der dritten Zeile folgt, dass $r=\left ( \frac{3}{2} \right )-\left( \frac{1}{3} \right )s$.

5. Schritt: Bestimme die Schnittgerade der beiden Ebenen. Setze dazu den Parameter $r$ in die Ebenengleichung von $F$ ein. Somit erhälst du die Schnittgerade $g: \vec{x} = \left( \begin{matrix} 0{,}5\\ 3\\ 4{,}5 \end{matrix} \right) + s \cdot \left( \begin{matrix} -\left( \frac{2}{3} \right )\\ -\left( \frac{1}{3} \right )\\ \left( \frac{2}{3} \right )\end{matrix} \right)$

Aufgabe: Ergebnisse interpretieren

Interpretiere die jeweilige Situation geometrisch.

a)  $\begin{vmatrix} 1 & 0 & 0 & -0,5 & 0,5 \\ 0 & 1 & 0 & -1 & 0,5 \\ 0 & 0 & 1 & 1,5 & 1 \end{vmatrix}$

Das Gleichungssystem besitzt unendlich viele Lösungen. Da sich in jeder Zeile der Diagonalform Einträge befinden, schneiden sich die Ebenen in einer Schnittgeraden.

b)  $\begin{vmatrix} 1 & 3 & -2 & 5 & 0 \\ 0 & 7 & -7 & -14 & -2 \\ 0 & 0 & 0 & 0 & -13 \end{vmatrix}$

Das Gleichungssystem besitzt keine Lösung, da die dritte Zeile nicht lösbar ist. Die Ebenen liegen also parallel zueinander.

c)  $\begin{vmatrix} 1 & 3 & -2 & -5 & 3 \\ 0 & 7 & -7 & 14 & 7 \\ 0 & 0 & 0 & 0 & 0 \end{vmatrix}$

Das Gleichungssystem besitzt unendlich viele Lösungen. Da die dritte Zeile nur aus Nullen besteht, sind zwei Parameter frei wählbar und die Ebenen identisch.

Merke: Lagebeziehung von zwei Ebenen in Koordinatenform und Parameterform untersuchen.

Beispielaufgabe: Untersuchung der Lagebeziehung von zwei Ebenen in Koordinatenform und Parameterform

Gegeben sind

1. Schritt:

2. Schritt:

3. Schritt:

4. Schritt:

5. Schritt:

Aufgabe: Lagebeziehungen berechnen

Untersuche die Lagebeziehung der jeweiligen Ebenen.

a) $E: \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 2{,}5 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 0 \\ -2 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 1 \\ -1{,}5 \end{pmatrix}, t,s \in \mathbb{R}$

b) $E: \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 2{,}5 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 0 \\ -2 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 1 \\ -1{,}5 \end{pmatrix}, t,s \in \mathbb{R}$

c)  $E: \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 2{,}5 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 0 \\ -2 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 1 \\ -1{,}5 \end{pmatrix}, t,s \in \mathbb{R}$

Merke: Lagebeziehung von zwei Ebenen in Koordinatenform untersuchen.

Beispielaufgabe: Untersuchung der Lagebeziehung von zwei Ebenen in Koordinatenform

Gegeben sind

1. Schritt:

2. Schritt:

3. Schritt:

4. Schritt:

5. Schritt:

Aufgabe: Untersuchung der Lagebeziehung zwischen zwei Ebenen in Koordinatenform

Gegeben ist eine Ebene $E: \vec{x}=-2x_1-3x_2+x_3=2$.

Aufgabe: Schnitt von zwei Zeltflächen

Die beiden Seitenflächen eines Zeltes liegen in den Ebenen $E: \vec{x} = \begin{pmatrix} 8 \\ 0 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 3 \\ 4\end{pmatrix}, r,s \in \mathbb{R}$ und $E: \vec{x} = \begin{pmatrix} 8 \\ 6 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix}+ u \cdot \begin{pmatrix} 0 \\ -3 \\ 4 \end{pmatrix}, t,u \in \mathbb{R}$. Berechne die Geradengleichung der oberen Zeltkante.

⭐Berechnung des Winkels zwischen Ebene und Ebene

Merke: Winkel berechnen zwischen zwei Ebenen

Wenn sich zwei Ebenen schneiden, kann der Schnittwinkel bestimmt werden, den sie einschließen. Wie in Abbildung ... zu sehen ist, kannst du dazu die Normalenvektoren betrachten. Sie schließen denselben Winkel ein, wie die beiden Ebenen. Betrachten wir die Normalenvektoren, so können wir ähnlich vorgehen, wie beim Berechnen des Winkels zwischen zwei Geraden.

Um den Schnittwinkel zu berechnen, musst du zunächst die Normalenvektoren der Ebenen bestimmen. Wenn du nicht mehr genau weißt, wie das geht, schaue nochmal in Kapitel Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum

Merksatz: <Name>

Seien $E$ und $F$ zwei sich schneidende Ebenen mit den Normalenvektoren $n$ und $m$. Der Schnittwinkel $\alpha$ zwischen $E$ und $F$ kann mit folgender Formel berechnet werden: $cos(\alpha)=\frac{ \vec{n} \ast \vec{m}}{|\vec{n}| \cdot |\vec{m}|}$

Beispiel: Winkel berechnen zwischen zwei Ebenen

Gegeben sind zwei Ebenen $E$ und $F$ mit $E: \vec{x} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ 3 \\ -6 \end{pmatrix}+ s \cdot \begin{pmatrix} 1 \\ 1 \\ 0\end{pmatrix}, r,s \in \mathbb{R}$ und $F: 7x_1+x_2-3x_3$. Berechne den Schnittpunkt zwischen den Ebenen.

1. Schritt: Bestimmte die Normalenvektoren von $E$ und $F$.

Der Normalenvektor von $E$ kann mithilfe des ... bestimmt werden als $\vec{n} = \begin{pmatrix} 2 \\ -2 \\ -1 \end{pmatrix}$ . Der Normalenvektor von $F$ lautet $\vec{m} = \begin{pmatrix} 7 \\ 1 \\ -3 \end{pmatrix}$.

2. Schritt: Einsetzen der Normalenvektoren in die Formel.

$cos(\alpha) = \frac{ \begin{pmatrix} 2 \\ -2 \\ -1 \end{pmatrix} \ast \begin{pmatrix} 7 \\ 1 \\ -3 \end{pmatrix}}{\begin{pmatrix} 2 \\ -2 \\ -1 \end{pmatrix} \cdot \begin{pmatrix} 7 \\ 1 \\ -3 \end{pmatrix}} \Leftrightarrow cos(\alpha) = \frac{59}{\sqrt{9} \cdot \sqrt{59}} \Leftrightarrow cos(\alpha) = \frac{16}{3 \cdot \sqrt{59}}$

3. Schritt: Auflösen der Gleichung.

$\alpha = cos^{-1}(\frac{16}{3 \cdot \sqrt {59}}) \Leftrightarrow \alpha \approx 46{,}03 ^{\circ}$ Der Winkel zwischen den Ebenen $E$ und $F$ beträgt ca. $46{,}03 ^{\circ}$.

Aufgabe <Nummer>: Fehlerbeschreibung

Inhalt

Aufgabe <Nummer>: Bank am Wanderweg

An einem Wanderweg soll eine Holzbank aufgestellt werden. Die Bank wird so ausgerichtet, dass die Sitzfläche durch die Ebene $S_1: \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 0{,}5 \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ 0 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 2 \\ 0{,}4 \\ 0\end{pmatrix}, r,s \in \mathbb{R}$ und die Rückenlehne durch die Ebene $R_1: -x_2 + 0{,}4 x_3 = -0{,}2$ beschrieben werden kann.

Skizze: Bank am Wanderweg

a) Um eine bequeme Sitzposition zu ermöglichen, sollte der Winkel zwischen Rückenlehne und Sitzfläche zwischen 100 und 110 liegen. Überprüfe, ob die auf die neue Bank zutrifft.

Berechne zunächst den Normalenvektor der Ebene $S-1$ aus den Richtungsvektoren der Ebene. Wenn du nicht mehr genau weißt, wie das geht, schaue in Kapitel Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum. 

Überlege genau, welchen Winkel du berechnet hast. Vielleicht kann dir eine Skizze helfen.

Als Normalenvektor der Ebene $S_1$ erhält man $\vec{n}=\begin{pmatrix} 0 \\ 0 \\ 0{,}8 \end{pmatrix}$ und als Normalenvektor der Ebene $R_1$ $\vec{m}=\begin{pmatrix} 0 \\ -1 \\ 0{,}4 \end{pmatrix}$ .

Einsetzen in die Formel liefert: $cos(\gamma) = \frac{ \begin{pmatrix} 0 \\ 0 \\ 0{,}8 \end{pmatrix} \ast \begin{pmatrix} 0 \\ -1 \\ 0{,}4 \end{pmatrix}}{\begin{pmatrix} 0 \\ 0 \\ 0{,}8 \end{pmatrix} \cdot \begin{pmatrix} 0 \\ -1 \\ 0{,}4 \end{pmatrix}} \Leftrightarrow cos(\gamma) = \frac{\frac{8}{25}}{\frac{4}{5} \cdot \sqrt{\frac{29}{25}}}$

Umstellen der Formel ergibt: $\gamma=cos^{-1} \left( \frac{\frac{8}{25}}{\frac{4}{5} \cdot \sqrt{\frac{29}{25}}} \right) \Leftrightarrow \gamma \approx 68{,}2 ^\circ$

Skizze: Winkel zwischen der Rückenlehne und der Sitzfläche der Bank

Wie in Abbildung ... zu sehen wurde der Winkel $\gamma$ berechnet. Der Winkel zwischen der Sitzfläche und der Rückenlehne wird aber durch den Winkel $\alpha$ beschrieben. $\alpha$ erhält man, indem man $180 ^\circ - \gamma$ berechnet: $180 ^\circ - 68{,}2 ^\circ = 111{,}8 ^\circ$. Mit einem Wert von  $111{,}8 ^\circ$ liegt der Winkel zwischen Rückenlehne und Sitzfläche etwas über dem optimalen Winkel.

b) Da der Wanderweg sehr beliebt ist, soll noch eine zweite Bank aufgestellt werden. Sie wird so ausgerichtet, dass beide Bänke mit den Rückenlehnen aneinander stehen. Auch bei der zweiten Bank können die Sitzfläche und die Rückenlehne durch Ebenen beschrieben werden. Die Sitzfläche entspricht der Ebene $S_2: \vec{x} = \begin{pmatrix} 0 \\ 0,8 \\ 0,5 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ 0,4 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 2 \\ 0 \\ 0\end{pmatrix}, r,s \in \mathbb{R}$ und die Rückenlehne der Ebene $R_2: -x_2 - 0{,}4 x_3 = -1$ Berechne den Winkel, unter dem die beiden Rückenlehnen der Bänke aufeinander treffen.

Skizze: Bänke am Wanderweg

Gesucht ist der Winkel zwischen der Ebene $R_1$ und der Ebene $R_2$. Nutze zur Berechnung die Normalenvektoren der Ebenen.

Es soll der Winkel zwischen den beiden Rückenlehnen $R_1$ und $R_2$ berechnet werden.

Skizze: Winkel zwischen den beiden Bänken am Wanderweg

Die Normalenvektoren der Ebenen lauten $\vec{m}=\begin{pmatrix} 0 \\ -1 \\ 0{,}4 \end{pmatrix}$ und $\vec{l}=\begin{pmatrix} 0 \\ -1 \\ -0{,}4 \end{pmatrix}$.

Einsetzen in die Formel liefert:

$cos(\beta)=\frac{ \begin{pmatrix} 0\\ -1\\ 0{,}4 \end{pmatrix} \ast \begin{pmatrix} 0\\ -1\\ -0{,}4 \end{pmatrix}}{\begin{pmatrix} 0\\ -1\\ 0{,}4 \end{pmatrix} \cdot \begin{pmatrix} 0\\ -1\\ -0{,}4 \end{pmatrix}}$

$\Leftrightarrow cos(\beta)=\frac{\frac{21}{25}}{\sqrt{\frac{29}{25}} \cdot \sqrt{\frac{29}{25}}} \Leftrightarrow cos(\beta)=\frac{\frac{21}{25}}{\frac{29}{25}} \Leftrightarrow cos(\beta)=\frac{21}{29}$

Umstellen der Formel ergibt: $\beta=cos^{-1} \left( \frac{21}{29} \right) \Leftrightarrow \beta \approx 43{,}6 ^{\circ}$. Der Winkel zwischen den beiden Rückenlehnen beträgt $43{,}6 ^{\circ}$.