Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 76: | Zeile 76: | ||
{{Lösung versteckt|1= '''1. Schritt:''' |2= Lösung anzeigen| 3= Lösung verbergen}} | {{Lösung versteckt|1= '''1. Schritt:''' |2= Lösung anzeigen| 3= Lösung verbergen}} | ||
Hervorhebung1}} | <nowiki>Hervorhebung1}}</nowiki> | ||
{{Box| Aufgabe: Bestimme den Parameter | | {{Box| Aufgabe: Bestimme den Parameter | | ||
| Zeile 147: | Zeile 147: | ||
{{Box | Aufgabe <Nummer>: <Name> | Inhalt | Arbeitsmethode}} | {{Box | Aufgabe <Nummer>: <Name> | Inhalt | Arbeitsmethode}} | ||
{{Box | Aufgabe <Nummer>: Gerade gesucht | | |||
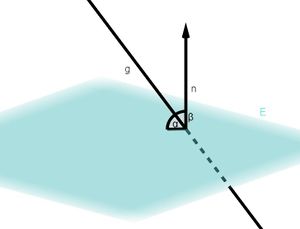
Eine Gerade <math>g</math> soll die <math>x_1-x_2-Ebene </math> in einem Winkel von <math>45 ^\circ</math> schneiden. Über die Gerade <math>g</math> ist nur bekannt, dass sie im Punkt <math>P (1|2|3) </math> beginnt und sie in Richtung des Vektors <math>\vec{x}=\begin{pmatrix} 3\\ 6\\ z \end{pmatrix}</math> verläuft. Stelle die Gerade <math>g</math> auf. | Eine Gerade <math>g</math> soll die <math>x_1-x_2-Ebene </math> in einem Winkel von <math>45 ^\circ</math> schneiden. Über die Gerade <math>g</math> ist nur bekannt, dass sie im Punkt <math>P (1|2|3) </math> beginnt und sie in Richtung des Vektors <math>\vec{x}=\begin{pmatrix} 3\\ 6\\ z \end{pmatrix}</math> verläuft. Stelle die Gerade <math>g</math> auf. | ||
| Zeile 155: | Zeile 155: | ||
{{Lösung versteckt|1=Inhalt|2=Tipp 2 anzeigen|3=Tipp 2 verbergen}} | {{Lösung versteckt|1=Inhalt|2=Tipp 2 anzeigen|3=Tipp 2 verbergen}} | ||
{{Lösung versteckt|1= Arbeitsmethode}} | {{Lösung versteckt|1=Bisher wurde mit der Formel zu Winkelberechnung nur der Winkel berechnet. Die Formel kann jedoch auch genutzt werden, um bei einem vorgegebenen Winkel die Lage der Gerade oder Ebene zu bestimmen. | ||
Dafür muss zuerst der Normalenvektor der Ebene bestimmt werden. Da es sich um die <math>x_1-x_2</math> -Ebene handelt, lautet der Normalenvektor <math>\vec{n}=\begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix}</math>. | |||
Nun können der Normalenvektor der Ebene, der Richtungsvektor der Gerade und der vorgegebene Winkel in die Formel zur Berechnung eingesetzt werden: <math> sin(\alpha)=\frac{ \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix} \ast \begin{pmatrix} 3\\ 6\\ z \end{pmatrix}}{\begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix} \cdot \begin{pmatrix} 3\\ 6\\ z \end{pmatrix}} \Leftrightarrow sin(\beta)=\frac{z}{\sqrt{1} \cdot \sqrt{45 + z^{2}}} \Leftrightarrow sin(\beta)=\frac{z}{\sqrt{45+z^{2}}} </math> | |||
Löst man die Gleichung mithilfe des Taschenrechners, erhält man das Ergebnis: <math> z = 3 \cdot \sqrt{5} \approx 6,71 </math>. | |||
Somit kann im letzten Schritt die Gerade <math>g</math> aufgestellt werden. Man erhält <math>g: \vec{x}= /begin{pmatrix} 1\\ 2\\ 3 \end{pmatrix} + r \cdot /begin{pmatrix} 3\\ 6\\ 3 \cdot \sqrt{5} \end{pmatrix} </math> |2=Lösung anzeigen|3=Lösung verbergen}} | |||
| Arbeitsmethode}} | |||
==Lagebeziehung Ebene-Ebene== | ==Lagebeziehung Ebene-Ebene== | ||
Version vom 7. Mai 2021, 09:20 Uhr
Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
{{Box | Aufgabe <Nummer>: Schatten eines Sonnensegels | Da es Frau Meier im Sommer auf ihrer Terrasse gerne schattig haben möchte, spannt sie ein dreieckiges Segeltuch auf. Die Eckpunkte des Segeltuchs sind und . Die Terrasse wird modelliert durch die -Ebene. Die Sonne scheint aus Richtung . In welchem Bereich hat Frau Meier nun Schatten?
Bestimme die Geraden der Lichtstrahlen durch die Eckpunkte des Sonnensegels und berechne, wo sie auf die Terrasse treffen. Vielleicht hilft dir eine Skizze.
Der Schatten liegt auf der -Ebene und du weißt, dass jeder Punkt auf dieser Ebene von der Form: ist. Du musst also die Ebenengleichung nicht aufstellen.
1. Schritt:
Hervorhebung1}}
⭐Berechnung des Winkels zwischen Gerade und Ebene
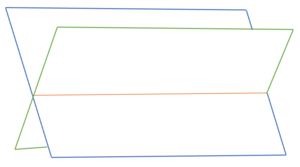
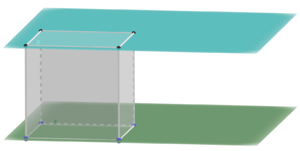
Lagebeziehung Ebene-Ebene
⭐Berechnung des Winkels zwischen Ebene und Ebene