Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung |
Marie (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 170: | Zeile 170: | ||
==Lagebeziehung Ebene-Ebene== | ==Lagebeziehung Ebene-Ebene== | ||
| Zeile 187: | Zeile 184: | ||
{{Box|Untersuchung der Lagebeziehung | {{Box | Beispielaufgabe: Untersuchung der Lagebeziehung von zwei Ebenen | | ||
Gegeben sind eine Ebene <math>E: \vec{x}=\left( \begin{matrix} 2\\ 3\\ 2 \end{matrix} \right) + s \cdot \left( \begin{matrix} -3\\ 1\\ 1 \end{matrix} \right) + t \cdot \left( \begin{matrix} 1\\ -1\\ 1 \end{matrix} \right) </math> und eine Ebene <math>F: \vec{x}=\left( \begin{matrix} 2\\ 2\\ 2 \end{matrix} \right) + r \cdot \left( \begin{matrix} -1\\ 1\\ 1 \end{matrix} \right)+ u \cdot \left( \begin{matrix} -2\\ 1\\ 3 \end{matrix} \right) </math>. Untersuche die Lagebeziehung der beiden Ebenen. | |||
'''1. Schritt:''' Setze die beiden Ebenengleichungen gleich. <math>\left( \begin{matrix} 2\\ 3\\ 2 \end{matrix} \right) + s \cdot \left( \begin{matrix} -3\\ 1\\ 1 \end{matrix} \right) + t \cdot \left( \begin{matrix} 1\\ -1\\ 1 \end{matrix} \right) = \left( \begin{matrix} 2\\ 2\\ 2 \end{matrix} \right) + r \cdot \left( \begin{matrix} -1\\ 1\\ 1 \end{matrix} \right)+ u \cdot \left( \begin{matrix} -2\\ 1\\ 3 \end{matrix} \right) </math> | |||
'''2. Schritt:''' Stelle das zugehörige lineare Gleichungssystem auf. <math> \begin{vmatrix} 2-3s+t=2-r-2u \\ 3+s-t=2+r+u \\ 2+s+t=2+r+3u \end{vmatrix} </math> | |||
| Hervorhebung1}} | | Hervorhebung1}} | ||
| Zeile 216: | Zeile 207: | ||
a) <math>\begin{vmatrix} 1 & 0 & 0 & -0,5 & 0,5 \\ 0 & 1 & 0 & -1 & 0,5 \\ 0 & 0 & 1 & 1,5 & 1 \end{vmatrix}</math> | a) <math>\begin{vmatrix} 1 & 0 & 0 & -0,5 & 0,5 \\ 0 & 1 & 0 & -1 & 0,5 \\ 0 & 0 & 1 & 1,5 & 1 \end{vmatrix}</math> | ||
{{Lösung versteckt|1=Das Gleichungssystem besitzt unendlich viele Lösungen. Da sich in jeder Zeile der Diagonalform Einträge befinden, schneiden sich die Ebenen in einer Schnittgeraden.|2=Lösung anzeigen|3=Lösung verbergen}} | |||
b) <math>\begin{vmatrix} 1 & 0 & -1 & -2 & 0 \\ 0 & 1 & -1 & -3 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{vmatrix}</math> | b) <math>\begin{vmatrix} 1 & 0 & -1 & -2 & 0 \\ 0 & 1 & -1 & -3 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{vmatrix}</math> | ||
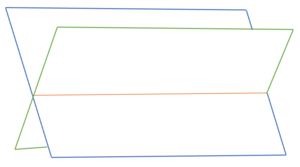
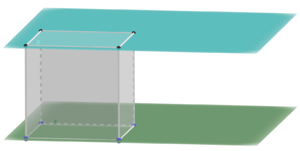
{{Lösung versteckt|1=Das Gleichungssystem besitzt keine Lösung. Die Ebenen liegen also parallel zueinander.|2=Lösung anzeigen|3=Lösung verbergen}} | |||
c) <math>\begin{vmatrix} 1 & 0 & -1 & -2 & 1 \\ 0 & 1 & -1 & -3 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{vmatrix}</math> | c) <math>\begin{vmatrix} 1 & 0 & -1 & -2 & 1 \\ 0 & 1 & -1 & -3 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{vmatrix}</math> | ||
{{Lösung versteckt|1=Das Gleichungssystem besitzt unendlich viele Lösungen. Da die letzte Zeile der Diagonalform nur aus Nullen besteht, sind die Ebenen identisch.|2=Lösung anzeigen|3=Lösung verbergen}} | |||
|Arbeitsmethode}} | |Arbeitsmethode}} | ||
| Zeile 251: | Zeile 244: | ||
|Arbeitsmethode}} | |Arbeitsmethode}} | ||
===⭐Berechnung des Winkels zwischen Ebene und Ebene=== | ===⭐Berechnung des Winkels zwischen Ebene und Ebene=== | ||
Version vom 6. Mai 2021, 23:25 Uhr
Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".
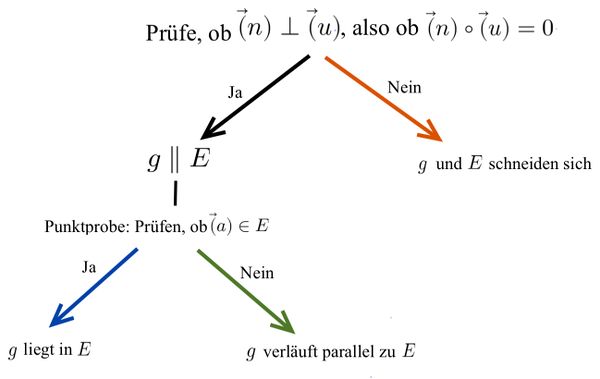
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
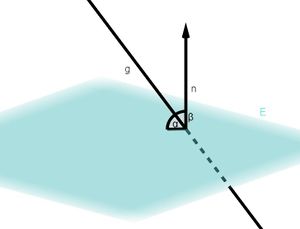
⭐Berechnung des Winkels zwischen Gerade und Ebene
{{Box | Aufgabe <Nummer>: Gerade gesucht |
Eine Gerade soll die in einem Winkel von schneiden. Über die Gerade ist nur bekannt, dass sie im Punkt beginnt und sie in Richtung des Vektors verläuft. Stelle die Gerade auf.
Inhalt
Inhalt
Arbeitsmethode
Lagebeziehung Ebene-Ebene
⭐Berechnung des Winkels zwischen Ebene und Ebene