Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 289: | Zeile 289: | ||
<math> cos(\beta)=\frac{ | \begin{matrix} 0\\ -1\\ 0{,}4 \end{matrix} \ast \begin{matrix} 0\\ -1\\ -0{,}4 \end{matrix} |}{| \begin{matrix} 0\\ -1\\ 0{,}4 \end{matrix}| \cdot | \begin{matrix} 0\\ -1\\ -0{,}4 \end{matrix}|} </math> | <math> cos(\beta)=\frac{ | \begin{matrix} 0\\ -1\\ 0{,}4 \end{matrix} \ast \begin{matrix} 0\\ -1\\ -0{,}4 \end{matrix} |}{| \begin{matrix} 0\\ -1\\ 0{,}4 \end{matrix}| \cdot | \begin{matrix} 0\\ -1\\ -0{,}4 \end{matrix}|} </math> | ||
<math> \Leftrightarrow cos(\beta)=\frac{\frac{21}{25}}{\sqrt{\frac{29}{25}} \cdot \sqrt{\frac{29}{25}}} \Leftrightarrow cos(\ | <math> \Leftrightarrow cos(\beta)=\frac{\frac{21}{25}}{\sqrt{\frac{29}{25}} \cdot \sqrt{\frac{29}{25}}} \Leftrightarrow cos(\beta)=\frac{\frac{21}{25}}{\frac{29}{25}} \Leftrightarrow cos(\beta)=\frac{21}{29}</math> | ||
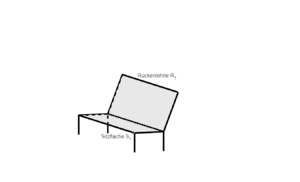
Umstellen der Formel ergibt: <math> \beta=cos^{-1} \left( \frac{21}{29} \right) \Leftrightarrow \beta \approx 43{,}6 ^\circ </math>. Der Winkel zwischen den beiden Rückenlehnen beträgt <math>43{,}6 ^\circ </math>.|2=Lösung anzeigen|3=Lösung verbergen}} | Umstellen der Formel ergibt: <math> \beta=cos^{-1} \left( \frac{21}{29} \right) \Leftrightarrow \beta \approx 43{,}6 ^\circ </math>. Der Winkel zwischen den beiden Rückenlehnen beträgt <math>43{,}6 ^\circ </math>.|2=Lösung anzeigen|3=Lösung verbergen}} | ||
| Arbeitsmethode}} | | Arbeitsmethode}} | ||
Version vom 6. Mai 2021, 21:01 Uhr
Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".
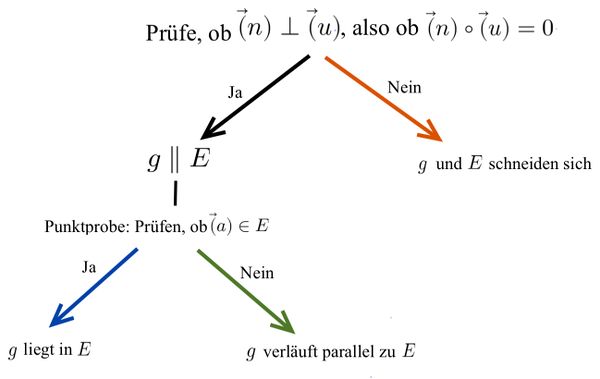
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
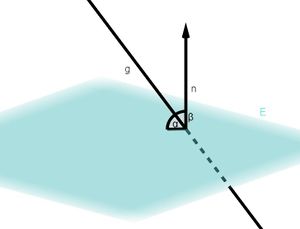
⭐Berechnung des Winkels zwischen Gerade und Ebene
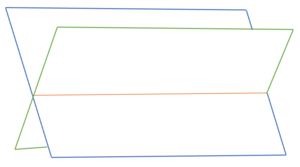
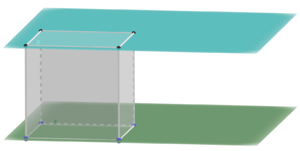
Lagebeziehung Ebene-Ebene
Basiswissen
⭐Berechnung des Winkels zwischen Ebene und Ebene