Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 141: | Zeile 141: | ||
{{Box | Beispiel: Berechnen des Winkels zwischen Gerade und Ebene | | {{Box | Beispiel: Berechnen des Winkels zwischen Gerade und Ebene | | ||
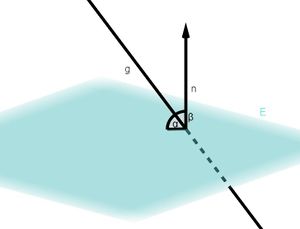
Gegeben sind die Gerade <math>g: \vec{x}=\left( \begin{matrix} -1\\ 3\\ 6 \end{matrix} \right) + r \cdot \left( \begin{matrix} 8\\ 2\\ 0 \end{matrix} \right) </math> und die Ebene <math>E: 2x_1 + x_2 + 4 x_3 = -27 </math>. Bestimme den Winkel unter dem sich die Gerade <math>g</math> und die Ebene <math>E</math> schneiden. | Gegeben sind die Gerade <math>g: \vec{x}=\left( \begin{matrix} -1\\ 3\\ 6 \end{matrix} \right) + r \cdot \left( \begin{matrix} 8\\ 2\\ 0 \end{matrix} \right) </math> und die Ebene <math>E: 2x_1 + x_2 + 4 x_3 = -27 </math>. Bestimme den Winkel unter dem sich die Gerade <math>g</math> und die Ebene <math>E</math> schneiden. | ||
| Zeile 226: | Zeile 227: | ||
{{Box | Merksatz: <Name> | Seien <math>E</math> und <math>F</math> zwei sich schneidende Ebenen mit den Normalenvektoren <math>n</math> und <math>m</math>. Der Schnittwinkel <math>\alpha</math> zwischen <math>E</math> und <math>F</math> kann mit folgender Formel berechnet werden: <math> cos(\alpha)=\frac{ \vec{n} \ast \vec{m}}{|\vec{n}| \cdot |\vec{m}|}</math>| Merksatz}} | {{Box | Merksatz: <Name> | Seien <math>E</math> und <math>F</math> zwei sich schneidende Ebenen mit den Normalenvektoren <math>n</math> und <math>m</math>. Der Schnittwinkel <math>\alpha</math> zwischen <math>E</math> und <math>F</math> kann mit folgender Formel berechnet werden: <math> cos(\alpha)=\frac{ \vec{n} \ast \vec{m}}{|\vec{n}| \cdot |\vec{m}|}</math>| Merksatz}} | ||
{{Box | Beispiel: Winkel berechnen zwischen zwei Ebenen | Gegeben sind zwei Ebenen <math>E</math> und <math>F</math> mit <math>E: \vec{x} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ 3 \\ -6 \end{pmatrix}+ s \cdot \begin{pmatrix} 1 \\ 1 \\ 0\end{pmatrix}, r,s \in \mathbb{R}</math> und <math>F: 7x_1+x_2-3x_3 </math>. Berechne den Schnittpunkt zwischen den Ebenen. | {{Box | Beispiel: Winkel berechnen zwischen zwei Ebenen | | ||
Gegeben sind zwei Ebenen <math>E</math> und <math>F</math> mit <math>E: \vec{x} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ 3 \\ -6 \end{pmatrix}+ s \cdot \begin{pmatrix} 1 \\ 1 \\ 0\end{pmatrix}, r,s \in \mathbb{R}</math> und <math>F: 7x_1+x_2-3x_3 </math>. Berechne den Schnittpunkt zwischen den Ebenen. | |||
'''1. Schritt:''' Bestimmte die Normalenvektoren von <math>E</math> und <math>F</math>. | '''1. Schritt:''' Bestimmte die Normalenvektoren von <math>E</math> und <math>F</math>. | ||
| Zeile 232: | Zeile 235: | ||
Der Normalenvektor von <math>E</math> kann mithilfe des ... bestimmt werden als <math>\vec{n} = \begin{pmatrix} 2 \\ -2 \\ -1 \end{pmatrix} </math> . Der Normalenvektor von <math>F</math> lautet <math>\vec{m} = \begin{pmatrix} 7 \\ 1 \\ -3 \end{pmatrix} </math>. | Der Normalenvektor von <math>E</math> kann mithilfe des ... bestimmt werden als <math>\vec{n} = \begin{pmatrix} 2 \\ -2 \\ -1 \end{pmatrix} </math> . Der Normalenvektor von <math>F</math> lautet <math>\vec{m} = \begin{pmatrix} 7 \\ 1 \\ -3 \end{pmatrix} </math>. | ||
'''2. Schritt''' Einsetzen der Normalenvektoren in die Formel. | '''2. Schritt:''' Einsetzen der Normalenvektoren in die Formel. | ||
<math>cos(\alpha) = \frac{ \left( \begin{pmatrix} 2 \\ -2 \\ -1 \end{pmatrix} \right) \ast \left( \begin{pmatrix} 7 \\ 1 \\ -3 \end{pmatrix \right)}}{\begin{pmatrix} 2 \\ -2 \\ -1 \end{pmatrix} \cdot \begin{pmatrix} 7 \\ 1 \\ -3 \end{pmatrix}} </math> | |||
<math> cos(\alpha)=\frac{ | <math>\Leftrightarrow cos(\alpha) = \frac{16}{3 \cdot \sqrt{59}}</math> | ||
'''3. Schritt:''' Auflösen der Gleichung. | |||
<math> \alpha = cos^{-1}(frac{16}{3 \cdot \sqrt {59}}) \Leftrightarrow \alpha \approx | |||
| Hervorhebung1}} | | Hervorhebung1}} | ||
{{Box | Aufgabe <Nummer>: Fehlerbeschreibung | Inhalt | Arbeitsmethode | Farbe={{Farbe|orange}} }} | {{Box | Aufgabe <Nummer>: Fehlerbeschreibung | Inhalt | Arbeitsmethode | Farbe={{Farbe|orange}} }} | ||
Version vom 6. Mai 2021, 20:47 Uhr
Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".
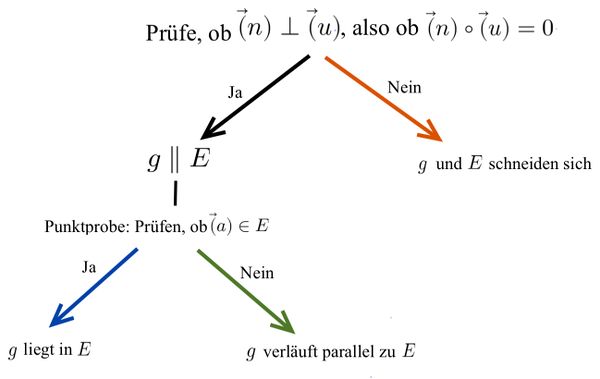
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
⭐Berechnung des Winkels zwischen Gerade und Ebene
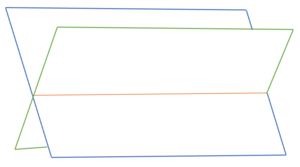
Lagebeziehung Ebene-Ebene
Basiswissen
⭐Berechnung des Winkels zwischen Ebene und Ebene