Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Abstände von Objekten im Raum: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 266: | Zeile 266: | ||
<math> P(p_1|p_2|p_3) </math> sei ein Punkt der Ebene <math>G</math>. | <math> P(p_1|p_2|p_3) </math> sei ein Punkt der Ebene <math>G</math>. | ||
Es gilt: <math> | Es gilt: <math>d(P;E)=\frac {|2p_1-3p_2+6p_3-13|}{\sqrt{2^2+(-3)^2+6^2}}=\frac{|2p_1-3p_2+6p_3-13|}{\sqrt{49}}=\frac {|2p_1-3p_2+6p_3-13|}{7}=\frac{|h-13|}{7}</math>. | ||
<math> | <math>d(P;E)=5 </math> nach Aufgabenstellung. Daher gilt: <math>\frac{h-13}{7}=5 </math> oder <math>\frac{h-13}{7}=-5 </math>. | ||
Stelle nun beide Gleichungen nach <math>h</math> um. | Stelle nun beide Gleichungen nach <math>h</math> um. | ||
| Zeile 326: | Zeile 326: | ||
# Stelle eine Hilfsebene <math>H</math> (in Koordinatenform) auf, die den Punkt <math>P</math> enthält und orthogonal zu zu <math>g</math> ist. Dafür kannst du als Stützvektor <math>\vec{p} </math> und als Normalenvektor den Richtungsvektor von <math>g</math> nehmen. | # Stelle eine Hilfsebene <math>H</math> (in Koordinatenform) auf, die den Punkt <math>P</math> enthält und orthogonal zu zu <math>g</math> ist. Dafür kannst du als Stützvektor <math>\vec{p} </math> und als Normalenvektor den Richtungsvektor von <math>g</math> nehmen. | ||
# Bestimme den Schnittpunkt <math>L</math> von <math>g</math> und <math>H</math> durch Einsetzen. | # Bestimme den Schnittpunkt <math>L</math> von <math>g</math> und <math>H</math> durch Einsetzen. | ||
# Berechne den Abstand <math>d(P | # Berechne den Abstand <math>d(P;g)=d(P;L)</math>. | ||
'''Verfahren Orthogonalität''' | '''Verfahren Orthogonalität''' | ||
# Bestimme einen allgmeinen Verbindungsvektor von <math>P</math> zu einem beliebigen Geradenpunkt <math>L</math> in Abhängigkeit vom Geradenparameter <math>r</math>. | # Bestimme einen allgmeinen Verbindungsvektor von <math>P</math> zu einem beliebigen Geradenpunkt <math>L</math> in Abhängigkeit vom Geradenparameter <math>r</math>. | ||
# Wähle <math>r</math> so, dass der Verbindungsvektor orthogonal zum Richtungsvektor der Geraden <math>g</math> ist. | # Wähle <math>r</math> so, dass der Verbindungsvektor orthogonal zum Richtungsvektor der Geraden <math>g</math> ist. | ||
# Berechne nun den Abstand <math>d(P | # Berechne nun den Abstand <math>d(P;g)=d(P;L)</math>. | ||
| 3=Merksatz}} | | 3=Merksatz}} | ||
| Zeile 370: | Zeile 370: | ||
<math> \Rightarrow L(-3|5|5) </math> | <math> \Rightarrow L(-3|5|5) </math> | ||
# Abstand <math>d(P | # Abstand <math>d(P;L)=d(P;L) </math> bestimmen: | ||
<math>d(P,L)=\sqrt{(-3-(-2))^2+(5-3)^2+(5+10)^2}=\sqrt{30}\approx 5,477</math> | <math>d(P,L)=\sqrt{(-3-(-2))^2+(5-3)^2+(5+10)^2}=\sqrt{30}\approx 5,477</math> | ||
| Zeile 396: | Zeile 396: | ||
Die Behauptung stimmt nicht. Den Flächeninhalt <math>F</math> eines Dreiecks kann man bekanntermaßen mit der Formel <math>F=\frac{1}{2}\cdot G \cdot h</math> berechnen, wobei <math>G</math> die Länge der Grundseite ist. | Die Behauptung stimmt nicht. Den Flächeninhalt <math>F</math> eines Dreiecks kann man bekanntermaßen mit der Formel <math>F=\frac{1}{2}\cdot G \cdot h</math> berechnen, wobei <math>G</math> die Länge der Grundseite ist. | ||
In dieser Aufgabe bleibt der Abstand <math> | In dieser Aufgabe bleibt der Abstand <math>d(A;g)</math> immer gleich, da sich <math>A</math> auf einer zu <math>g</math> parallelen Geraden "bewegt". Also ist die Höhe <math>h</math> all dieser Dreiecke gleich. Deshalb ändert sich auch der Flächeninhalt <math>F=\frac{1}{2}\cdot G \cdot h</math> nicht. | ||
|2=Lösung zu a) anzeigen|3=Lösung zu a) verbergen}} | |2=Lösung zu a) anzeigen|3=Lösung zu a) verbergen}} | ||
| Zeile 406: | Zeile 406: | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Wir bestimmen zunächst die Länge <math>G</math> der Grundseite: | Wir bestimmen zunächst die Länge <math>G</math> der Grundseite: | ||
Es <math> | Es <math>d(B;C)=\sqrt((2-0,5)^2+(8-3,5)^2+(1-7)^2)=\sqrt(58,5)</math>. | ||
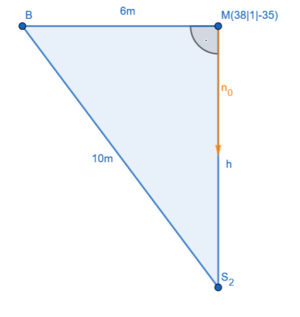
Nun bestimmen wir die Höhe <math>h</math>, also den Abstand der parallelen Geraden <math>g</math> und <math>j</math> mithilfe des Verbindungsvektors von <math>B</math> zur Geraden <math>j</math>.(Da die Geraden parallel sind, ist es natürlich egal, welche der Geraden und welchen Punkt auf der anderen Geraden man nimmt. Ihr könntet ebenso mit dem anderen Verfahren, also mit einer Hilfsebene arbeiten): | Nun bestimmen wir die Höhe <math>h</math>, also den Abstand der parallelen Geraden <math>g</math> und <math>j</math> mithilfe des Verbindungsvektors von <math>B</math> zur Geraden <math>j</math>.(Da die Geraden parallel sind, ist es natürlich egal, welche der Geraden und welchen Punkt auf der anderen Geraden man nimmt. Ihr könntet ebenso mit dem anderen Verfahren, also mit einer Hilfsebene arbeiten): | ||
Der Punkt <math>L_s=(1+t|1+3t|2-4t)</math> ist ein allgemeiner Punkt auf <math>j</math>. Ein allgemeiner Verbindungsvektor zwischen <math>B</math> und <math>j</math> ist also gegeben durch <math>\vec{BL_s}=\begin{pmatrix} (1+t)-2 \\ (1+3t)-8 \\ (2-4t)-1 \end{pmatrix}=\begin{pmatrix} -1+t \\ -7+3t \\ 1-4t \end{pmatrix}</math>. | Der Punkt <math>L_s=(1+t|1+3t|2-4t)</math> ist ein allgemeiner Punkt auf <math>j</math>. Ein allgemeiner Verbindungsvektor zwischen <math>B</math> und <math>j</math> ist also gegeben durch <math>\vec{BL_s}=\begin{pmatrix} (1+t)-2 \\ (1+3t)-8 \\ (2-4t)-1 \end{pmatrix}=\begin{pmatrix} -1+t \\ -7+3t \\ 1-4t \end{pmatrix}</math>. | ||
Damit <math>\vec{BL_s}</math> orthogonal zum Richtungsvektor von <math>j</math> ist, muss gelten: | Damit <math>\vec{BL_s}</math> orthogonal zum Richtungsvektor von <math>j</math> ist, muss gelten: | ||
<math>\begin{pmatrix} -1+t \\ -7+3t \\ 1-4t \end{pmatrix}\cdot \begin{pmatrix} 1 \\ 3 \\ -4 \end{pmatrix}=0 </math> bzw. <math>(t-1)\cdot 1+(-7+3t)\cdot 3 + (1-4t) \cdot (-4)</math>, also <math>t=1</math>. Für <math>L=(2|4|-2)</math> ist der Verbindungsvektor also am kürzesten. Somit ist <math>h= | <math>\begin{pmatrix} -1+t \\ -7+3t \\ 1-4t \end{pmatrix}\cdot \begin{pmatrix} 1 \\ 3 \\ -4 \end{pmatrix}=0 </math> bzw. <math>(t-1)\cdot 1+(-7+3t)\cdot 3 + (1-4t) \cdot (-4)</math>, also <math>t=1</math>. Für <math>L=(2|4|-2)</math> ist der Verbindungsvektor also am kürzesten. Somit ist <math>h=d(B;j)=d(B;L)=\sqrt((2-2)^2+(4-8)^2+(-2-1)^2)=\sqrt(25)=5</math>. | ||
Der Flächeninhalt des Dreiecks beträgt also <math>F=\frac{1}{2}\cdot G \cdot h=\frac{1}{2}\cdot \sqrt(58,5) \cdot 5\approx 19,12</math> Flächeneinheiten. | Der Flächeninhalt des Dreiecks beträgt also <math>F=\frac{1}{2}\cdot G \cdot h=\frac{1}{2}\cdot \sqrt(58,5) \cdot 5\approx 19,12</math> Flächeneinheiten. | ||
| Zeile 435: | Zeile 436: | ||
Der Abstand zweier windschiefer Geraden <math>g</math> und <math>h</math> ist die kleinste Entfernung zwischen den Punkten von <math>g</math> und den Punkten von <math>h</math>. Diese kürzeste Verbindungsstrecke <math>\overline{GH}</math> zwischen den beiden Geraden ist sowohl orthogonal zu <math>g</math> als auch orthogonal zu <math>h</math> und heißt gemeinsames Lot der windschiefen Geraden <math>g</math> und <math>h</math>. | Der Abstand zweier windschiefer Geraden <math>g</math> und <math>h</math> ist die kleinste Entfernung zwischen den Punkten von <math>g</math> und den Punkten von <math>h</math>. Diese kürzeste Verbindungsstrecke <math>\overline{GH}</math> zwischen den beiden Geraden ist sowohl orthogonal zu <math>g</math> als auch orthogonal zu <math>h</math> und heißt gemeinsames Lot der windschiefen Geraden <math>g</math> und <math>h</math>. | ||
Für die Bestimmung des Abstandes <math>d(g | Für die Bestimmung des Abstandes <math>d(g;h)</math> berechnet man also die Länge des gemeinsamen Lotes der Geraden. Dafür gibt es wieder verschiedene Möglichkeiten. Hier werden zwei Verfahren noch einmal zusammengefasst: | ||
Seien <math>g: \vec{x}=\vec{p}+s\cdot \vec{u}</math> und <math>h: \vec{x}=\vec{q}+t\cdot \vec{v}</math> die windschiefen Geraden. | Seien <math>g: \vec{x}=\vec{p}+s\cdot \vec{u}</math> und <math>h: \vec{x}=\vec{q}+t\cdot \vec{v}</math> die windschiefen Geraden. | ||
| Zeile 443: | Zeile 444: | ||
# Stelle den Verbindungsvektor <math>\vec{G_s H_t}</math> in Abhängigkeit von den Geradenparametern auf. | # Stelle den Verbindungsvektor <math>\vec{G_s H_t}</math> in Abhängigkeit von den Geradenparametern auf. | ||
# Bestimme nun die Parameter <math>s</math> und <math>t</math> so, dass der Verbindungsvektor <math>\vec{G_s H_t}</math> orthogonal zu den Richtungsvektoren von <math>g</math> und <math>h</math> ist. Du löst also das lineare Gleichungssystem mit den beiden Gleichungen <math>\vec{G_s H_t}\cdot \vec{u} =0</math> und <math>\vec{G_s H_t}\cdot \vec{v} =0</math>. | # Bestimme nun die Parameter <math>s</math> und <math>t</math> so, dass der Verbindungsvektor <math>\vec{G_s H_t}</math> orthogonal zu den Richtungsvektoren von <math>g</math> und <math>h</math> ist. Du löst also das lineare Gleichungssystem mit den beiden Gleichungen <math>\vec{G_s H_t}\cdot \vec{u} =0</math> und <math>\vec{G_s H_t}\cdot \vec{v} =0</math>. | ||
# Mit diesen Parametern erhältst du die Lotfußpunkte <math>G</math> und <math>H</math> und kannst den Abstand <math>d(g | # Mit diesen Parametern erhältst du die Lotfußpunkte <math>G</math> und <math>H</math> und kannst den Abstand <math>d(g;h)=d(G;H)</math> bestimmen. | ||
'''Verfahren Hilfsebene''' | '''Verfahren Hilfsebene''' | ||
| Zeile 451: | Zeile 452: | ||
# Bestimme aus den Gleichungen <math>\vec{u}\cdot\vec{n}=0</math> und <math>\vec{v}\cdot\vec{n}=0</math> einen Normalenvektor. | # Bestimme aus den Gleichungen <math>\vec{u}\cdot\vec{n}=0</math> und <math>\vec{v}\cdot\vec{n}=0</math> einen Normalenvektor. | ||
# Stelle die Normalengleichung <math>(\vec{x}-\vec{p})\cdot\vec{n}=0</math> der Ebene <math>E</math> auf. | # Stelle die Normalengleichung <math>(\vec{x}-\vec{p})\cdot\vec{n}=0</math> der Ebene <math>E</math> auf. | ||
# Bestimme mit der Hesse´schen Normalenform oder dem Lotfußpunktverfahren (siehe Abschnitt Abstand Punkt Ebene) den Abstand <math>d(E | # Bestimme mit der Hesse´schen Normalenform oder dem Lotfußpunktverfahren (siehe Abschnitt Abstand Punkt Ebene) den Abstand <math>d(E;H)=d(g;h)</math>. | ||
| Zeile 516: | Zeile 517: | ||
| 3=Arbeitsmethode| Farbe={{Farbe|blau}}}} | | 3=Arbeitsmethode| Farbe={{Farbe|blau}}}} | ||
Version vom 6. Mai 2021, 20:33 Uhr
Einstieg
Abstand eines Punktes von einer Ebene
Das Lotfußpunktverfahren
Die Hesse´sche Normalenform
Um den Abstand zwischen einem Punkt und einer Ebene zu bestimmen, gibt es neben dem Lotverfahren auch die Möglichkeit, dies mit der Hesse´schen Normalenform zu berechnen. In diesem Abschnitt lernst du, wie du die Normalenform aufstellst und sie zur Abstandsberechnung anwendest.
Falls du noch nicht genug hast, kannst du auch versuchen, die Aufgaben vom Lotfußpunktverfahren mit der Hesse´schen Normalenform zu lösen.
Abstand eines Punktes von einer Geraden
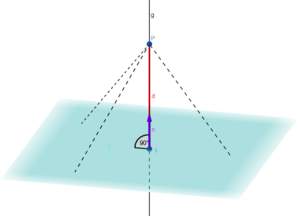
Abstand zweier windschiefer Geraden
Verschiebe die Punkte und so, dass die kürzeste Verbindungsstrecke zwischen den windschiefen Geraden und ist. Du kannst die Grafik mit deiner Maus drehen, um die Geraden aus anderen Perspektiven zu betrachten.