Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung |
||
| Zeile 69: | Zeile 69: | ||
|Arbeitsmethode}} | |Arbeitsmethode}} | ||
{{Box | Aufgabe <Nummer>: Schattenpunkt einer Pyramide | | {{Box | Aufgabe <Nummer>: Schattenpunkt einer Pyramide | | ||
Da es Frau Meier im Sommer auf ihrer Terrasse gerne schattig haben möchte, spannt sie ein dreieckiges Segeltuch auf. Die Eckpunkte des Segeltuchs sind <math> A = \left( \begin{matrix} 9\\ -5\\ 7 \end{matrix} \right), B= \left( \begin{matrix} 6\\ -5\\ 7 \end{matrix} \right)</math> und <math> C = \left( \begin{matrix} 7\\ -10\\ 11 \end{matrix} \right) </math>. Die Terrasse wird modelliert durch die <math>x_1- x_2</math>-Ebene. Die Sonne scheint aus Richtung <math> S = \left( \begin{matrix} -2\\ -2\\ -10 \end{matrix} \right) </math>. In welchem Bereich hat Frau Meier nun Schatten? | |||
{{Lösung versteckt|1= Die <math> x_1-x_2 </math>-Ebene wird z.B. durch die Gleichung <math> E: \vec{x}=\left( \begin{matrix} 0\\ 0\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} 1\\ 0\\ 0 \end{matrix} \right) + t \cdot \left( \begin{matrix} 0\\ 1\\ 0 \end{matrix} \right) </math> beschrieben.|2=Tipp 1 anzeigen|3=Tipp 1 verbergen}} | |||
{{Lösung versteckt|1= Bestimme die Geraden der Lichtstrahlen durch die Eckpunkte des Sonnensegels und berechne, wo sie auf die Terrasse treffen. Vielleicht hilft dir eine Skizze.|2=Tipp 2 anzeigen|3=Tipp 2 verbergen}} | |||
| Arbeitsmethode}} | |||
{{Box|⭐Merke: Lagebeziehung von Gerade und Ebene untersuchen mit Ebene in Koordinatenform. | | {{Box|⭐Merke: Lagebeziehung von Gerade und Ebene untersuchen mit Ebene in Koordinatenform. | | ||
Version vom 6. Mai 2021, 15:44 Uhr
Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".
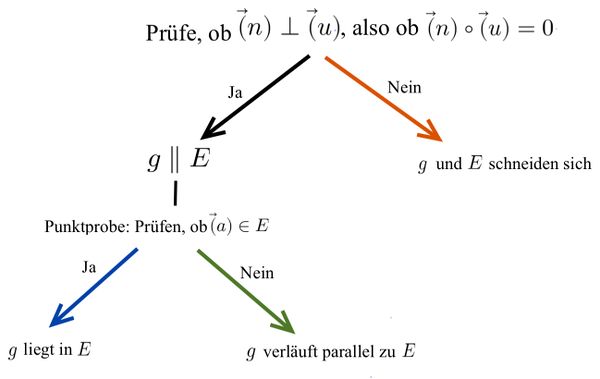
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
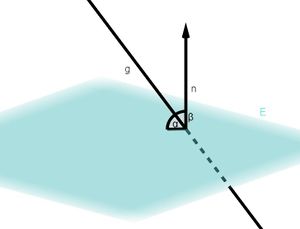
⭐Berechnung des Winkels zwischen Gerade und Ebene
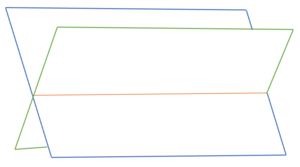
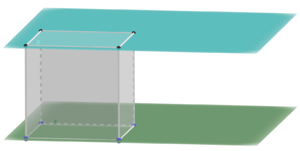
Lagebeziehung Ebene-Ebene
Basiswissen
⭐Berechnung des Winkels zwischen Ebene und Ebene