Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 35: | Zeile 35: | ||
1. Schritt: Setze die Geraden- und Ebenengleichung gleich. | '''1. Schritt:''' Setze die Geraden- und Ebenengleichung gleich. | ||
<math>\left( \begin{matrix} 1\\ 0\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} -1\\ 1\\ 0 \end{matrix} \right) + t \cdot \left( \begin{matrix} -1\\ 0\\ 1 \end{matrix} \right) = \left( \begin{matrix} 2\\ 2\\ 2 \end{matrix} \right) + r \cdot \left( \begin{matrix} -1\\ -4\\ 0 \end{matrix} \right) </math> | |||
2. Schritt: Stelle das zugehörige lineare Gleichungssystem auf. | '''2. Schritt:''' Stelle das zugehörige lineare Gleichungssystem auf. | ||
<math> \begin{vmatrix} 1-s-t=2-r \\ s=2-4r \\ t=2 \end{vmatrix} </math> | |||
3. Schritt: Löse das Gleichungssystem mit dem Gaußverfahren oder dem Taschenrechner. | '''3. Schritt:''' Löse das Gleichungssystem mit dem Gaußverfahren oder dem Taschenrechner. | ||
<math>s=-1, t=2, r=1 </math> | |||
'''4. Schritt:''' Interpretiere die Lösung des Gleichungssystems anhand der Anzahl der Lösungen. | |||
Da das Gleichungssystem nur eine Lösung hat, besitzen die Ebene <math>E</math> und die Gerade <math>g</math> nur einen gemeinsamen Punkt. Also schneidet die Gerade die Ebene. | |||
'''5. Schritt:''' Da sich die Ebene <math>E</math> und die Gerade <math>g</math> schneiden, kannst du den Schnittpunkt der beiden berechnen. Setze dafür den Parameter <math>r</math> in die Geradengleichung ein. | |||
<math>g: \left( \begin{matrix} 2\\ 2\\ 2 \end{matrix} \right) + 1 \cdot \left( \begin{matrix} -1\\ -4\\ 0 \end{matrix} \right) = \left( \begin{matrix} 1\\ -2\\ 2 \end{matrix} \right) </math> | |||
| Hervorhebung1}} | | Hervorhebung1}} | ||
Version vom 5. Mai 2021, 15:37 Uhr
dHier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".
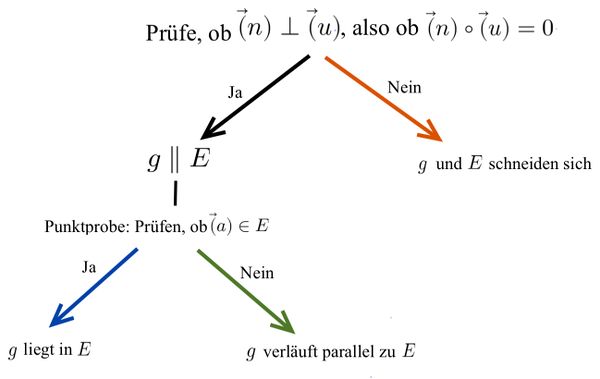
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
⭐Berechnung des Winkels zwischen Gerade und Ebene
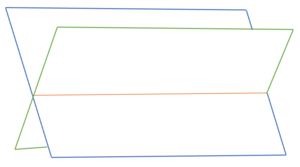
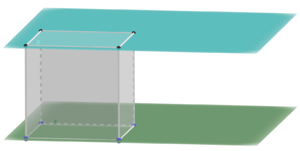
Lagebeziehung Ebene-Ebene
Basiswissen
⭐Berechnung des Winkels zwischen Ebene und Ebene