Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Abstände von Objekten im Raum

Info

In diesem Lernpfadkapitel kannst du wiederholen, wie du Abstände von Objekten im Raum bestimmst. Du übst den Abstand von einer Ebene zu einem Punkt, von einer Geraden zu einem Punkt und von zwei windschiefen Geraden zu bestimmen. Am Ende findest du noch einige gemischte Aufgaben. Dieses Thema ist nur für den LK gedacht, daher sind alle Aufgaben auch automatisch LK-Aufgaben und nicht noch jeweils mit einem ⭐ gekennzeichnet.

Bei den Aufgaben unterscheiden wir folgende Typen:

• In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit.
• Und Aufgaben mit grünem Streifen sind Knobelaufgaben.

Viel Erfolg!

Motivation?

• ganz am Anfang, zur Motivation: 3 Situationen, zuordnen lassen, welche Punkt-Ebene, Punkt-Gerade usw. ist (mit Learning App), mit Bild

Abstand eines Punktes von einer Ebene

Das Lotfußpunktverfahren

Aufgabe 1: Überblick: Abstand Punkt Ebene

Abstand Punkt Ebene

Bei dieser Aufgabe kannst du einen Überblick über die Bestimmung des Abstandes zwischen einem Punkt und einer Ebene mit dem Lotfußpunktverfahren bekommen. Es geht auch um wichtige Begriffe in diesem Zusammenhang.

Fülle die Lücken mit den richtigen Wörtern. Sie werden dir angezeigt, sobald du auf eine Lücke klickst. Wenn du fertig bist, klicke auf den Haken unten rechts.

Die Abbildung kann dir helfen.

Merke: Abstand eines Punktes P zu einer Ebene E - Lotfußpunktverfahren

Das Vorgehen aus Aufgabe 1 hier nochmal detalliert erklärt:

1. Die Gleichung für die zu $E$ orthogonale Gerade $g$ (also die Lotgerade) durch $P$ aufstellen. Dabei kann man als Stützvektor $\vec{p}$ und als Richtungsvektor den Normalenvektor $\vec{n}$ von $E$ nutzen: $g:\vec{x}=\vec{p}+\vec{t}\cdot\vec{n}$.
2. Den Schnittpunkt $L$ von der Lotgeraden $g$ und der Ebene $E$ bestimmen. $L$ ist der Lotfußpunkt.
3. Den Abstand zwischen den Punkten $P$ und $L$ bestimmen, indem man den Betrag des Vektors $\vec{PL}$ berechnet.

Aufgabe 2: Abstände von Punkt-Ebene zuordnen

Berechne die Abstände der verschiedenen Ebenen $E, F, G$ zum Punkt $P(3|4|-2)$. Ordne dann den Ebenen dem jeweiligen Abstand $d$ zu.

Ziehe dazu den passenden Abstand auf die jeweilige Ebene. Möchtest du eine Karte vergrößern, klicke auf die drauf. Klicke am Ende auf den Haken unten rechts, um dich selbst zu überprüfen.

Viel Spaß!

Du kannst auch immer die Hesse´sche Normalenform zur Berechnung benutzten. Im Folgenden wurden die Abstände mit dem Lotfußpunktverfahren berechnet.

Abstand von $E:2x_1+6x_2-4x_3=-32$ und $P(3|4|-2)$:

Die Gleichung für die zu $E:2x_1+6x_2-4x_3=1$ orthogonale Gerade $g$ (also die Lotgerade) durch $P(3|4|-2)$ aufstellen:

$l:\vec{x}=\vec{p}+t\cdot\vec{n}=\begin{pmatrix} 3 \\ 4 \\ -2 \end{pmatrix}+t\cdot\begin{pmatrix} 2 \\ 6 \\ -4 \end{pmatrix}$.

Den Lotfußpunkt $A$ bestimmen:

$E:2(3+2t)+6(4+6t)-4(-2-4t)=32 \Rightarrow t=-1,25$

$t$ in $l$ einsetzten:

$l:\vec{x}=\begin{pmatrix} 3 \\ 4 \\ -2 \end{pmatrix}-1,25\cdot\begin{pmatrix} 2 \\ 6 \\ -4 \end{pmatrix}=\begin{pmatrix} 0,5 \\ -3,5 \\ 3 \end{pmatrix}$

Der Lotfußpunkt $A$ ist $A(0,5|-3,5|3)$.

Den Abstand zwischen den Punkten $P$ und $A$ bestimmen:

$d(P,A)=|\vec{P,A}|=\sqrt((0,5-3)^2+(-3,5-4)^2+(3-(-2))^2)\approx 9,354$

$\Rightarrow d\approx 9,354$

Abstand von $F:\begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix}\cdot(\vec{x}-\begin{pmatrix} 6 \\ -2 \\ 3 \end{pmatrix}) )=0$ und $P(3|4|-2)$:

$F$ in Koordinatenform umschreiben:

$F:\begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix}\cdot(\vec{x}-\begin{pmatrix} 6 \\ -2 \\ 3 \end{pmatrix})=0 \Leftrightarrow F: x_1+x_2+2x_3=10$

Wenn du hierbei noch Probleme hast, dann schau dir doch nochmal Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum an.

Zu $F$ senkrechte Gerade $m$ durch $P$ aufstellen: $m:\vec{x}=\begin{pmatrix} 3 \\ 4 \\ -2 \end{pmatrix}+s\cdot\begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix}$

Koordinaten der Geradengleichung $m$ in $F$ einsetzten:

$F:(3+s)+(4+s)+2(-2+2s)=10 \Leftrightarrow s=\frac{7}{6}$

$m:\vec{x}=\begin{pmatrix} 3 \\ 4 \\ -2 \end{pmatrix}+\frac{7}{6}\cdot\begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix}=\begin{pmatrix} \frac{25}{6} \\ \frac{31}{6} \\ \frac{1}{3} \end{pmatrix}$

Der Lotfußpunkt $B$ ist $B(\frac{25}{6}|\frac{31}{6}|\frac{1}{3})$.

Den Abstand zwischen den Punkten $P$ und $B$ bestimmen:

$d(P,B)=|\vec{P,B}|=\sqrt((\frac{25}{6}-3)^2+(\frac{31}{6}-4)^2+(\frac{1}{3}-(-2))^2)\approx 2,858$

$\Rightarrow d\approx 2,858$

Abstand von der $x_1x_2-Ebene$ zum Punkt $P(3|4|-2)$:

Sollst du den Abstand eines Punktes zu einer Koordinatenebene bestimmen, so kannst du diesen einfach ablesen und musst ihn nicht berechnen. Der Abstand hier beträgt $2$, da $|-2|$ die $x_3$ Koordinate von $P$ ist und damit den Abstand zur $x_1x_2-Ebene$ anzeigt.

Beachte: ein Abstand ist immer positiv und da $|-2|=2$ ist der Abstand $2$.

$\Rightarrow d=2$

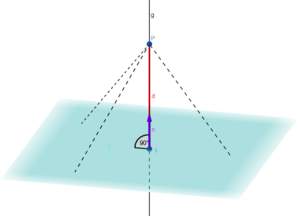
Aufgabe 3: Glaspyramide

a) Im Innenhof des Louvre-Museums in Paris befindet sich eine große Glaspyramide. Die quadratische Grundfläche liegt in einer Ebene, die durch die Ebenengleichung $E: 2x_1+x_2+2x_3=7$ beschrieben werden kann. Die Spitze liegt im Punkt $S(4,5|9|3,5)$. Eine Längeneinheit $LE$ im Koordinatensystem entpricht $4m$.

Welche Höhe hat die Pyramide in $m$?

Text zum Verstecken

Die Höhe der Pyramide kann man bestimmen, indem man den Abstand zwischen der Spitze $S$ und der Ebene $E$ bestimmt.

Zuerst wird die Geradengleichung der Lotgeraden $g$ zu $E$ durch $P$ aufgestellt. Wir nehmen den Ortsvektor von $S$ als Stützvektor und den Normalenvektor von $E$ als Richtungsvektor, also: $g: \vec{x}= \begin{pmatrix} 4,5 \\ 9 \\ 3,5 \end{pmatrix}+ t \cdot \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix}$.

Wir bestimmen den Schnittpunkt von $g$ mit $E$. Einsetzen von einem allgemeinen Punkt von $g$ in $E$ ergibt $(4,5+2t)+(9+t)+2(3,5+2t)=7$, also $t=-2$. Durch Einsetzen in die Geradengleichung $\begin{pmatrix} 4,5 \\ 9 \\ 3,5 \end{pmatrix}- 2 \cdot \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix} = \begin{pmatrix} 0,5 \\ 7 \\ -0,5 \end{pmatrix}$ erhalten wir den Lotfußpunkt $L(0,5|7|-0,5)$. Dies ist gleichtzeitig der Mittelpunkt der Grundfläche der Glaspyramide.

Der Abstand zwischen S und L beträgt $6LE$ wegen $|\vec{SL}|=\sqrt((4,5-0,5)^2+(9-7)^2+(3,5-(-0,5))^2)=6$. Die Pyramide hat also eine Höhe von $24m$.

Die Pyramide hat eine Höhe von $24m$.

Spitze der invertierten Glaspyramide

b) An einer anderen Stelle im Innenhof des Louvre befindet sich eine invertierte Glaspyramide. Das bedeutet, ihre quadratische Grundfläche liegt in der gleichen Ebene wie die Grundfläche der großen Glaspyramide, ihre Spitze ist aber unterhalb des Innenhofs. Man kann sie in einem Raum unterhalb des Innenhofs besichtigen. Die Länge der Kante von der Spitze bis zu einer Ecken der Grundfläche beträgt jeweils $10m$. Die Grundfläche hat $12m$ lange Diagonalen, die sich im Punkt $(38 | 1 | -35)$ schneiden. In welchem Punkt $S_2$ liegt die Spitze der umgedrehten Pyramide?

Zeichne eine Skizze, in der du alle bekannten Längenangaben und Punkte einträgst. Was musst du wissen, um die Position der Spitze herauszufinden?

Wenn du die Höhe der Pyramide kennst, weißt du, welche Abstand die Spitze von der Grundfläche hat. Du kennst auch schon den Mittelpunkt der Pyramiden und kannst entlang des Normalenvektors von $E$ zur Spitze gelangen.

Du kannst die Höhe der Pyramide mithilfe des Satzes von Pythagoras und der Längenangaben berechnen.

Die Höhe der Pyramide kann man mit dem Satz des Pythagoras und den Längenangaben für die Diagonale der Grundfläche und die Kanten berechnen:

Es ist $\sqrt{10^2-6^2}=\sqrt(64)=8$, also beträgt die Höhe der invertierten Pyramide $8m$, was $2LE$ im Koordinatensystem entspricht.

Die Spitze der umgedrehten Pyramide liegt also in einem Punkt, der einen Abstand von $2LE$ zur Pyramidengrundfläche hat. Es gibt genau zwei solche Punkte, die Spitze einer "normalen" Pyramide und die Spitze der invertierten Pyramide.

Damit man die Spitze der invertierten Pyramide erhält, geht man vom Mittelpunkt $M (38 | 1 | -35)$ der Grundfläche aus $2LE$ entlang der Geraden, die orthogonal zu $E$ ist, und zwar in die andere Richtung als in Aufgabenteil a). Das heißt, man geht $2LE$ in die entgegengesetzte Richung des Normalenvekotrs von $E$.

Es ist $|vec{n}|=|\begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix}|=\sqrt{2^2+1^2+2^2}=3, also ist vec{n_0}=\frac{1}{3}\begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix}$.

Nun können wir bestimmen, in welchem Punkt $S_2$ die Spitze liegt:

Es ist $\begin{pmatrix} 38 \\ 1 \\ -35 \end{pmatrix}\cdot \frac{1}{3}\begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix}=\begin{pmatrix} 36 \frac{2}{3} \\ \frac{1}{3} \\ -36 \frac{1}{3} \end{pmatrix}$, also erhält man $S_2=(36 \frac{2}{3}|\frac{1}{3}|-36 \frac{1}{3})$

Die Spitze der invertierten Pyramide liegt im Punkt $S_2=(36 \frac{2}{3}|\frac{1}{3}|-36 \frac{1}{3})$.

Die Hesse´sche Normalenform

Um den Abstand zwischen einem Punkt und einer Ebene zu bestimmen, gibt es neben dem Lotverfahren auch die Möglichkeit, dies mit der Hesse´schen Normalenform zu berechnen. In diesem Kapitel lernst du, wie du die Normalenform aufstellst und sie zur Abstandsberechnung anwendest.

Merke: Die Hesse´sche Normalenform

Den Abstand von einem Punkt $P$ zu einer Ebene $E$ kann mit einer Formel berechnet werden, der sogenannten Hesse´schen Normalenform (kurz:HNF).

So bestimmst du mit der HNF den Abstand:

Gegeben ist eine Ebene $E$ durch die Koordinatengleichung $a\cdot x_1+b\cdot x_2+c\cdot x_3=d$ bzw. durch die Normalenform $\vec{n}\cdot\vec{OX}$ mit $\vec{n}= \begin{pmatrix} a \\ b \\ c \end{pmatrix}$ und ein Punkt $P(p_1|p_2|p_3)$.

Stelle nun die HNF der Ebene auf:

Lies dazu aus der Koordinatengleichung der Ebene den Normalenvektor $\vec{n}= \begin{pmatrix} a \\ b \\ c \end{pmatrix}$ ab.

Bestimme dann die Länge des Normalenvektors $\vec{n}$: $|\vec{n}|=\sqrt{a^2+b^2+c^2}$

Die HNF lautet nun: $\frac {|a\cdot x_1+b\cdot x_2+c\cdot x_3-d|}{|\vec{n}|}$.

Als letztes setzte die Koordinaten des Punktes $P(p_1|p_2|p_3)$ in die HNF ein und berechne den Abstand:

$\frac {|a\cdot p_1+b\cdot p_2+c\cdot p_3-d|}{|\vec{n}|}$

Aufgabe 4:

Über dem Schuldach schwebt eine Drohne an der Stelle $A(3|4|-1)$ und ein Falke schwebt auf der Stelle $B(1|7|4)$. Finde heraus, wer den geringeren Abstand zum Schuldach hat. Das Schuldach lässt sich durch folgende Gleichung beschreiben: $E: 8x_1-4x_2-x_3=5$.

Der Normalenvektor der Ebene ist: $\vec{n}= \begin{pmatrix} 8 \\ -4 \\ -1 \end{pmatrix}$

Länge des Normalenvektors $\vec{n}$ bestimmen: $|\vec{n}|=\sqrt{8^2-4^2+(-1)^2}=\sqrt{64+16+1}=\sqrt{81}=9$

Die HNF lautet nun: $\frac {|8\cdot x_1-4\cdot x_2-1\cdot x_3-5|}{9}$.

Nun werden die Koordinaten von $A$ eingesetzt: $\frac {|8\cdot3-4\cdot4-1\cdot(-1)-5|}{9}=\frac {|24-26+1-5|}{9}=\frac {|-6|}{9}=\frac {6}{9}=\frac {2}{3}$

Die Koordinaten von $B$ können in die selbe HNF eingesetzt werden: $\frac {|8\cdot(-1)-4\cdot7-1\cdot4-5|}{9}=\frac {|-8-28-4-5|}{9}=\frac {|-45|}{9}=5$.

Damit hat die Drohne einen Abstand von $\frac{2}{3}$ zum Schuldach und der Falke einen Abstand von $5$. Die Drohne ist also näher zum Dach als der Vogel.

Der Abstand der Drohne zum Dach beträgt $\frac{2}{3}$ und der Abstand des Falken zum Dach beträgt $5$. Damit ist der Abstand der Drohne geriner.

Aufgabe 2: Abstand paralleler Ebenen

Gegeben ist die Ebene $E: 2x_1-3x_2+6x_3=13$. Bestimme zur Ebene $E$ zwei parallele Ebenen, die von $E$ den Abstand $5$ haben.

Überlege dir, welchen Normalenvektor die Ebenen haben müssen, damit sie parallel zu $E$ sind

Die gesuchten Ebenen haben den gleichen Normalenvektor wie $E$.

Ansatz: $G:2x_1-3x_2+6x_3=h$

$P(p_1|p_2|p_3)$ sei ein Punkt der Ebene $G$.

Es gilt: $Abst(P;E)=\frac {|2p_1-3p_2+6p_3-13|}{\sqrt{2^2-3^2+6^2}}=\frac{|2p_1-3p_2+6p_3-13|}{\sqrt{49}}=\frac {|2p_1-3p_2+6p_3-13|}{7}=\frac{|h-13|}{7}$.

$Abst(P;E)=5$ nach Aufgabenstellung. Daher gilt: $\frac{h-13}{7}=5$ oder $\frac{h-13}{7}=-5$.

Stelle nun beide Gleichungen nach $h$ um. Es folgt: $h_1=48$ und $h_2=-22$.

Dies wird nun in die Ebenengleichung von $G$ eingesetzt:

$G_1:2x_1-3x_2+6x_3=48$ $G_2:2x_1-3x_2+6x_3=-22$

$G_1$ und $G_2$ haben nun beide den Abstand $5$ zur Ebene $E$.

$G_1:2x_1-3x_2+6x_3=48$ und $G_2:2x_1-3x_2+6x_3=-22$

haben beide den Abstand $5$ zu $E$.

Falls du noch nicht genug hast, kannst du auch versuchen, die Aufgaben vom Lotfußpunktverfahren mit der Hesse´schen Normalenform zu lösen.

Abstand eines Punktes von einer Geraden

Aufgabe 5 Grafische Darstellung: Abstand eines Punktes von einer Geraden

Bewege den Punkt $Q$ auf der Geraden $g$, um dir den jeweiligen Abstand zwischen den Punkten $P$ und $Q$ anzeigen zu lassen. Rechts neben der Geraden siehst du, wie groß der Abstand jeweils ist.

Wann ist der Abstand vom Punkt $P$ zur Geraden $g$ am kleinsten?

Wie groß ist der Winkel zwischen $g$ und der Geraden durch $P$ und $Q$? Wie nennt man $Q$ dann?

Versuche es zuerst ohne die Hilfslinie. Überprüfe dich dann selbst.

Dies ist der Link zur GeoGebra App, falls die Anzeige bei dir nicht funktioniert:https://www.geogebra.org/material/show/id/cFTUcwnd#

Der Abstand $Abst(P,Q)=d(P,g)$ ist am kleinsten, wenn $vec{PQ}$ orthogonal zu $g$ ist. Dies kannst du sehen, wenn du dir die Hilfslinie anzeigen lässt.

Dann nennt man den Punkt $Q$ den Lotfußpunkt von $P$ auf $g$.

Merke: Der Abstand eines Punktes zu einer Geraden

Der Abstand eines Punktes $P$ zu einer Geraden $g$ ist der Abstand von $P$ und $L$, wobei $L$ der Lotfußpunkt von $P$ auf $g$ ist.

Für die Bestimmung des Abstandes $d(P,g)=d(P,G)$ gibt es zwei verschiedene Verfahren:

1. Verfahren (Hilfsebene): Stelle eine Hilfsebene $H$ (in Koordinatenform) auf, die den Punkt $P$ enthält und orthogonal zu zu $g$ ist. Dafür kannst du als Stützvektor $\vec{p}$ und als Normalenvektor den Richtungsvektor von $g$ nehmen. Bestimme den Schnittpunkt $L$ von $g$ und $H$ durch Einsetzen. Zuletzt berechne den Abstand $d(P,g)=d(P,L)$.

2. Verfahren (Orthogonalität): Bestimme einen allgmeinen Verbindungsvektor von $P$ zu einem beliebigen Geradenpunkt $L$ in Abhängigkeit vom Geradenparameter $r$. Wähle $r$ so, dass der Verbindungsvektor orthogonal zum Richtungsvektor der Geraden $g$ ist.

Berechne nun den Abstand $d(P,g)=d(P,L)$.

Aufgabe 7: Die richtige Reihenfolge

Im Folgenden wurde der Abstand von $A(3|9|-2)$ und $g:\vec{x}=\begin{pmatrix} 9 \\ -3 \\ 2 \end{pmatrix}+s\cdot\begin{pmatrix} 4 \\ -5 \\ -7 \end{pmatrix}$ bestimmt. Bringe die einzelnen Schritte in die richtige Reihenfolge.

Aufgabe 6: Lichterkette

Für ein Stadtfest soll von der Spitze $P(-2|3|10)$ eines Restaurants eine Lichterkette auf kürzestem Weg zur nahen Uferlinie des Kanals $g:\vec{x}=\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}+r\cdot\begin{pmatrix} -4 \\ 3 \\ 2 \end{pmatrix}$ eine Lichterkette gespannt werden.

Berechne die Mindestlänge der Lichterkette auf Meter gerundet.

Die Lichterkette muss mindestens $5,48 Meter$ lang sein.

1. Stelle die Hilfsebene $H$ in Koordinatenform auf:

$-4x_1+3x_2+2x_3=37, da \begin{pmatrix} -2 \\ 3 \\ 10 \end{pmatrix}\cdot\begin{pmatrix} -4 \\ 3 \\ 2 \end{pmatrix}=37$

1. Schnittpunkt von $g$ und $H$ bestimmen:

$-4\cdot(1-4r)+3\cdot(2+3r)+2\cdot(3+2r)=37 \Leftrightarrow -4+16r+6+9r+6+4r=37 \Leftrightarrow 8+29r=37 \Leftrightarrow 29r=29 \Leftrightarrow r=1$

1. $r$ in $g$ einsetzten, um $L$ zu bestimmen:

Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle g:\vec{x}= \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}+1\cdot\begin{pmatrix} -4 \\ 3 \\ 2 \end{pmatrix}=\begin{pmatrix} -3 \\ 5 \\ 5 \end{pmatrix } $\Rightarrow L(-3|5|5)$

1. Abstand $d(P,L)=d(P,L)$ bestimmen:

$d(P,L)=\sqrt{(-3-(-2))^2+(5-3)^2+(5+10)^2}=\sqrt{30}\approx 5,477$

Die Lichterkette muss mindestens $5,48 Meter$ lang sein.

Aufgabe 7: Dreieck

Es sind die Punkte $B(2|8|1)$ und $C(0,5|3,5|7)$ gegeben, durch sie verläuft die Gerade $g$. Die Strecke $\vec{BC}$ bildet die Grundseite eines Dreiecks mit dem dritten Punkt $A$. $A$ liegt auf der zu $g$ parallelen Geraden $j:\vec{x}= \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix}+s\cdot\begin{pmatrix} 1 \\ 3 \\ -4 \end{pmatrix}$. a) Stimmt die Behauptung "Der Flächeninhalt des Dreiecks $ABC$ ändert sich, je nachdem wo $A$ auf der Geraden $h$ liegt"? Wenn ja, warum? Wenn nein, warum nicht?

Du kannst mit der Maus den Punkt $A$ verschieben.

Überlege dir, wie man den Flächinhalt eines Dreiecks allgemein berechnet. Wie ändert sich die Höhe des Dreiecks, wenn man $A$ verschiebt?

Die Behauptung stimmt nicht. Den Flächeninhalt $F$ eines Dreiecks kann man bekanntermaßen mit der Formel $F=\frac{1}{2}\cdot G \cdot h$ berechnen, wobei $G$ die Länge der Grundseite ist.

In dieser Aufgabe bleibt der Abstand $Abst(A,g)$ immer gleich, da sich $A$ auf einer zu $g$ parallelen Geraden "bewegt". Also ist die Höhe $h$ all dieser Dreiecke gleich. Deshalb ändert sich auch der Flächeninhalt $F=\frac{1}{2}\cdot G \cdot h$ nicht.

b) Bestimme den Flächeninhalt des Dreicks $ABC$.

Überlege dir, welche Abstände du berechnen musst, um den Flächeninhalt bestimmen zu können.

Wir bestimmen zunächst die Länge $G$ der Grundseite: Es $Abst(B,C)=\sqrt((2-0,5)^2+(8-3,5)^2+(1-7)^2)=\sqrt(58,5)$.

Nun bestimmen wir die Höhe $h$, also den Abstand der parallelen Geraden $g$ und $j$ mithilfe des Verbindungsvektors von $B$ zur Geraden $j$.(Da die Geraden parallel sind, ist es natürlich egal, welche der Geraden und welchen Punkt auf der anderen Geraden man nimmt. Ihr könntet ebenso mit dem anderen Verfahren, also mit einer Hilfsebene arbeiten):

Der Punkt $L_s=(1+t|1+3t|2-4t)$ ist ein allgemeiner Punkt auf $j$. Ein allgemeiner Verbindungsvektor zwischen $B$ und $j$ ist also gegeben durch $\vec{BL_s}=\begin{pmatrix} (1+t)-2 \\ (1+3t)-8 \\ (2-4t)-1 \end{pmatrix}=\begin{pmatrix} -1+t \\ -7+3t \\ 1-4t \end{pmatrix}$. Damit $\vec{BL_s}$ orthogonal zum Richtungsvektor von $j$ ist, muss gelten: $\begin{pmatrix} -1+t \\ -7+3t \\ 1-4t \end{pmatrix}\cdot \begin{pmatrix} 1 \\ 3 \\ -4 \end{pmatrix}=0$ bzw. $(t-1)\cdot 1+(-7+3t)\cdot 3 + (1-4t) \cdot (-4)$, also $t=1$. Für $L=(2|4|-2)$ ist der Verbindungsvektor also am kürzesten. Somit ist $h=Abst(B,j)=Abst(B,L)=\sqrt((2-2)^2+(4-8)^2+(-2-1)^2)=\sqrt(25)=5$.

Der Flächeninhalt des Dreiecks beträgt also $F=\frac{1}{2}\cdot G \cdot h=\frac{1}{2}\cdot \sqrt(58,5) \cdot 5\approx 19,12$ Flächeneinheiten.

Der Flächeninhalt des Dreiecks beträgt also $19,12$ Flächeneinheiten.

Abstand zweier windschiefer Geraden

• Janne: Verfahen in richtige Reihenfolge bringen
• Janne: Merksatz

Verschiebe die Punkte $G$ und $H$ so, dass $\overline{GH}$ die kürzeste Verbindungsstrecke zwischen den windschiefen Geraden $g$ und $h$ ist.

Merke: Der Abstand windschiefer Geraden

Der Abstand zweier windschiefer Geraden $g$ und $h$ ist die kleinste Entfernung zwischen den Punkten von $g$ und den Punkten von $h$. Diese kürzeste Verbindungsstrecke $\overline{GH}$ zwischen den beiden Geraden ist sowohl orthogonal zu $g$ als auch orthogonal zu $h$ und heißt gemeinsames Lot der windschiefen Geraden $g$ und $h$.

Für die Bestimmung des Abstandes $d(g,h)$ berechnet man also die Länge des gemeinsamen Lotes der Geraden. Dafür gibt es wieder verschiedene Möglichkeiten. Hier werden zwei Verfahren noch einmal zusammengefasst: Seien $g: \vec{x}=\vec{p}+s\cdot \vec{u}$ und $h: \vec{x}=\vec{q}+t\cdot \vec{v}$ die windschiefen Geraden.

1. Verfahren (Gemeinsames Lot):

Bestimme die Geradenpunkte $G$ und $H$ in Abhängigkeit von dem jeweiligen Geradenparameter.

Stelle den Verbindungsvektor $\vec{G_s H_t}$ in Abhängigkeit von den Geradenparametern auf.

Bestimme nun die Parameter $s$ und $t$ so, dass der Verbindungsvektor $\vec{G_s H_t}$ orthogonal zu den Richtungsvektoren von $g$ und $h$ ist. Du löst also das lineare Gleichungssystem mit den beiden Gleichungen $\vec{G_s H_t}\cdot \vec{u} =0$ und $\vec{G_s H_t}\cdot \vec{v} =0$.

Mit diesen Parametern erhältst du die Lotfußpunkte $G$ und $H$ und kannst den Abstand $d(g,h)=d(G,H)$ bestimmen.

2. Verfahren (Hilfsebene):

Es gibt eine Ebene $E$, sodass $g$ in $E$ liegt und $h$ parallel zu $E$ ist. Für diese Ebene $E$ ist dann der Abstand zwischen den Geraden $d(g,h)$ gleich dem Abstand zwischen $E$ und einem beliebigen Punkt $H$ auf $h$.

Jeder Normalenvektor von dieser Ebene $E$ ist orthogonal zu den Richtungsvektoren von $g$ und $h$. Bestimme also aus den Gleichungen $\vec{u}\cdot\vec{n}=0$ und $\vec{v}\cdot\vec{n}=0$ einen Normalenvektor.

Stelle nun die Normalengleichung $(\vec{x}-\vec{p})\cdot\vec{n}=0$ der Ebene $E$ auf. Bestimme mit der Hesse´schen Normalenform oder dem Lotfußpunktverfahren (siehe Abschnitt Abstand Punkt Ebene) den Abstand $d(E,H)=d(g,h)$.

Aufgabe 7

Aufgabe 7: Maulwurf

Zwei Maulwürfe graben Tunnel mit einem Durchmesser von jeweils $5cm$. Der erste Maulwurf gräbt entlang der Geraden $g:\vec{x}=\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}+s\cdot \begin{pmatrix} -3 \\ 0 \\ 2 \end{pmatrix}$ und der zweite entlang der Geraden $h:\vec{x}=\begin{pmatrix} 6 \\ 6 \\ 18 \end{pmatrix}+t\cdot \begin{pmatrix} 3 \\ -4 \\ 1 \end{pmatrix}$ wobei diese Geraden jeweils in der Mitte des Tunnels liegen. Die Geraden schneiden sich nicht, aber ihre Tunnel sind nur stabil, wenn sie überall mindestens $20cm$ Erde dazwischen sind. Eine Längeneinheit im Koordinatensystem entspricht $1cm$. Wird das Tunnelsystem halten?

Da die Tunnel einen Radius von $2,5cm$ haben und die Geraden in dem Modell in der Mitte der jeweiligen Tunnel liegen, müssen die Geraden mindestens einen Abstand von $2,5cm+20cm+2,5cm=25cm$ haben, damit die Tunnel nicht einstürzen.

Wir bestimmen den Abstand zwischen den Geraden mit einer Hilfsebene $E$, die parallel zur Geraden $h$ ist und in der die Gerade $g$ liegt. Für den Normalenvektor $\vec{n}$ muss gelten: $\begin{pmatrix} -3 \\ 0 \\ 2 \end{pmatrix}\cdot \vec{n}$

und $\begin{pmatrix} 3 \\ -4 \\ 1 \end{pmatrix}\cdot \vec{n}$

Die Tunnel werden also einstürzen.

Dann bauen die beiden Maulwürfe an der kritischen Stelle einfach eine gemeinsame Höhle :).

Gemischte Aufgaben

• auf Anfangsaufgabe zurückkommen
• 3 Aufgaben

Wenn es geht, GeoGebra einbauen!!!