Herta-Lebenstein-Realschule/Lineare Funktionen im Aktiv-Urlaub/2.4 Anwendungen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
K (Navigation) Markierung: Quelltext-Bearbeitung 2017 |
K (LearningApp ergänzt) Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 38: | Zeile 38: | ||
4. Beziehe deine mathematische Lösung auf die Alltagssituation und formuliere einen Antwortsatz.|Merksatz}} | 4. Beziehe deine mathematische Lösung auf die Alltagssituation und formuliere einen Antwortsatz.|Merksatz}} | ||
{{Box|Übung 1: Was ist mathematisch gesucht?|Bearbeite die folgende LearningApp.|Üben}} | |||
{{LearningApp|app=psa3cgk3n21|width=100%|height=400px}} | |||
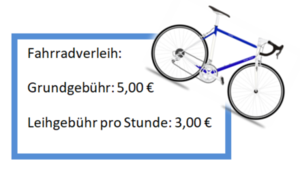
{{Box|Anwendungsaufgabe 1: Fahrradverleih|[[Datei:Fahrradverleih.png|mini]] | {{Box|Anwendungsaufgabe 1: Fahrradverleih|[[Datei:Fahrradverleih.png|mini]] | ||
Version vom 24. Mai 2021, 12:55 Uhr
Vorwissen
1 Zuordnungen und Funktionen
2 Lineare Funktionen
2.1 Lineare Funktionen erkennen und darstellen
2.2 Funktionsgleichung und Funktionsgraph
2.3 Wertetabelle und Funktionsgleichung
2.4 Lineare Funktionen im Aktivurlaub und andere Anwendungen
Es gibt Situationen in unserem Alltag, in denen sich Probleme oder Fragen mithilfe von linearen Funktionen beschreiben und lösen lassen. Solche Aufgaben nennen wir "Anwendungsaufgaben". Die Alltagssituation wird in ein mathematisches Modell übertragen, mit unserem Wissen zu den linearen Funktionen mathematisch gelöst und diese Lösung dann auf die Situation bezogen. Die nachfolgende Struktur hilft dir dabei:
Die Zuordnung lautet Zeit [Stunden] Kosten [€]
x gibt also die Zeit an, f(x) die Kosten.
Du leihst das Fahrrad für 3 Stunden, also ist x=3. Setze in der Funktionsgleichung für x die Zahl 3 ein und berechne f(3).
Verbergen