Benutzer:Buss-Haskert/Trigonometrie/Berechnungen in allgemeinen Dreiecken: Unterschied zwischen den Versionen
K (weiterlink) Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 211: | Zeile 211: | ||
Du merkst, es kommt zu Rundungsungenauigkeiten.<br> | Du merkst, es kommt zu Rundungsungenauigkeiten.<br> | ||
=== 3.3 Beispiel 3: Zwei Seiten und ein anliegender Winkel sind gegeben === | ===3.3 Beispiel 3: Zwei Seiten und ein anliegender Winkel sind gegeben=== | ||
NOCH ERGÄNZEN (nur eine Höhe ist möglich) | NOCH ERGÄNZEN (nur eine Höhe ist möglich) | ||
<br> | <br> | ||
| Zeile 229: | Zeile 229: | ||
{{Lösung versteckt|Löse wie im 3. Beispiel, es sind zwei Seiten und ein anliegender Winkel gegeben|Tipp zu Nr. 4|Verbergen}} | {{Lösung versteckt|Löse wie im 3. Beispiel, es sind zwei Seiten und ein anliegender Winkel gegeben|Tipp zu Nr. 4|Verbergen}} | ||
=== 3.4 Anwendungsaufgaben === | ===3.4 Anwendungsaufgaben=== | ||
{{Box|Übung 3 (online und im Heft)|Löse auf der Seite [https://www.aufgabenfuchs.de/mathematik/flaeche/dreieck/trigonometrie.shtml '''Aufgabenfuchs'''] die folgenden Aufgaben. Notiere zu jeder Aufgabe eine Lösung ausführlich mit Skizze und Rechnung in deinem Heft. | |||
* 63 | |||
* 64|Üben}} | |||
{{Box|Übung | {{Box|Übung 4|Löse die Aufgaben aus dem Buch. Zeichne die Skizzen in dein Heft und löse schrittweise. Notiere vollständig und übersichtlich. | ||
* S. 99 Nr. 5 | * S. 99 Nr. 5 | ||
* S. 100 Nr. 7 | * S. 100 Nr. 7 | ||
* S. 100 Nr. 8|Üben}} | * S. 100 Nr. 8|Üben}} | ||
=== 3.5 Formel für den Flächeninhalt beliebiger Dreiecke === | ===3.5 Formel für den Flächeninhalt beliebiger Dreiecke=== | ||
EVENTUELL ODER ALS ZUSATZ | EVENTUELL ODER ALS ZUSATZ | ||
{{Fortsetzung|weiter=4 Berechnungen in beliebigen Figuren|weiterlink=Benutzer:Buss-Haskert/Trigonometrie/Berechnungen in beliebigen Figuren}} | {{Fortsetzung|weiter=4 Berechnungen in beliebigen Figuren|weiterlink=Benutzer:Buss-Haskert/Trigonometrie/Berechnungen in beliebigen Figuren}} | ||
Version vom 8. März 2021, 18:41 Uhr
SEITE IM AUFBAU
1) Sinus, Kosinus, Tangens
2) Strecken- und Winkelberechnungen in rechtwinkligen Dreiecken
3 Strecken- und Winkelberechnungen in allgemeinen Dreiecken
Die Seitenverhältnisse Sinus, Kosinus und Tanges gelten nur für rechtwinklige Dreiecke.
Um in allgemeinen Dreiecken Strecken und Winkel berechnen zu können, zerlege das Dreieck mithilfe einer Höhe in zwei rechtwinklige Dreiecke.
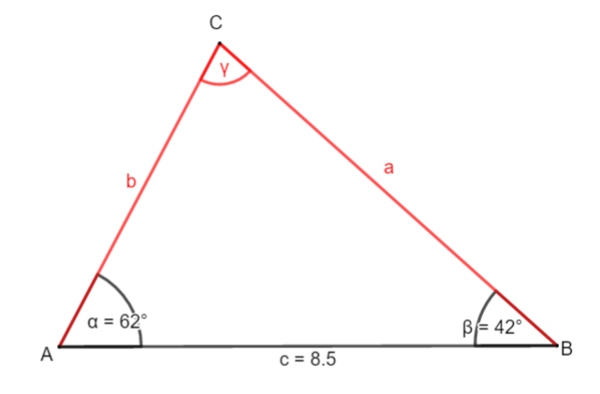
3.1 Beispiel 1: Eine Seite und zwei Winkel sind gegeben
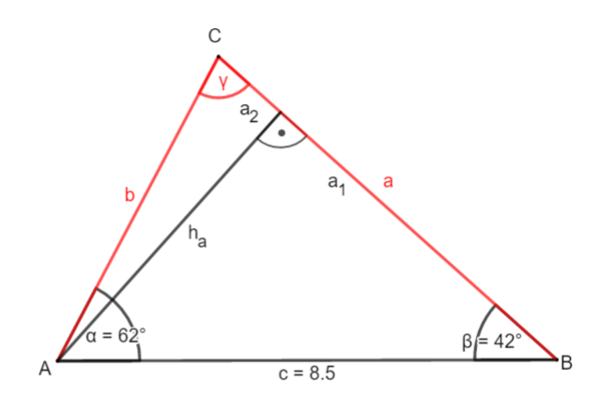
1. Möglichkeit: Zerlege das Dreieck durch die Höhe ha ein zwei rechtwinklige Dreiecke.
① Bestimme γ:
Winkelsummensatz
γ = 180° - α - β
= 180° - 42° - 62°
= 76°
② Berechne ha:
sin β = | ·c
c · sin β = ha
8,5 · sin(42°) = ha
5,7 (cm) ha
③ Berechne b:
sin γ = | ·b
b · sin γ = ha | : sin γ
b =
b =
b 5,9 (cm)
④ Berechne a:
cos β = | ·c
c · cos β = a1
8,5 · cos (42°) = a1
cos γ = | ·c
b · cos γ = a2
5,9 · cos (76°) = a2
= 6,3 + 1,4
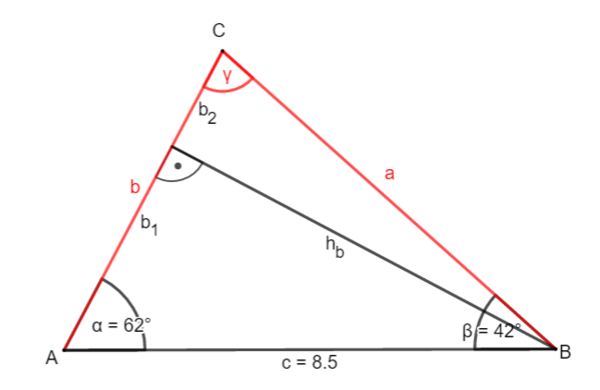
2. Möglichkeit: Zerlege das Dreieck durch die Höhe hb ein zwei rechtwinklige Dreiecke.
① Bestimme γ:
Winkelsummensatz
γ = 180° - α - β
= 180° - 42° - 62°
= 76°
② Berechne hb:
sin α = | ·c
c · sin α = hb
8,5 · sin(62°) = hb
7,5 (cm) hb
③ Berechne a:
sin γ = | ·a
a · sin γ = hb | : sin γ
a =
a =
a 7,7 (cm)
④ Berechne b:
cos α = | ·c
c · cos α = b1
8,5 · cos (62°) = b1
cos γ = | ·c
a · cos γ = b2
7,7 · cos (76°) = b2
= 4,0 + 1,9
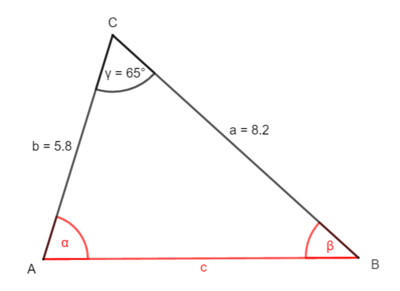
3.2 Beispiel 2: Zwei Seiten und der eingeschlossene Winkel sind gegeben
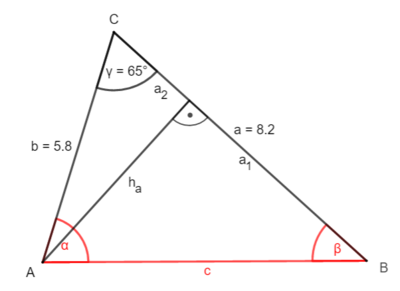
1. Möglichkeit: Zerlege das Dreieck durch die Höhe ha ein zwei rechtwinklige Dreiecke.
① Bestimme ha:
sin γ = |·b
b · sin γ = ha
5,8 · sin(65°) = ha
5,2 (cm) ha
② Bestimme a2
cos γ = |·b
b · cos γ = a2
5,8 · cos(65°) = a2
2,5 (cm) a2
③ Bestimme a1
a – a2= a1
8,2 - 3,8 = a1
5,7 (cm) = a1
④ Bestimme β
tan β =
tan β = |tan-1
β 42,4°
⑤ Bestimme c
sin β = |·c
c · sin β = ha |: sin β
c =
c =
c=
c =
c 7,7 (cm)
⑥ Bestimme den letzten Winkel α
Winkelsumme
α + β + γ = 180° |- β; -γ
α = 180° - β - γ
α = 180° - 42,4° - 65°
α = 72,6°
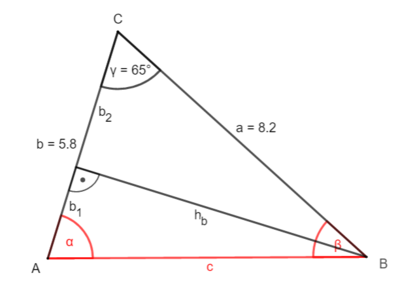
2. Möglichkeit: Zerlege das Dreieck durch die Höhe hb ein zwei rechtwinklige Dreiecke.
① Bestimme hb:
sin γ = |·a
a · sin γ = hb
8,2 · sin(65°) = hb
7,4 (cm) hb
② Bestimme b2
cos γ = |·a
a · cos γ = b2
8,2 · cos(65°) = b2
3,5 (cm) b2
③ Bestimme b1
b – b2= b1
5,8 - 3,5 = b1
2,3 (cm) = b1
④ Bestimme α
tan α =
tan α = |tan-1
α 72,7°
⑤ Bestimme c
sin α = |·c
c · sin α = hb |: sin α
c =
c =
c=
c =
c 7,7 (cm)
⑥ Bestimme den letzten Winkel β
Winkelsumme
α + β + γ = 180° |- α; -γ
β = 180° - α - γ
β= 180° - 72,7° - 65°
β = 42,3°
Du merkst, es kommt zu Rundungsungenauigkeiten.
3.3 Beispiel 3: Zwei Seiten und ein anliegender Winkel sind gegeben
NOCH ERGÄNZEN (nur eine Höhe ist möglich)
3.4 Anwendungsaufgaben
3.5 Formel für den Flächeninhalt beliebiger Dreiecke
EVENTUELL ODER ALS ZUSATZ