Digitale Werkzeuge in der Schule/Fit für VERA-8/Zinsrechnung/Zinseszins: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 211: | Zeile 211: | ||
{{Box | Aufgabe 4: Coronabonus | | |||
Detlef arbeitet als Krankenpfleger. Daher hat er einen Corona-Bonus von <math>1000\euro</math> erhalten. Seine Frau ist Professorin, deshalb sind sie als Familie finanziell gut abgesichert. Er möchte deswegen <math>800\euro</math> des Corona-Bonuses sparen. | |||
'''a)''' Seine Bankberaterin bei der SparBank sagt ihm: "Bei uns bekommen Sie so viel Zinsen, dass Sie nach vier Jahren schon ungefähr 136 Euro mehr haben." Wie hoch liegt der Zinssatz bei der SparBank? | '''a)''' Seine Bankberaterin bei der SparBank sagt ihm: "Bei uns bekommen Sie so viel Zinsen, dass Sie nach vier Jahren schon ungefähr 136 Euro mehr haben." Wie hoch liegt der Zinssatz bei der SparBank? | ||
| Zeile 230: | Zeile 231: | ||
{{Lösung versteckt|1= Mögliche Rechnung: <math>(800+x)\cdot(1 + 1\cdot \frac{4}{100})^4= 1170</math> | {{Lösung versteckt|1= Mögliche Rechnung: <math>(800+x)\cdot(1 + 1\cdot \frac{4}{100})^4= 1170</math> | ||
umstellen nach <math>x</math>: <math>(800+x)= 1170:(1 + 1\cdot \frac{4}{100})^4</math> | umstellen nach <math>x</math>: <math>(800+x)= 1170:(1 + 1\cdot \frac{4}{100})^4</math> | ||
Daraus folgt <math>x= 1170:(1 + 1\cdot \frac{4}{100})^4-800=200{,}121</math> | Daraus folgt <math>x= 1170:(1 + 1\cdot \frac{4}{100})^4-800=200{,}121</math> | ||
| Zeile 242: | Zeile 242: | ||
{{Lösung versteckt|1= Es gibt nicht die eine richtige Lösung. Hier sind einige mögliche Argumente, aber du hast vielleicht auch andere gute Argumente gefunden: | {{Lösung versteckt|1= Es gibt nicht die eine richtige Lösung. Hier sind einige mögliche Argumente, aber du hast vielleicht auch andere gute Argumente gefunden: | ||
Bei zwei Prozent Zinsen halbjährlich ist Detlef am flexibelsten, da er nicht ein ganzes bzw. fünf Jahre warten muss um die Zinsen zu bekommen. | Bei zwei Prozent Zinsen halbjährlich ist Detlef am flexibelsten, da er nicht ein ganzes bzw. fünf Jahre warten muss um die Zinsen zu bekommen. | ||
Bei zwei Prozent Zinsen alle 6 Monate bekommt er mehr Geld als bei vier Prozent Zinsen jährlich, weil er dann jedes Jahr zwei mal zwei Prozent (also vier Prozent) auf sein Startkapital und dazu am Ende des Jahres schon die die Zinseszinsen des ersten Halbjahres bekommt. | Bei zwei Prozent Zinsen alle 6 Monate bekommt er mehr Geld als bei vier Prozent Zinsen jährlich, weil er dann jedes Jahr zwei mal zwei Prozent (also vier Prozent) auf sein Startkapital und dazu am Ende des Jahres schon die die Zinseszinsen des ersten Halbjahres bekommt. | ||
Rechnerischer Vergleich nach fünf Jahren: | Rechnerischer Vergleich nach fünf Jahren: | ||
SparBank:<math>1000\cdot(1 + 1\cdot \frac{4}{100})^5= 1216{,}65</math> | SparBank:<math>1000\cdot(1 + 1\cdot \frac{4}{100})^5= 1216{,}65</math> | ||
| Zeile 263: | Zeile 260: | ||
nach zwei Jahren: <math>(1227{,}2+15\cdot 12)\cdot\left(1 + 1\cdot \frac{4}{100}\right)= 1463{,}49</math> | nach zwei Jahren: <math>(1227{,}2+15\cdot 12)\cdot\left(1 + 1\cdot \frac{4}{100}\right)= 1463{,}49</math> | ||
nach drei Jahren: <math>(1463{,}49+15\cdot 12)\cdot\left(1 + 1\cdot \frac{4}{100}\right)= 1709{,}23</math> | nach drei Jahren: <math>(1463{,}49+15\cdot 12)\cdot\left(1 + 1\cdot \frac{4}{100}\right)= 1709{,}23</math> | ||
Detlef hat nach drei Jahren mit der Lohnerhöhung <math>1709{,}23</math> € auf seinem Konto | Detlef hat nach drei Jahren mit der Lohnerhöhung <math>1709{,}23</math> € auf seinem Konto | ||
|2=Lösung zu 4 d)|3=Einklappen}} | |2=Lösung zu 4 d)|3=Einklappen}} | ||
| Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | | Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | ||
Version vom 26. November 2020, 16:07 Uhr
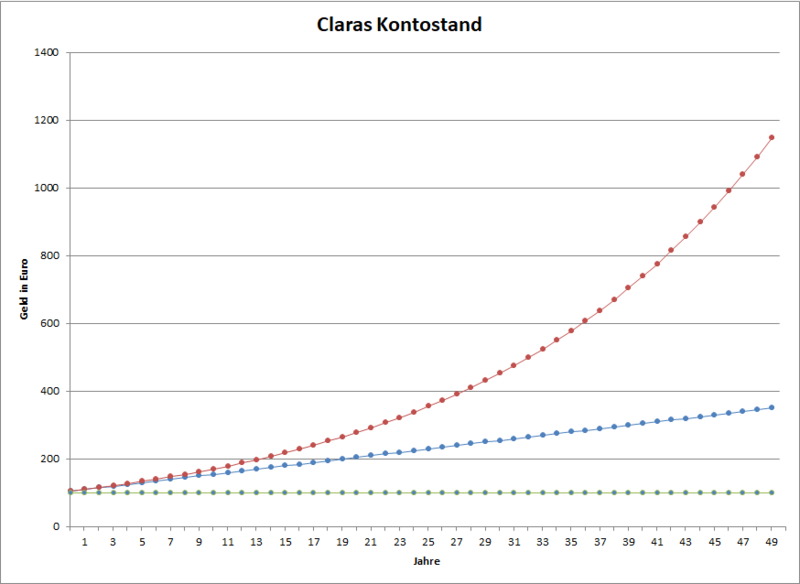
| roter Graph | Entwicklung mit Zinseszins |
| blauer Graph | Entwicklung mit Zinsen ohne Zinseszins |
| grüner Graph | Entwicklung ohne Zinsen |
Hier gibt es kein richtig oder falsch. Dir ist bestimmt viel Unterschiedliches aufgefallen.
Hier sind nur einige Auffälligkeiten:
Am Anfang sind der rote und der blaue Graph fast gleich, erst ab etwa Jahren gibt es nennenswerte Unterschiede. Das bedeutet, dass es für die ersten Jahre fast keinen Unterschied macht, ob Clara Zinseszins bekommt oder nur einfache Zinsen.
Ab Jahren wird der Unterschied zwischen dem blauen und den roten Graphen immer größer. Das bedeutet, dass es langfristig einen erheblichen Unterschied macht, ob Clara Zinseszins bekommt oder nur einfachen Zins.
Der Unterschied zwischen dem blauen und roten Graphen wird mit den Jahren immer schneller größer. Das bedeutet: Je länger Clara spart, desto mehr Gewicht hat der Zinseszins gegenüber dem einfachen Zins.| Arbeitsmethode | Farbe=#F19D50 }}
Link zum nächsten Kapitel:
Digitale Werkzeuge in der Schule/Fit für VERA-8/Zinsrechnung/Abschlussvideo
Link zurück zur Übersicht:
Digitale Werkzeuge in der Schule/Fit für VERA-8/Zinsrechnung