Benutzer:Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
K (Übungen und Lösungen ergänzt) Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 10: | Zeile 10: | ||
Info: Übungen befinden sich auf der Seite Aufgabenfuchs Nr. 1-36 [https://mathe.aufgabenfuchs.de/flaeche/einfache-flaechen.shtml] | Info: Übungen befinden sich auf der Seite Aufgabenfuchs Nr. 1-36 [https://mathe.aufgabenfuchs.de/flaeche/einfache-flaechen.shtml] | ||
===4.1) Quadrat: Umfang und Flächeninhalt=== | ===4.1) Quadrat und Rechteck: Umfang und Flächeninhalt=== | ||
{{Box|Quadrat und Rechteck|Stelle beim nachfolgenden GeoGebra-Applet mithilfe der Schieberegler die Länge und Breite so ein, dass du zunächst ein Quadrat betrachtest!<br> Wiederhole: Wie kannst du den Flächeninhalt berechnen?<br> | |||
Stelle danach verschiedene Rechtecke ein.<br> Wiederhole: Wie kannst du den Flächeninhalt berechnen?|Lösung|Icon=brainy hdg-scientist07}} | |||
<ggb_applet id="FexywbYW" width="800" height="600" /> | |||
{{Box|Umfang und Flächeninhalt von Quadrat und Rechteck|Bearbeite das nachfolgende Quiz und übertrage den Merksatz anschließend in dein Heft. Denke an die passenden Skizzen. <br>Notiere die Formeln auch in deinem Heft der Vierecke.|Arbeitsmethode}} | |||
<div class="lueckentext-quiz"> | |||
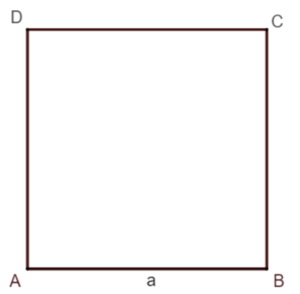
[[Datei:Quadrat allgemein.png|mini]] | |||
QUADRAT<br> | |||
Flächeninhalt A = '''a∙a''' <br>= '''a²'''<br> | |||
Umfang u = '''4∙a''' | |||
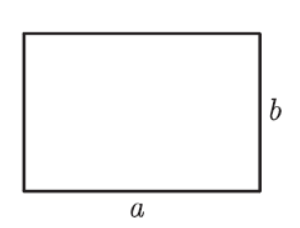
[[Datei:Rechteck allgemein.png|mini]] | |||
RECHTECK | |||
Flächeninhalt A= '''a∙b''' <br> | |||
Umfang u = 2a + 2b = '''2(a+b)''' . | |||
</div> | |||
{{Box|Übung 1|Löse S. 83 Nr. 4 und 5.|Üben}} | |||
{{Lösung versteckt|1=Da die Seitenlänge gesucht ist, musst du die Formel umstellen:<br> | |||
u = 4∙a |:4<br> | |||
<math>\tfrac{u}{4}</math> = a<br>.<br>Setze nun die Zahlen ein und berechne.<br> | |||
a) a = 6,4cm : 4 = 1,8 cm.|2=Tipp zu Nr. 4a|3=Verbergen}} | |||
{{Lösung versteckt|1=Da die Seitenlänge gesucht ist, musst du die Formel umstellen:<br> | |||
A = a∙a |Welche Zahl mit sich selbst multipliziert ergibt also 36? <br> | |||
Erinnerung: Quadratzahlen! | |||
|2=Tipp zu Nr. 4b|3=Verbergen}} | |||
{{Lösung versteckt|1=Da die Seitenlänge b gesucht ist, musst du die Formel umstellen:<br> | |||
A = a∙b |:a | |||
<math>\tfrac{A}{a}</math> = b<br> | |||
Setze nun die Zahlen ein und berechne.<br> | |||
b = 40 : 5 = 8 (cm)|2=Tipp zu Nr. 5a|3=Verbergen}} | |||
{{Lösung versteckt|1=Da die Seitenlänge b gesucht ist, musst du die Formel umstellen:<br> | |||
u = 2∙(a + b) |:2<br> | |||
<math>\tfrac{u}{2}</math> = a + b |-a<br> | |||
<math>\tfrac{u}{2}</math> - a = b .<br>Setze nun die Zahlen ein und berechne.<br> | |||
b =<math>\tfrac{36,8}{2}</math> - 12,8= 18,4 - 12,8 = 5,6 .<br>Berechne nun den Flächeninhalt A.|2=Tipp zu Nr. 5c|3=Verbergen}} | |||
===4.3) Parallelogramm: Umfang und Flächeninhalt=== | ===4.3) Parallelogramm: Umfang und Flächeninhalt=== | ||
Version vom 4. Oktober 2020, 17:12 Uhr
4) Umfang und Flächeninhalt von Vierecken und Dreiecken
In diesem Kapitel leitest du die Formeln für den Umfang und den Flächeninhalt für die besonderen Vierecke und für Dreiecke her. Notiere alle Formeln in deinem Heft der Vierecke.
Beginne mit der Wiederholung der Formeln für das Quadrat und Rechteck.
Info: Übungen befinden sich auf der Seite Aufgabenfuchs Nr. 1-36 [1]
4.1) Quadrat und Rechteck: Umfang und Flächeninhalt

QUADRAT
Flächeninhalt A = a∙a
= a²
Umfang u = 4∙a
RECHTECK
Flächeninhalt A= a∙b
Umfang u = 2a + 2b = 2(a+b) .
Da die Seitenlänge gesucht ist, musst du die Formel umstellen:
Welche Zahl mit sich selbst multipliziert ergibt also 36?
Erinnerung: Quadratzahlen!
Da die Seitenlänge b gesucht ist, musst du die Formel umstellen:
Da die Seitenlänge b gesucht ist, musst du die Formel umstellen: