Digitale Werkzeuge in der Schule/Basiswissen Analysis/Steckbriefaufgaben

Allgemeine Hinweise

Lernpfad: Steckbriefaufgaben

Auf dieser Seite lernst Du Steckbriefaufgaben kennen. In Steckbriefaufgaben geht es darum, aus den Eigenschaften einer Funktion deren Funktionsterm und deren Funktionsgraphen herzuleiten. Dazu ist das Lösen von Gleichungssystemen mit mehr als einer Variablen notwendig, was Du auf dieser Seite lernen wirst.

Wie empfehlen Dir, Dich bereits mit den Eigenschaften von Funktionen und der lokalen Änderungsrate beschäftigt zu haben, wenn Du mit dieser Seite beginnst.

In diesem Lernpfadkapitel kannst du ... Lernziele

• In Aufgaben, die gelb gefärbt sind, kannst du Gelerntes wiederholen und vertiefen.

• Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit.

• Und Aufgaben mit grüner Hinterlegung sind Knobelaufgaben.

Eigenschaften von Ganzrationalen Funktionen

Baustelle

An diesem Abschnitt wird aktuell noch gearbeitet. Fahre zunächst bei dem Lösen von Gleichungssystemen weiter unten fort.

In diesem Abschnitt werden wir kurz die Eigenschaften von Ganzrationalen Funktionen wiederholen. Solltest Du das Kapitel Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung noch nicht bearbeitet haben, empfehlen wir Dir, Dich zuerst damit vertraut zu machen. Wenn Du Dich fit fühlst beim Thema Funktionseigenschaften, kannst Du die Wiederholung überspringen und Dein Wissen im Quiz im unteren Bereich dieses Abschnitts testen.

Definition: Ganzrationale Funktionen

Eine Ganzrationale Funktion nennt man auch Polynomfunktion oder kurz Polynom.

Beispiele sind:

$f(x)=3x^4-2x^2+7$

$f(x)=-10x^3-9x^2+x$

Ganzrationale Funktionen sind Summen von Potenzfunktionen. Die Zahlen mit denen einzelne Potenzfunktionen multipliziert werden, nennt man Koeffizienten. Den Wert des größten Exponenten nennt man den Grad der Funktion.

Die Koeffizienten des ersten Beispiels sind $3$, $-2$ und $7$. Der Grad ist $4$, sodass man sagt, die es handelt sich um eine Funktion $4.$ Grades.

Schnittpunkte

Scheidet eine Funktion $f(x)$ die y-Achse, so liegt ein Punkt $P_y(0|y_s)$, dessen x-Wert gleich $0$ ist, auf dem Funktionsgraphen.

Für den Funktionsterm gilt entsprechend $f(0)=y_s$

$f(x)=2x^3+3x+4$

$\Rightarrow f(0)=2 \cdot 0^3+3 \cdot 0+4=4$

$\Rightarrow P_y(0|4)$

Die $y$-Koordinate von $P_y$ ist immer gleich dem letzten Koeffizienten, welcher nicht mit $x$ multipliziert wird. Sie lässt sich also immer aus der Funktionsgleichung ablesen.

Scheidet eine Funktion $f(x)$ die x-Achse, so liegt ein Punkt $P_x(x_s|0)$, dessen y-Wert gleich $0$ ist, auf dem Funktionsgraphen. Man bezeichnet einen Schnittpunkt mit der x-Achse in der Regel als Nullstelle.

Ganzrationale Funktionen können mehr als eine Nullstelle haben. Um genau zu sein, kein eine ganzrationale Funktion maximal so viele Nullstellen haben, wie der Wert ihres Grades beträgt. Ist ihr Grad außerdem ungerade, so haben sie mindestens eine Nullstelle.

Um die Nullstellen einer Funktion $f(x)$ zu berechnen, setzt du den Funktionsterm $=0$ und löst die Gleichung nach $x$ auf. Verfahren zur Lösung, die Du kennen könntest, sind die pq-Formel, das Faktorisierungsverfahren, das Substitutuionsverfahren oder die Polynomdivision.

$f(x)=3x^2-9x-12=0$ $\mid :3$

$\Leftrightarrow x^2-3x-4=0$

$p=-3$ , $q=-4$

$x_{1/2}=- \frac{p}{2} \pm \sqrt{( \frac{p}{2} )^2 -q}$

$x_{1/2}=- \frac{-3}{2} \pm \sqrt{( \frac{-3}{2})^2-(-4)}$

$x_{1/2}=1,5 \pm \sqrt{6,25}$

$x_{1/2}=1,5 \pm 2,5$

$x_1=4$ , $x_2=-1$

$f(x)=x^3-4x^2+4x=0$

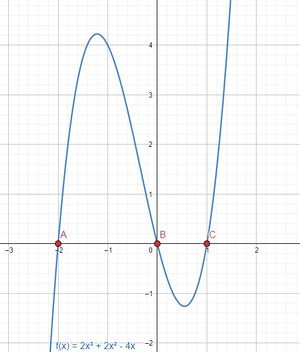
Der Faktor $x$ kann ausgeklammert werden.

$\Leftrightarrow x \cdot (x^2-4x+4)=0$

$\Rightarrow x_1 = 0$ ist die erste Nullstelle. Weitere Nullstellen ergeben sich, wenn der Ausdruck in den Klammern $=0$ wird.

$\Rightarrow x^2-4x+4=0$

$\Rightarrow x_{2/3}=- \frac{-4}{2} \pm \sqrt{( \frac{-4}{2} )^2 -4}$

$\Rightarrow x_2=2$

Die Nullstellen sind $x_1=0$ und $x_2=2$

Monotonie

Das Monotonieverhalten einer Funktion beschreibt den Verlauf des Graphen einer Funktion. Die Montonie gibt an, ob eine Funktion fällt, steigt oder konstant ist.

Symmetrie

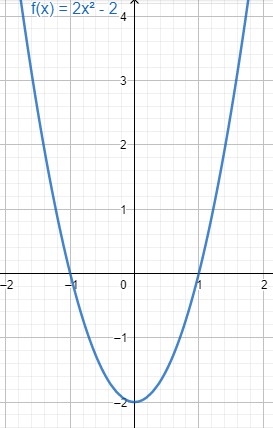
Ist eine Funktion achsensymmetrisch, so spiegelt sich der Funktionsgraph an der y-Achse. Der Graph einer ganzrationalen Funktion ist genau dann achsensymmetrisch, wenn die Funktionsgleichung nur aus geraden Exponenten besteht. Außerdem gilt für achsensymmetrische Funktionen $f(-x)=f(x)$.

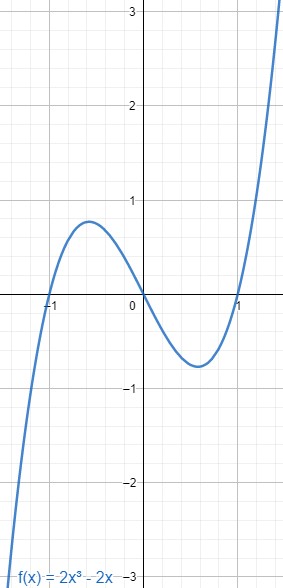
Ist eine Funktion punktsymmetrisch, so wird eine Hälfte des Graphen am Koordinatenursprung auf die andere gespiegelt wird. Der Graph einer ganzrationalen Funktion ist genau dann punktsymmetrisch, wenn die Funktionsgleichung nur aus ungeraden Exponenten besteht. Außerdem gilt für punktsymmetrische Funktionen $f(-x)=-f(x)$.

Extrema und Wendestellen

Mit einem Extremwert bezeichnet man ein lokales oder globales Maximum (Hochpunkt) oder Minimum (Tiefpunkt). Nimmt der Funktionswert $f(x)$ an einer Stelle $x$ den größten bzw. kleinsten Wert innerhalb eines Intervalles um $x$ an, so spricht man von einem lokalen Maximum bzw. lokalem Minimum. Ist der Funktionswert bei $x$ der größte bzw. kleinste Wert für den gesamten Definitionsbereich der Funktion, so nennt man ihn globales Maximum bzw. globales Minimum.

Ist $f(x)$ eine Extremstelle, so spricht man auch von einer Extremstelle der Funktion $f$ bei $x$.

Bei der Berechnung von Extremstellen einer Funktion $f(x)$ macht man sich die Eigenschaften der Ableitung $f'(x)$ zu Nutze: Eine Tangente, die an einer Extremstelle $x_1$ angelegt wird, ist parallel zur $x$-Achse. Die Steigung ist also $0$. Die Ableitung $f'(x_1)$ an dieser Stelle ist folglich $=0$.

Für alle Extremstellen $x_n$ gilt:

$f'(x_n)=0$

Das ist die Notwendige Bedingung.

Will man nun prüfen, ob es sich um ein Maximum oder um ein Minimum handelt, zieht man die zweite Ableitung $f''(x)$ hinzu.

Das Hinreichende Kriterium lautet:

• $f''(x)<0 \Rightarrow$ Es liegt ein Maximum vor.

• $f''(x)>0 \Rightarrow$ Es liegt ein Minimum vor.

Mit einem Wendepunkt bezeichnet meine eine Stelle des Funktionsgraphen, an der sich das Krümmungsverhalten des Graphen ändert. Das kann ein Wechsel von einer Rechts- zu einer Linkskurve oder von einer Links- zu einer Rechtskurve sein.

Krümmungsverhalten der Funktion sin(2x). Die Tangente ist blau gefärbt in konvexen Bereichen (Linkskurve), grün gefärbt in konkaven Bereichen (Rechtskurve) und rot gefärbt bei Wendepunkten.

Funktionsgleichung aufstellen

Bei dem Aufstellen einer Funktionsgleichung für eine ganzrationale Funktion geht es darum, die Werte aller Koeffizienten herauszufinden. Das Vorgehen ist vergleichbar mit einem Puzzle: Verschiedene Informationen über die Funktion sind Dir bekannt, die Schwierigkeit besteht nun darin, diese Informationen zu sortieren.

Der erste Schritt ist immer, beim Rahmen anzufangen. Welche Form wird der Funktionsterm haben? Handelt es sich beispielsweise um eine Funktion 2. Grades, so hat der Term die Form $f(x)=ax^2+bx+c$ mit den drei unbekannten Koeffizienten $a$, $b$ und $c$. Eine Funktion 3. Grades hätte die Form $f(x)=ax^3+bx^2+cx+d$. Und so weiter.

Als nächstes können Dir Informationen über die Symmetrie helfen. Falls die Funktion achsensymmetrisch ist, weißt Du, dass alle Koeffizienten vor ungeraden Exponenten gleich $0$ sind. Im Fall von Punktsymmetrie sind alle Koeffizienten vor geraden Exponenten gleich $0$.

Dein nächstes Ziel ist es verschiedene Gleichungen, die die unbekannten Koeffizienten enthalten aufzustellen. Wie Du ein solches System aus Gleichungen dann auflöst zeigen wir Dir unten.

Um aber zuerst Gleichungen zu erhalten, setzt du $x$- und $y$-Koordinaten von bekannten Punkten des Graphen in Deinen Rahmen ein. Wenn Du spezielle Informationen über Extremstellen, Wendepunkte oder die Ableitung allgemein hast, musst Du diese Koordinaten in den Rahmen der Ableitung der Funktion einsetzen. Diesen berechnest Du aus den bekannten Ableitungsregeln:

Sei die gesuchte Funktion vom 3. Grad.

Rahmen: $f(x)=ax^3+bx^2+cx+d$

1. Ableitung des Rahmens: $f(x)=3ax^2+2bx+c$

2. Ableitung des Rahmens: $f(x)=6ax+2b$

Funktionsgraphen zeichnen

Um den Funktionsgraphen zu zeichnen benötigst Du möglichst viele Informationen über den Graphen. Besonders hilfreiche Informationen sind Achsenschnittpunkte sowie Nullstellen, Extremstellen und Wendestellen. Kennst du den Funktionsterm kannst Du mit einer Wertetabelle darüber hinaus weitere Punkte errechnen, die auf dem Graphen liegen müssen.

Einführung

Auf dieser Seite lernst Du, wie Du Gleichungssysteme mit mehr als einer Variablen lösen kannst. Falls Du dir noch unsicher bist, wie man eine Gleichung mit nur einer Variable löst, versuche folgendes Beispiel zu lösen. Falls Du das aber noch kannst, dann überspringe das Beispiel gerne.

Beispiel

Löse folgende Gleichung: $6x-5=37$

Bringe zuerst die Variable alleine auf eine Seite und Teile dann durch die Anzahl der Variable.

$x=7$

Das Einsetzungsverfahren

Das Einsetzungsverfahren

Das Einsetzungsverfahren verwendest du, um ein Gleichungssystem mit zwei Variablen zu lösen. Dabei versuchst du zuerst eine Variable allein auf eine Seite zu bringen und diese Gleichung dann in die zweite Gleichung einzusetzen.

Schau dir folgendes Gleichungssystem an:

$\begin{array}{rlll} &I\quad& &3x& + &5y& &=& &58&\\ &II\quad& &x& + &2& &=& &y& \\ \end{array}$

Die Gleichung $II$ ist bereits nach der Variable $y$ aufgelöst. Diese fügen wir nun statt $y$ in die die Gleichung $I$ ein. Das sieht folgendermaßen aus:

$3x + 5 \cdot (x + 2) = 58$

1. Wir vereinfachen

$3x + 5x + 10 = 58$

2. Und stellen nach $x$ um

$8x = 48$

3. Dann teilen wir durch die Anzahl der Variable, hier 8 und es ergibt sich

$x = 6$

4. Das können wir nun in eine der beiden Gleichungen einsetzen und nach $y$ umstellen. Gleichung $II$ eignet sich dafür natürlich am besten. Es gilt:

$\begin{array}{rlll} &II\quad&&& x + 2 &=& y &\mid x = 6 \, \textrm{einsetzen} \\ &&&\Rightarrow& 6 + 2 &=& y \\ &&&\Rightarrow& y &=& 8 \\ \end{array}$

Merke

Du verwendest dieses Verfahren bei Gleichungssystemen mit 2 Variablen. Dabei stellst du die eine Gleichung nach einer Variable um und setzt diese dann in die andere Gleichung ein. Nun kannst du vorgehen wie bei einer Gleichung mit nur einer Variable.

Aufgaben zum Einsetzungsverfahren

Gleichungssysteme mit dem Einsetzungsverfahren lösen.

Die Schwierigkeit der Aufgaben steigt von oben nach unten.

a)

$\begin{array}{rlll} &I\quad& &7x& + &3y& &=& &50&\\ &II\quad& && &18y& &=& &6& \\ \end{array}$

$x=7$,$y=1/3$

b)

$\begin{array}{rlll} &I\quad& &3x& + &6y& &=& &6&\\ &II\quad& &-2x& + &12y& &=& &0& \\ \end{array}$

Eliminiere die $y$-Variable in der unteren Zeile.

$x=3/2$,$y=1/4$

Quadratische Funktionen im Sachzusammenhang

Aufgabe: Elternsprechtag

Jedes halbe Jahr veranstaltet eine Schule einen Elternsprechtag von 12 Uhr bis 18 Uhr. Den Eltern stehen auf dem Lehrerparkplatz aber nur eine begrenzte Anzahl an Parkplätzen zur Verfügung, sodass die Schulleitung rechtzeitig entscheiden muss, ob noch weitere Parkplätze angemietet werden müssen. Sie geht davon aus, dass der erste Parkplatz erst nach Beginn des Elternsprechtages belegt wird und spätestens um 18 Uhr das letzte Auto den Parkplatz verlassen hat. Diesen Elternsprechtag stehen den Eltern 50 Parkplätze zur Verfügung. Eine Zählung um 13 Uhr ergibt, dass bereits die Hälfte der zur Verfügung stehenden Parkplätze belegt ist.

a)

Die Anzahl belegter Parkplätze lässt sich in Abhängigkeit zur Uhrzeit (mit $t$ in Stunden, wobei $t = 0$ 12 Uhr repräsentiert) durch eine quadratische Funktion der Form $f(t) = at^2 + bt + c$ beschreiben. Löse zunächst unteren Lückentext und stelle dann mit dessen Hilfe die Gleichung von $f$ auf. Indem du die Box "Funktionsgleichung überprüfen" öffnest, kannst du dein Ergebnis selbstständig überprüfen.

$f(t) = -5t^2 + 30t$

$\begin{array}{rlll} f(t) &=& at^2 + bt + c \\ \end{array}$



$\begin{array}{rlll} &&f(0) &=& 0 \\ &\Leftrightarrow& a \cdot 0^2 + b \cdot 0 + c &=& 0 \\ &\Leftrightarrow& c &=& 0 \\ \end{array}$



$\Rightarrow f(t) = at^2 + bt$



$\begin{array}{rlll} &&f(1) &=& 25 \\ &\Leftrightarrow& a \cdot 1^2 + b \cdot 1 &=& 25 \\ &\Leftrightarrow& a + b &=& 25 \\ \end{array}$



$\begin{array}{rlll} &&f(6) &=& 0 \\ &\Leftrightarrow& a \cdot 6^2 + b \cdot 6 &=& 0 \\ &\Leftrightarrow& 36a + 6b &=& 0 \\ \end{array}$





Insgesamt erhalten wir also folgendes Gleichungssystem:

$\begin{array}{rlll} &I\quad& a + b &=& 25 \\ &II\quad& 36a + 6b &=& 0 \\ \end{array}$

Dieses Gleichungssystem lösen wir mit dem Einsetzungsverfahren:

Als erstes stellen wir Gleichung $I$ nach $a$ um und erhalten

$\begin{array}{rlll} &I\quad& a = 25 - b \\ \end{array}$

Setzen wir diese (umgeformte) Gleichung $I$ in Gleichung $II$ ein, erhalten wir

$\begin{array}{rlll} &II\quad&&& 36a + 6b &=& 0 &\mid a = 25 - b \, \textrm{einsetzen} \\ &&&\Rightarrow& 36 \cdot (25 - b) + 6b &=& 0 &\mid \textrm{Ausmultiplizieren} \\ &&&\Rightarrow& 900 - 36b + 6b &=& 0 \\ &&&\Rightarrow& 900 - 30b &=& 0 &\mid + 30b \\ &&&\Rightarrow& 30b &=& 900 &\mid : 30 \\ &&&\Rightarrow& b &=& 30 \\ \end{array}$

Setzen wir $b = 30$ in die (umgeformte) Gleichung $I$ ein, erhalten wir

$\begin{array}{rlll} &I&&& a &=& 25 - b &\mid b = 30 \, \textrm{einsetzen} \\ &&&\Rightarrow& a &=& 25 - 30 \\ &&&\Rightarrow& a &=& -5 \\ \end{array}$

und damit insgesamt

$f(t) = -5t^2 + 30t$

b)

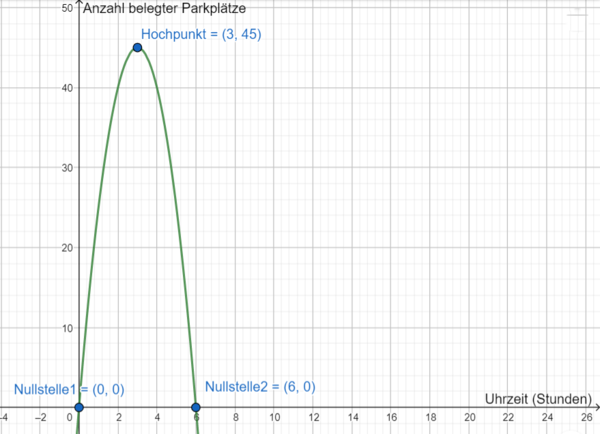
Entscheide, ob die 50 Parkplätze für die gesamte Dauer des Elternsprechtages ausreichend sind oder zusätzliche Parkplätze angemietet werden müssen.

Damit die Parkplätze ausreichen, dürfen maximal 50 Parkplätze zu einer bestimmten Uhrzeit belegt sein. Hat die Funktion einen Hochpunkt mit einem Funktionswert kleiner gleich 50, so ist sie nirgendwo größer als dort.

$\begin{array}{rlll} &\textrm{notwendige} \, \textrm{Bedingung:}& f'(t) &=& 0 \\ &\textrm{hinreichende} \, \textrm{Bedingung:}& f''(t) &<& 0 \\ \end{array}$

Der Graph der Funktion $f$ hat den Hochpunkt $(3 | 45)$. Die maximale Anzahl belegter Parkplätze ist also um 15 Uhr nachzuweisen. Zu der Zeit sind 45 Parkplätze belegt, sodass die vorhandenen 50 Parkplätze ausreichen.

$\begin{array}{rlll} f(t) &=& -5t^2 + 30t \\ f'(t) &=& -10t + 30 \\ f''(t) &=& -10 \\ \end{array}$

$\begin{array}{rlll} \textrm{Notwendige Bedingung:} && f'(t) &=& 0 \\ &\Leftrightarrow& -10t + 30 &=& 0 &\mid + 10t\\ &\Leftrightarrow& 10t &=& 30 &\mid : 10 \\ &\Leftrightarrow& t &=& 3 \\ \end{array}$



$\begin{array}{rlll} \textrm{Hinreichende Bedingung:} &&f'(3) &=& 0 &&\textrm{und} \\ &&f''(3) &=& -10 &<& 0 \end{array}$

$f(3)=-5 \cdot 3^2 + 30 \cdot 3 = 45$

c)

Skizziere nun den Graphen von $f$ anhand der Informationen auf einem Blatt. Beachte hierbei die geeignete Beschriftung der Koordinatenachsen. Für welchen Zeitraum ist dieser Graph als mathematische Modellierung der Parkplatzsituation geeignet?

Da die Funktionswerte von $f$ für $t < 0$ und $t > 6$ negativ sind, ist der Graph nur für $0 \leq t \leq 6$ als mathematische Modellierung der Parkplatzsituation geeignet.

Das Gauß-Verfahren

Das Gauß-Verfahren

Das Gauß-Verfahren verwendest du bei Gleichungssystemen mit 2 oder mehr Variablen. Dabei versuchst du die Gleichungen so zu vereinfachen, das eine obere Dreiecksmatix entsteht.

Schaue dir folgende Gleichungen an:

$\begin{array}{rlll} &I\quad& &3x& + &5y& + &4z& &=& &6&\\ &II\quad& &2x& + &1y& + &7z& &=& &15& \\ &III\quad& &1x& + &2y& + &3z& &=& &5& \\ \end{array}$

In Matrix-Vektor-Schreibweise sieht das so aus:

$\begin{pmatrix} 3 & 5 & 4& 6 \\ 2 & 1 & 7 & 15 \\ 1 & 2 & 3 & 5\end{pmatrix}$

1. Um die $x$-Variable in Gleichung $II$ zu eliminieren rechnen wir $II + (-2) \cdot III$:

$\begin{array}{rlll} &I\quad& &3x& + &5y& + &4z& &=& &6&\\ &II\quad& && - &3y& + &1z& &=& &5& \\ &III\quad& &1x& + &2y& + &3z& &=& &5& \\ \end{array}$

In Matrix-Vektor-Schreibweise:

$\begin{pmatrix} 3 & 5 & 4& 6 \\ 0 & -3 & 1 & 15 \\ 1 & 2 & 3 & 5\end{pmatrix}$

2. Um die $x$-Variable in Gleichung $III$ zu eliminieren rechnen wir $III \cdot (-3) + I$:

$\begin{array}{rlll} &I\quad& &3x& + &5y& + &4z& &=& &6&\\ &II\quad& && - &3y& + &1z& &=& &5& \\ &III\quad& && - &1y& - &5z& &=& &-9& \\ \end{array}$

In Matrix-Vektor-Schreibweise:

$\begin{pmatrix} 3 & 5 & 4& 6 \\ 0 & -3 & 1 & 15 \\ 0 & -1 & -5 & -9\end{pmatrix}$

3. Nun soll auch die $y$-Variable in Gleichung $III$ eliminiert werden. Dazu rechnen wir $III \cdot (-3) + II$

Unsere Gleichungen sehen nun folgendermaßen aus:

$\begin{array}{rlll} &I\quad& &3x& + &5y& + &4z& &=& &6&\\ &II\quad& && - &3y& + &1z& &=& &5& \\ &III\quad& && && + &16z& &=& &32& \\ \end{array}$

In Matrix-Vektor-Schreibweise:

$\begin{pmatrix} 3 & 5 & 4& 6 \\ 0 & -3 & 1 & 15 \\ 0 & 0 & 16 & 32\end{pmatrix}$

Wir können Gleichung $III$ nun nach $z$ auflösen. Dann setzen wir den $z$-Wert in Gleichung $II$ ein und lösen nach $y$ auf. Zuletzt setzten wir jeweils den berechneten $y$- und $z$-Wert in Gleichung $I$ ein und lösen nach $x$ auf. Wir erhalten so unsere dritte Variable.

Es folgt also:

$z=2$, $y=-1$, $x=1$

Merke

Du verwendest dieses Verfahren bei Gleichungssystemen mit 2 oder mehr Variablen. Dabei stellst du die Gleichungen so um, das in einer Gleichung nur eine Variable, in der zweiten Gleichung zwei Variablen und in der dritten Gleichung alle drei Variablen vorkommen. Das bezeichnet man auch als obere Dreiecksmatrix. Nun kannst du mit der ersten Gleichung so vorgehen wie bei einer Gleichung mit nur einer Variable und die Lösung dann in die zweite Gleichung einsetzen. Die Lösung dieser Gleichung setzt du dann in die letzte Gleichung ein. Bei vier Gleichungen mit vier Variablen gehst du analog vor.

Aufgaben zum Gauß-Verfahren

Gleichungssysteme lösen.

Die Schwierigkeit der Aufgaben steigt von oben nach unten.

a)

$\begin{array}{rlll} &I\quad& &1x& + &12y& + &6z& &=& &-2&\\ &II\quad& &-2x& + &7y& + &18z& &=& &24,5& \\ &III\quad& &4x& + &2y& + &24z& &=& &-31& \\ \end{array}$

Schreibe die Gleichungen in die Matrix-Vektor-Schreibweise um.

Eliminiere zuerst die $x$-Variable in der zweiten Zeile.

Deine Matrix sollte in folgende Form umgeschrieben werden. $\begin{pmatrix} a & b & c & d \\ 0 & e & f & g \\ 0 & 0 & h & i \end{pmatrix}$.

$x=-9$,$y=7$, $z=1/6$

b)*

$\begin{array}{rlll} &I\quad& &3x& + &4y& - &5z& + &6v& &=& &-7,5&\\ &II\quad& &6x& + &5y& - &6z& + &5v& &=& &-7,5& \\ &III\quad& &9x& - &4y& + &2z& + &3v& &=& &69& \\ &IV\quad& && &2y& - &3z& + &1v& &=& &-14,5& \end{array}$

Schreibe die Gleichungen in die Matrix-Vektor-Schreibweise um.

Eliminiere zuerst den $x$-Wert in Gleichung $II$.

Die Matrix sollte in eine obere rechte Dreiecksmatrix umgeschrieben werden.

$x=3,5$,$y=-7$, $z=1$, $v=2,5$

Kubische Funktionen im Sachzusammenhang

Aufgabe: Virusinfektion

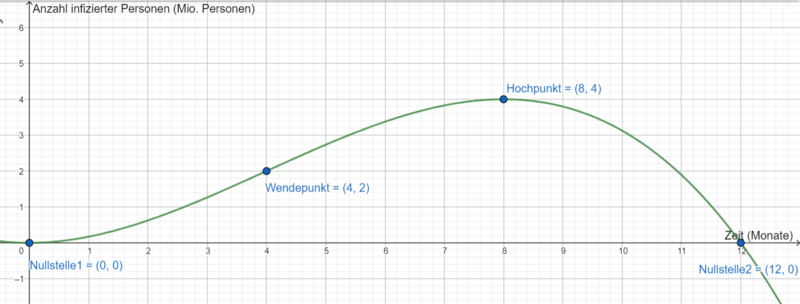
Im Januar befällt ein neuartiges Virus Deutschland. Mittlerweile ist es Oktober und du suchst im Internet nach Informationen über die Infektionszahlen. Dort triffst du auf folgende Informationen:

• Im Dezember des Vorjahres befinden sich noch keine infizierten Personen in Deutschland
• Im April leben 2.000.000 infizierte Personen in Deutschland
• Im August leben 4.000.000 infizierte Personen in Deutschland
• Durch entsprechende Maßnahmen ist die Zahl infizierter Personen ab August rückläufig

a)

Die Anzahl infizierter Personen lässt sich durch eine kubische Funktion der Form $f(t) = at^3 + bt^2 + ct + d$ beschreiben. Stelle die Gleichung von $f$ auf. Löse zunächst unteren Lückentext und stelle dann mit dessen Hilfe die Gleichung von $f$ auf. Indem du die Box "Funktionsgleichung überprüfen" öffnest, kannst du dein Ergebnis selbstständig überprüfen.

$f(t) = -\frac{1}{64} t^3 + \frac{3}{16} t^2 = \frac{1}{64} (-t^3 + 12t^2)$

$\begin{array}{rlll} f(t) &=& at^3 + bt^2 + ct + d \\ f'(t) &=& 3at^2 + 2bt + c \\ \end{array}$



$\begin{array}{rlll} &&f(0) &=& 0 \\ &\Leftrightarrow& a \cdot 0^3 + b \cdot 0^2 + c \cdot 0 + d &=& 0 \\ &\Leftrightarrow& d &=& 0 \\ \end{array}$



$\Rightarrow f(t) = at^3 + bt^2 + ct$



$\begin{array}{rlll} &&f(4) &=& 2 \\ &\Leftrightarrow& a \cdot 4^3 + b \cdot 4^2 + c \cdot 4 &=& 2 \\ &\Leftrightarrow& 64a + 16b + 4c &=& 2 \\ \end{array}$



$\begin{array}{rlll} &&f(8) &=& 4 \\ &\Leftrightarrow& a \cdot 8^3 + b \cdot 8^2 + c \cdot 8 &=& 4 \\ &\Leftrightarrow& 512a + 64b + 8c &=& 4 \\ \end{array}$



$\begin{array}{rlll} &&f'(8) &=& 0 \\ &\Leftrightarrow& 3a \cdot 8^2 + 2b \cdot 8 + c &=& 0 \\ &\Leftrightarrow& 192a + 16b + c &=& 0 \\ \end{array}$





Insgesamt erhalten wir also folgendes Gleichungssystem:

$\begin{array}{rlll} &I\quad& &64a& + &16b& + &4c& &=& &2& \\ &II\quad& &512a& + &64b& + &8c& &=& &4& \\ &III\quad& &192a& + &16b& + &1c& &=& &0& \\ \end{array}$

Dieses Gleichungssystem lösen wir mit dem Gauß-Verfahren:

$II - 8 \cdot I$

$\begin{array}{rlll} &I\quad& &64a& + &16b& + &4c& &=& &2& \\ &II\quad& && - &64b& - &24c& &=& &-12& \\ &III\quad& &192a& + &16b& + &1c& &=& &0& \\ \end{array}$



$III - 3 \cdot I$

$\begin{array}{rlll} &I\quad& &64a& + &16b& + &4c& &=& &2& \\ &II\quad& && - &64b& - &24c& &=& &-12& \\ &III\quad& && - &32b& - &11c& &=& &-6& \\ \end{array}$



$III - \frac{1}{2} \cdot II$

$\begin{array}{rlll} &I\quad& &64a& + &16b& + &4c& &=& &2& \\ &II\quad& && - &64b& - &24c& &=& &-12& \\ &III\quad& && && &21c& &=& &0& \\ \end{array}$



Gleichung $III$ liefert uns nun

$\begin{array}{rlll} &III\quad&&& 21c &=& 0 &\mid : 21 \\ &&&\Rightarrow& c &=& 0 \\ \end{array}$

Setzen wir $c = 0$ in Gleichung $II$ ein, erhalten wir

$\begin{array}{rlll} &II\quad&&& -64b + 24c &=& -12 &\mid c = 0 \, \textrm{einsetzen} \\ &&&\Rightarrow& -64b + 24 \cdot 0 &=& -12 \\ &&&\Rightarrow& -64b &=& -12 &\mid : (-64) \\ &&&\Rightarrow& b &=& \frac{3}{16} \\ \end{array}$

Setzen wir $c = 0$ und $b = \frac{3}{16}$ in Gleichung $I$ ein, erhalten wir

$\begin{array}{rlll} &I\quad&&& 64a + 16b + 4c &=& 2 &\mid c = 0 \, \textrm{und} \, b = \frac{3}{16} \, \textrm{einsetzen}\\ &&&\Rightarrow& 64a + 16 \cdot \frac{3}{16} + 4 \cdot 0 &=& 2 \\ &&&\Rightarrow& 64a + 3 &=& 2 &\mid -3 \\ &&&\Rightarrow& 64a &=& -1 &\mid : 64 \\ &&&\Rightarrow& a &=& -\frac{1}{64} \\ \end{array}$



und damit insgesamt

$f(t) = -\frac{1}{64} t^3 + \frac{3}{16} t^2 = \frac{1}{64} (-t^3 + 12t^2)$

b)

Forscher gehen nun (im Oktober) davon aus, dass noch im selben Jahr alle jemals infizierten Personen in Deutschland geheilt sind und entsprechend keine Fälle mehr in Deutschland auftreten. Prüfe diese Vorhersage anhand der Informationen.

Zu den Zeitpunkten, zu denen keine infizierten Personen in Deutschland leben, hat der Graph seine Nullstellen.

Gleichungen, die nur Summanden mit der Variable $t$ enthalten, lassen sich durch Faktorisieren lösen .

$f$ hat Nullstellen bei $t_{1} = 0$ und $t_{2} = 12$. Im Dezember treten also keine infizierten Fälle mehr in Deutschland auf, sodass alle jemals infizierten Personen in Deutschland noch im selben Jahr geheilt sind. Die Vorhersage ist demnach richtig.

$\begin{array}{rlll} &&f(t) &=& 0 \\ &\Leftrightarrow& \frac{1}{64} (-t^3 + 12t^2) &=& 0 &\mid :\frac{1}{64} \\ &\Leftrightarrow& -t^3 + 12t^2 &=& 0 &\mid \textrm{Faktorisieren} \\ &\Leftrightarrow& t^2 (-t + 12) &=& 0 \\ &\Rightarrow& t^2 = 0 & \textrm{und}& && -t + 12 &=& 0 \\ &\Leftrightarrow& t_{1} = 0 & \textrm{und}& && t_{2} &=& 12 \\ \end{array}$

c)

Forscher behaupten weiterhin, dass die milden Temperaturen im Frühling dafür sorgen, dass sich der temperaturempfindliche Virus optimal ausbreiten kann und deshalb die stärkste Zunahme infizierter Personen im Frühling nachzuweisen ist. Prüfe diese Behauptung anhand der Informationen.

Der Wendepunkt ist der Punkt der stärksten Zunahme (oder stärksten Abnahme) des Funktionsgraphen, der an dieser Stelle sein Krümmungsverhalten ändert.

$\begin{array}{rlll} &\textrm{notwendige} \, \textrm{Bedingung:}& f''(t) &=& 0 \\ &\textrm{hinreichende} \, \textrm{Bedingung:}& f'''(t) &\neq& 0 \\ \end{array}$

Der Graph der Funktion $f$ hat einen Wendepunkt bei $t = 4$. Die stärkste Zunahme infizierter Personen ist also im April (bzw. im Frühling) nachzuweisen. Die Behauptung ist demnach richtig.

$\begin{array}{rlll} f(t) &=& -\frac{1}{64} t^3 + \frac{3}{16} t^2 \\ f'(t) &=& -\frac{3}{64} t^2 + \frac{3}{8} t \\ f''(t) &=& -\frac{3}{32} t + \frac{3}{8} \\ f'''(t) &=& -\frac{3}{32} \\ \end{array}$

$\begin{array}{rlll} \textrm{Notwendige} \, \textrm{Bedingung:} && f''(t) &=& 0 \\ &\Leftrightarrow& -\frac{3}{32} t + \frac{3}{8} &=& 0 &\mid +\frac{3}{32} t\\ &\Leftrightarrow& \frac{3}{32} t &=& \frac{3}{8} &\mid :\frac{3}{32} \\ &\Leftrightarrow& t &=& 4 \\ \end{array}$

$\begin{array}{rlll} \textrm{Hinreichende} \, \textrm{Bedingung:} &&f''(4) &=& 0 &&\textrm{und} \\ &&f'''(4) &=& -\frac{3}{32} &\neq& 0 \end{array}$

d)

Skizziere nun den Graphen von $f$ anhand der Informationen auf einem Blatt. Beachte hierbei die geeignete Beschriftung der Koordinatenachsen. Für welchen Zeitraum ist dieser Graph als mathematische Modellierung der Virusinfektion geeignet?

Da die Funktionswerte von $f$ für $t > 12$ negativ sind, ist der Graph nur für $0 \leq t \leq 12$ als mathematische Modellierung der Virusinfektion geeignet. Inwiefern der Graph für das vorherige Jahr geeignet ist, lässt sich anhand der Informationen nicht eindeutig feststellen. Der Graph zeigt jedoch, dass zu einem bestimmten Zeitpunkt vor dem beobachteten Jahr unendlich viele infizierte Personen in Deutschland leben, was offensichtlich nicht möglich ist.

Alles klar?

Bearbeite den Lückentext