Digitale Werkzeuge in der Schule/Basiswissen Analysis/Optimierungsprobleme: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung |
|||
| Zeile 191: | Zeile 191: | ||
|Icon= {{Vorlage:Icon pencil}} | |Icon= {{Vorlage:Icon pencil}} | ||
}} | }} | ||
{{Lösung versteckt|1= | |||
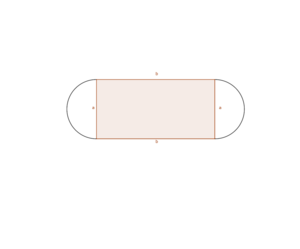
Den Flächeninhalt berechnen wir mit der Funktion <math>A(x,y)=x*y</math>. | |||
Die Nebenbedingung ist die angegebene Funktion <math>f(x)=f(x)=(x-3)^2+2,5</math>. | |||
Setzt man nun die Nebenbedingung in die Funktion ein, die die Flächeninhalt errechnet, so erhalten wir die neue Funktion <math>A(x)=x^3-6x^2+11x</math>. | |||
Die Funktion A hängt also nur noch von der Unbekannten x ab. | |||
Nun lässt sich mit Hilfe der notwendigen Bedingung <math>A'(x)=0</math> und der hinreichenden Bedingung für Hochpunkte <math>A''(x) < 0 </math> die Stelle des lokalen Hochpunktes bestimmen. Anschließend setzen wir den x Wert in die Ausgangsfunktion A(x) ein und erhalten nun den lokalen Hochpunkt (1,59,7,14). | |||
Zuletzt prüfen wir noch die Randpunkte. | |||
A(0) | |||
|2=Lösung |3=Lösung verbergen }} | |||
==Optimierungsprobleme & Funktionenscharen== | ==Optimierungsprobleme & Funktionenscharen== | ||
Version vom 30. April 2020, 09:04 Uhr
Allgemeine Hinweise
Einführung: Optimierungsprobleme
Vorgehen beim Lösen von Optimierungsproblemen
Globales Extremum und Randextremum
Den Flächeninhalt berechnen wir mit der Funktion . Die Nebenbedingung ist die angegebene Funktion . Setzt man nun die Nebenbedingung in die Funktion ein, die die Flächeninhalt errechnet, so erhalten wir die neue Funktion . Die Funktion A hängt also nur noch von der Unbekannten x ab. Nun lässt sich mit Hilfe der notwendigen Bedingung und der hinreichenden Bedingung für Hochpunkte die Stelle des lokalen Hochpunktes bestimmen. Anschließend setzen wir den x Wert in die Ausgangsfunktion A(x) ein und erhalten nun den lokalen Hochpunkt (1,59,7,14). Zuletzt prüfen wir noch die Randpunkte.
A(0)Optimierungsprobleme & Funktionenscharen