Digitale Werkzeuge in der Schule/Basiswissen Analysis/Optimierungsprobleme: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung |
||
| Zeile 58: | Zeile 58: | ||
}} | }} | ||
{{Box-spezial | |||
{{Box | |Titel= <span style="color: {{Farbe|orange}}">Beispiel: Aufgabe 1</span> | ||
| | |Inhalt= | ||
| | |||
Ein Sportplatz mit einer 400-m-Laufbahn soll so angelegt werden, dass das Fußballfeld möglichst groß ist. | Ein Sportplatz mit einer 400-m-Laufbahn soll so angelegt werden, dass das Fußballfeld möglichst groß ist. | ||
| Zeile 69: | Zeile 68: | ||
'''b)''' Wie groß ist das Fussballfeld? | '''b)''' Wie groß ist das Fussballfeld? | ||
|Farbe= {{Farbe|orange}} | |||
|Icon= {{Vorlage:Icon pencil}} | |||
}} | |||
{{Lösung versteckt | {{Lösung versteckt | ||
| Zeile 116: | Zeile 120: | ||
}} | }} | ||
|3=Merke | <nowiki>|3=Merke | ||
}} | }}</nowiki> | ||
Version vom 29. April 2020, 14:46 Uhr
Allgemeine Hinweise
Einführung: Optimierungsprobleme
Vorgehen beim Lösen von Optimierungsproblemen
Schritt 1:
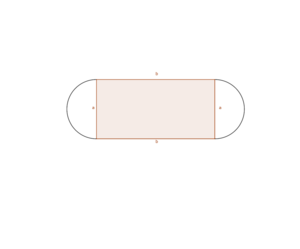
Gegeben ist die Länge der Laufbahn um den Sportplatz herum, also der Umfang des Sportplatzes. Maximiert werden soll die Größe des Fussballfeldes, also der rechteckige Flächeninhalt innerhalb des Sportplatzes.
Erstelle eine Skizze dazu.
Schritt 2:
Die Formel zum Flächeninhalt ist . Dies ist deine Hauptbedingung.
Deine Nebenbedingung findest du im Umfang wieder: . Diese kannst du nach a umstellen und erhälst:
Setze nun deine Nebenbedingung in deine Hauptbedigung ein und erhalte die Zielfunktion:
.
Für diese Funktion kann b nur zwischen 0 und 200 liegen, also
Schritt 3:
Berechne nun deinen Extremwert. Bilde dazu die Ableitungen:
Mit der notwendigen Bedingung erhälst du dann . Mit der hinreichenden Bedindung folgt , somit erfüllt alle Bedingungen.
Berechne nun und den Flächeninhalt:
- und
a) Der Flächeninhalt des Fussballfeldes wird für eine Breite von und eine Höhe von maximal.
b) Der Flächeninhalt wird auf maximiert.|3=Merke }}
Globales Extremum und Randextremum
Optimierungsprobleme & Funktionenscharen
Die zu optimierende Größe ist der Funktionswert am Tiefpunkt der Funktion.
Berechne also zunächst den Tiefpunkt der Funktion in Abhängigkeit von t.
Ableiten der Funktion ergibt:
Für ein Minimum muss gelten: und .
Minimum
Setze nun in ein, um den Funktionswert am Minimum zu bestimmen:
Bezeichnen wir den Funktionswert am Tiefpunkt mit einer neuen Gleichung , so ergibt sich also:
Die zu optimierende Größe ist der Funktionswert am Tiefpunkt der Funktion.
Berechne also zunächst den Tiefpunkt der Funktion in Abhängigkeit von t:
Ableiten der Funktion ergibt:
Für ein Minimum muss gelten: und .
Minimum
Setze nun in ein, um den Funktionswert am Minimum zu bestimmen:
Bezeichnen wir den Funktionswert am Tiefpunkt mit einer neuen Gleichung , so ergibt sich also:
.
Gesucht ist das , für das der Funktionswert maximal ist, also das Maximum der Funktion .
Bilde zunächst wieder die Ableitungen und :
Bei einem Maximum muss gelten: und .
Maximum
Der Funktionswert des Tiefpunktes ist also für maximal.