Digitale Werkzeuge in der Schule/Basiswissen Analysis/Optimierungsprobleme: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 111: | Zeile 111: | ||
|2= Lösung | |2= Lösung | ||
|1= | |1= | ||
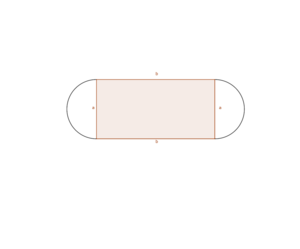
'''a)''' Der Flächeninhalt des Fussballfeldes wird für eine Breite von <math>63,66m</math> und eine Höhe von <math>100m</math> maximal | '''a)''' Der Flächeninhalt des Fussballfeldes wird für eine Breite von <math>63,66m</math> und eine Höhe von <math>100m</math> maximal. | ||
'''b)''' Der Flächeninhalt wird auf <math> 6366 m </math> maximiert. | '''b)''' Der Flächeninhalt wird auf <math> 6366 m </math> maximiert. | ||
Version vom 29. April 2020, 14:43 Uhr
Allgemeine Hinweise
Einführung: Optimierungsprobleme
Vorgehen beim Lösen von Optimierungsproblemen
Globales Extremum und Randextremum
Optimierungsprobleme & Funktionenscharen
Die zu optimierende Größe ist der Funktionswert am Tiefpunkt der Funktion.
Berechne also zunächst den Tiefpunkt der Funktion in Abhängigkeit von t.
Ableiten der Funktion ergibt:
Für ein Minimum muss gelten: und .
Minimum
Setze nun in ein, um den Funktionswert am Minimum zu bestimmen:
Bezeichnen wir den Funktionswert am Tiefpunkt mit einer neuen Gleichung , so ergibt sich also:
Die zu optimierende Größe ist der Funktionswert am Tiefpunkt der Funktion.
Berechne also zunächst den Tiefpunkt der Funktion in Abhängigkeit von t:
Ableiten der Funktion ergibt:
Für ein Minimum muss gelten: und .
Minimum
Setze nun in ein, um den Funktionswert am Minimum zu bestimmen:
Bezeichnen wir den Funktionswert am Tiefpunkt mit einer neuen Gleichung , so ergibt sich also:
.
Gesucht ist das , für das der Funktionswert maximal ist, also das Maximum der Funktion .
Bilde zunächst wieder die Ableitungen und :
Bei einem Maximum muss gelten: und .
Maximum
Der Funktionswert des Tiefpunktes ist also für maximal.