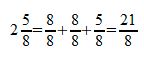Julius-Echter-Gymnasium/Mathematik/Addition und Subtraktion von gemischten Zahlen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 62: | Zeile 62: | ||
'''Übungen zur Subtraktion von gemischten Zahlen:''' | '''Übungen zur Subtraktion von gemischten Zahlen:''' | ||
{{Box|Aufgabe 1|{{LearningApp|app=pn2451bma18|width=100%|height= | {{Box|Aufgabe 1|{{LearningApp|app=pn2451bma18|width=100%|height=900px}}|Üben}} | ||
{{Box|Aufgabe 2|{{LearningApp|app=p6d3ebek518|width=100%|height=500px}}|Üben}} | {{Box|Aufgabe 2|{{LearningApp|app=p6d3ebek518|width=100%|height=500px}}|Üben}} | ||
{{Box|Aufgabe 3|{{LearningApp|app=pvqbscw8j18|width=100%|height= | {{Box|Aufgabe 3|{{LearningApp|app=pvqbscw8j18|width=100%|height=300px}}|Üben}} | ||
Version vom 4. Februar 2020, 11:12 Uhr
Bei der Addition und Subtraktion von gemischten Zahlen ist es wichtig, die gemischte Zahl zunächst in einen normalen Bruch umzuwandeln, wie folgendes Beispiel zeigt:
Übe zunächst das Umwandeln der gemischten Zahlen vor dem Addieren und Subtrahieren:
Übungen zur Addition von gemischten Zahlen:
Übungen zur Subtraktion von gemischten Zahlen: