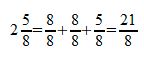Julius-Echter-Gymnasium/Mathematik/Addition und Subtraktion von gemischten Zahlen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
K (40 Versionen importiert) |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 1: | Zeile 1: | ||
< | {{Box|Gemischte Zahlen|Gemischte Zahlen sind solche Brüche, bei denen eine ganze Zahl vor dem Bruch steht. Zum Beispiel: <math> 2 \frac{5}{8}</math> "Zwei Ganze Fünf Achtel"|Kurzinfo}} | ||
Bei der Addition und Subtraktion von '''gemischten Zahlen''' ist es wichtig, die gemischte Zahl zunächst in einen '''normalen Bruch''' umzuwandeln | Bei der Addition und Subtraktion von '''gemischten Zahlen''' ist es wichtig, die gemischte Zahl zunächst in einen '''normalen Bruch''' umzuwandeln, wie folgendes Beispiel zeigt: | ||
[[Datei: | [[Datei:Gemischte Zahl.jpg|links|Umwandeln einer gemischten Zahl in einen Bruch]] | ||
<br /> | |||
<br /> | |||
<br /> | |||
<br /> | |||
<br /> | |||
{{Box|Erklärung:|Alle gemischten Zahlen, mit denen addiert oder subtrahiert wird, müssen zunächst nach diesem Beispiel in einen normalen Bruch umgewandelt werden. | |||
Man betrachtet den Nenner des Bruches (in diesem Fall eine 8) und wandelt die '''ganze Zahl''', die vor dem Bruch steht (in diesem Fall eine 2), in Brüche mit dem '''gleichen Nenner''' um. | |||
<math> \frac{8}{8}</math> entspricht einer 1. Da vor dem Bruch allerdings eine '''2''' als ganze Zahl steht, muss der Bruch <math> \frac{8}{8}</math> auch '''zwei-mal''' vorkommen. | |||
Zu der in Brüche umgewandelten 2 wird nun noch der ursprüngliche Bruch <math> \frac{5}{8}</math> dazu genommen. | |||
Alle Brüche haben nun den '''gleichen Nenner'''. <br /> | |||
Somit können jetzt die '''Zähler''' addiert und die drei Brüche zu einem Bruch zusammengefasst werden.|Unterrichtsidee }} | |||
{{Box|Beispiel|Nun wird ein konkretes Beispiel einer Addition von gemischten Zahlen betrachtet:|Arbeitsmethode}} | |||
[[Datei: | [[Datei:Gemischte Zahlen addieren.jpg|zentriert|Addieren von zwei gemischten Zahlen]] | ||
<br /> | |||
<br /> | |||
<br /> | |||
''' | '''Übe zunächst das Umwandeln der gemischten Zahlen vor dem Addieren und Subtrahieren:''' | ||
{{Box|Übung|{{LearningApp|app=p4ifs9nb318|width=100%|height=500px}}|Üben}} | |||
{{Box|1=Beachte:|2=In den nachfolgenden Aufgaben werden die Brüche mit Schrägstrich (Bsp: <math> \frac{2}{3}</math> = 2/3) dargestellt. | |||
|3=Hervorhebung1}} | |||
'''Übungen zur Addition von gemischten Zahlen:''' | |||
{{Box|Aufgabe 1|{{LearningApp|app=pyeiii50k18|width=100%|height=500px}}|Üben}} | |||
{{Box|Aufgabe 2|{{LearningApp|app=pyn950oga18|width=100%|height=500px}}|Üben}} | |||
{{Box|Aufgabe 3|{{LearningApp|app=pcjgf4mak18|width=100%|height=500px}}|Üben}} | |||
'''Übungen zur Subtraktion von gemischten Zahlen:''' | |||
{{Box|Aufgabe 1|{{LearningApp|app=pn2451bma18|width=100%|height=500px}}|Üben}} | |||
{{Box|Aufgabe 2|{{LearningApp|app=p6d3ebek518|width=100%|height=500px}}|Üben}} | |||
{{Box|Aufgabe 3|{{LearningApp|app=pvqbscw8j18|width=100%|height=500px}}|Üben}} | |||
{{Fortsetzung|weiter=Addition und Subtraktion von Dezimalzahlen|weiterlink=Julius-Echter-Gymnasium/Mathematik/Addition_und_Subtraktion_von_Dezimalzahlen|vorher=Addition und Subtraktion ungleichnamiger Brüche|vorherlink=Julius-Echter-Gymnasium/Mathematik/Addition_und_Subtraktion_ungleichnamiger_Brüche}} | |||
{{SORTIERUNG:{{SUBPAGENAME}}}} | |||
[[Kategorie:Julius-Echter-Gymnasium Mathematik]] | |||
{{ | |||
Version vom 4. Februar 2020, 11:10 Uhr
Bei der Addition und Subtraktion von gemischten Zahlen ist es wichtig, die gemischte Zahl zunächst in einen normalen Bruch umzuwandeln, wie folgendes Beispiel zeigt:
Übe zunächst das Umwandeln der gemischten Zahlen vor dem Addieren und Subtrahieren:
Übungen zur Addition von gemischten Zahlen:
Übungen zur Subtraktion von gemischten Zahlen: